Capítulo 4 Descrevendo variáveis quantitativas
Variáveis quantitativas podem ser discretas ou contínuas. A descrição dos padrões de distribuição destes tipos de variáveis é feita utilizando tabelas (frequência e frequência acumulada) e gráficos (histogramas ou gráficos de frequência acumulada).
4.1 Tabelas de frequência para variáveis quantitativas
A construção de tabelas de frequências para variáveis quantitativas necessita que agrupemos as observações em faixas de valores. Veja as observações abaixo por exemplo:
\(X =\) {2.66, 3.72, 5.73, 9.08, 2.02, 8.98, 9.45, 6.61, 6.29, 0.62}
Podemos agrupá-las nas seguintes faixas de valores:
(0,2], (2,4], (4,6], (6,8], (8,10]
Estas faixas de valores são denominadas de intervalos de classe. Se alocadas nestes intervalos, as observações ficam:
| X | Classes |
|---|---|
| 2.66 | (2,4] |
| 3.72 | (2,4] |
| 5.73 | (4,6] |
| 9.08 | (8,10] |
| 2.02 | (2,4] |
| 8.98 | (8,10] |
| 9.45 | (8,10] |
| 6.61 | (6,8] |
| 6.29 | (6,8] |
| 0.62 | (0,2] |
Uma tabela de frequência para estas observações é construínda contando o número de observações por intervalo de classes. Neste caso:
| Classes | Frequencia |
|---|---|
| (0,2] | 1 |
| (2,4] | 3 |
| (4,6] | 1 |
| (6,8] | 2 |
| (8,10] | 3 |
Na coluna Frequencia temos o número de observações da variável X para cada um dos intervalos de classe.
4.1.1 Alterando o tamanho dos intervalos de classe
No exemplo anterior definimos os limites dos intervalos de classe de 2 em 2 unidades. Poderíamos ter escolhido outros tamanhos, por exemplo, de 4 em 4. Neste caso teríamos:
| Classes | Frequencia |
|---|---|
| (0,4] | 4 |
| (4,8] | 3 |
| (8,12] | 3 |
Note que ao escolhermos o tamanho dos intervalos de classe, estamos criando a variável qualitativa ordinal Classes, a partir do agrupamento das observações em X. Neste sentido, não há um único tamanho correto para os intervalos de classe. O objetivo é encontrar um tamanho que permita evidenciar os padrões de distribuição da variável sem perdermos muitos detalhes.
Poderíamos escolher um tamanho muito grande, de 5 em 5. Neste caso teríamos somente 2 grupos.
| Classes | Frequencia |
|---|---|
| (0,5] | 4 |
| (5,10] | 6 |
Por outro lado, poderíamos escolher um tamanho muito pequeno, por exemplo de 1 e 1.
| Classes | Frequencia |
|---|---|
| (0,1] | 1 |
| (2,3] | 2 |
| (3,4] | 1 |
| (5,6] | 1 |
| (6,7] | 2 |
| (8,9] | 1 |
| (9,10] | 2 |
Nas duas situações, não é possível evidenciar os padrões de distribuição da variável X. Na primeira, perdemos muita informação agrupando as observações em somente duas faixas e na última, perdemos a capacidade de visualizar os padrões de distribuição de X.
4.1.2 Tabela de frequência para CPUE
Carregue o pacote tidyverse e importe novamente a base de dados Reservatorios_Parana_parcial.csv.
# Carrega pacotes
library(tidyverse)
# Importa base de dados
res = read_delim('Reservatorios_Parana_parcial.csv',
delim = ',',
locale = locale(decimal_mark = '.',
encoding = 'latin1'))No objeto res temos 8 variáveis quantitativas: Fechamento, Area, pH, Condutividade, Alcalinidade, P.total, Riqueza, CPUE. Vamos verificar a como fica uma tabela de frequências para a variável CPUE que expressa a captura em \(kg\) de peixes em cada reservatório. Inicialmente, vamos selecionar somente esta coluna da tabela e visualizá-la em ordem crescente.
res %>%
select(CPUE) %>%
arrange(CPUE)| CPUE |
|---|
| 2.05 |
| 2.43 |
| 4.01 |
| 4.71 |
| 5.60 |
| 5.95 |
| 6.29 |
| 7.35 |
| 7.51 |
| 7.75 |
| 7.95 |
| 9.22 |
| 9.40 |
| 11.59 |
| 11.73 |
| 11.74 |
| 12.55 |
| 13.04 |
| 13.12 |
| 13.67 |
| 13.72 |
| 13.86 |
| 16.10 |
| 16.50 |
| 17.95 |
| 20.83 |
| 20.92 |
| 21.82 |
| 24.88 |
| 28.73 |
| 30.76 |
Vemos que o menor valor é 2.05 \(kg\) e o maior 30.76 \(kg\). Assumindo que temos 31 observações, vamos criar um intervalo de classes de 5 em 5 unidades. Para isto, criaremos a variável cl_cpue que será uma sequência de \(0\) a \(35\), com tamanho \(5\). Os valores nesta sequencia são os limites de classe
cl_cpue = seq(from = 0, to = 35, by = 5)
cl_cpue## [1] 0 5 10 15 20 25 30 35Utilizaremos os limites de classe para gerar uma nova coluna, delimitando os intervalos a que cada observação pertence. para isto utilizaremos a função cut.
tab_cpue = res %>%
select(CPUE) %>%
mutate(int_cpue = cut(CPUE, breaks = cl_cpue))
tab_cpue| CPUE | int_cpue |
|---|---|
| 9.22 | (5,10] |
| 28.73 | (25,30] |
| 11.59 | (10,15] |
| 30.76 | (30,35] |
| 5.95 | (5,10] |
| 7.75 | (5,10] |
| 7.51 | (5,10] |
| 4.01 | (0,5] |
| 20.83 | (20,25] |
| 2.43 | (0,5] |
| 12.55 | (10,15] |
| 11.73 | (10,15] |
| 13.72 | (10,15] |
| 16.50 | (15,20] |
| 4.71 | (0,5] |
| 7.95 | (5,10] |
| 13.12 | (10,15] |
| 16.10 | (15,20] |
| 11.74 | (10,15] |
| 17.95 | (15,20] |
| 13.86 | (10,15] |
| 13.04 | (10,15] |
| 7.35 | (5,10] |
| 20.92 | (20,25] |
| 13.67 | (10,15] |
| 21.82 | (20,25] |
| 6.29 | (5,10] |
| 9.40 | (5,10] |
| 5.60 | (5,10] |
| 2.05 | (0,5] |
| 24.88 | (20,25] |
A nova tabela tab_cpue tem agora duas colunas, os valores numéricos de CPUE e os valores transformados em intervalos de classe, int_cpue. É com esta última que montaremos a tabela de frequência.
fre_cpue = tab_cpue %>%
group_by(int_cpue) %>%
summarise(Frequencia = n())
fre_cpue| int_cpue | Frequencia |
|---|---|
| (0,5] | 4 |
| (5,10] | 9 |
| (10,15] | 9 |
| (15,20] | 3 |
| (20,25] | 4 |
| (25,30] | 1 |
| (30,35] | 1 |
e, em seguida de frequência relativa:
fre_cpue = fre_cpue %>%
mutate(Freq_relativa = Frequencia / sum(Frequencia))
fre_cpue| int_cpue | Frequencia | Freq_relativa |
|---|---|---|
| (0,5] | 4 | 0.1290323 |
| (5,10] | 9 | 0.2903226 |
| (10,15] | 9 | 0.2903226 |
| (15,20] | 3 | 0.0967742 |
| (20,25] | 4 | 0.1290323 |
| (25,30] | 1 | 0.0322581 |
| (30,35] | 1 | 0.0322581 |
Veja que os intervalos de (5,10] e (10,15] contém o maior número de observações, cerca de 29% cada um, e que acima de \(25\) \(kg\) temos somentes duas observações.
4.1.3 Tabela de frequência acumulada
Outra forma de representar o padrão de distribuição para uma variável quantitativa é apresentá-la em uma tabela de frequência acumulada. Fazemos isso, somando de forma cumulativa as observações em cada classe de intervalo e criando duas colunas adicionais de frequência acumulada e de frequência relativa acumulada.
fre_cpue = fre_cpue %>%
mutate(Freq_ac = cumsum(Frequencia),
Relativa_ac = cumsum(Freq_relativa))
fre_cpue| int_cpue | Frequencia | Freq_relativa | Freq_ac | Relativa_ac |
|---|---|---|---|---|
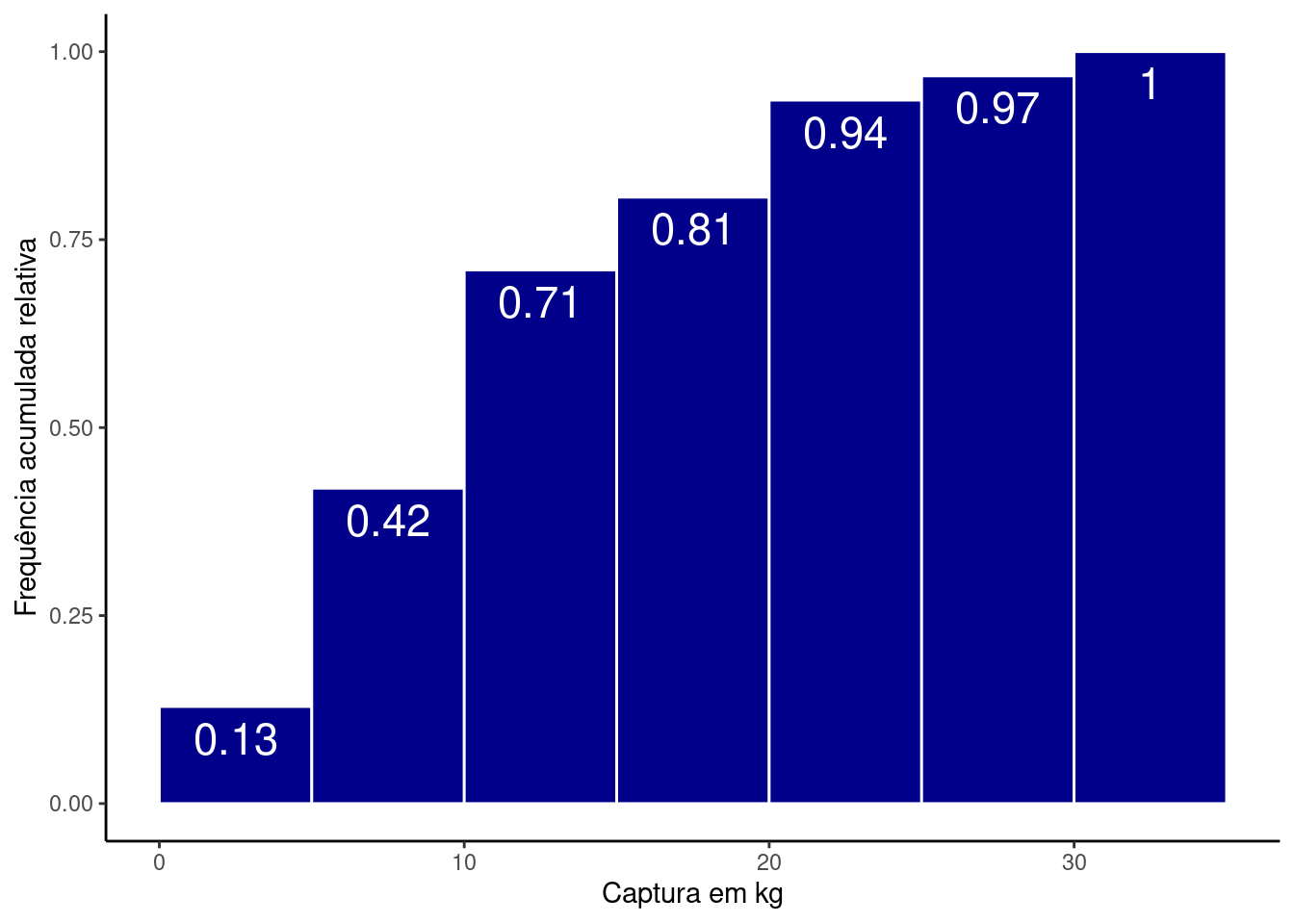
| (0,5] | 4 | 0.1290323 | 4 | 0.1290323 |
| (5,10] | 9 | 0.2903226 | 13 | 0.4193548 |
| (10,15] | 9 | 0.2903226 | 22 | 0.7096774 |
| (15,20] | 3 | 0.0967742 | 25 | 0.8064516 |
| (20,25] | 4 | 0.1290323 | 29 | 0.9354839 |
| (25,30] | 1 | 0.0322581 | 30 | 0.9677419 |
| (30,35] | 1 | 0.0322581 | 31 | 1.0000000 |
Veja agora que a última linha da coluna de frequência acumulada é igual ao número de observações total e que a da frequência relativa acumulada é igual a \(1\).
4.2 Representação gráfica: histogramas
Histogramas são regresentações das tabelas de frequência e de frequência relativa. Um histograma da coluna CPUE pode ser feito com o comando:
ggplot(res, aes(x = CPUE)) +
geom_histogram()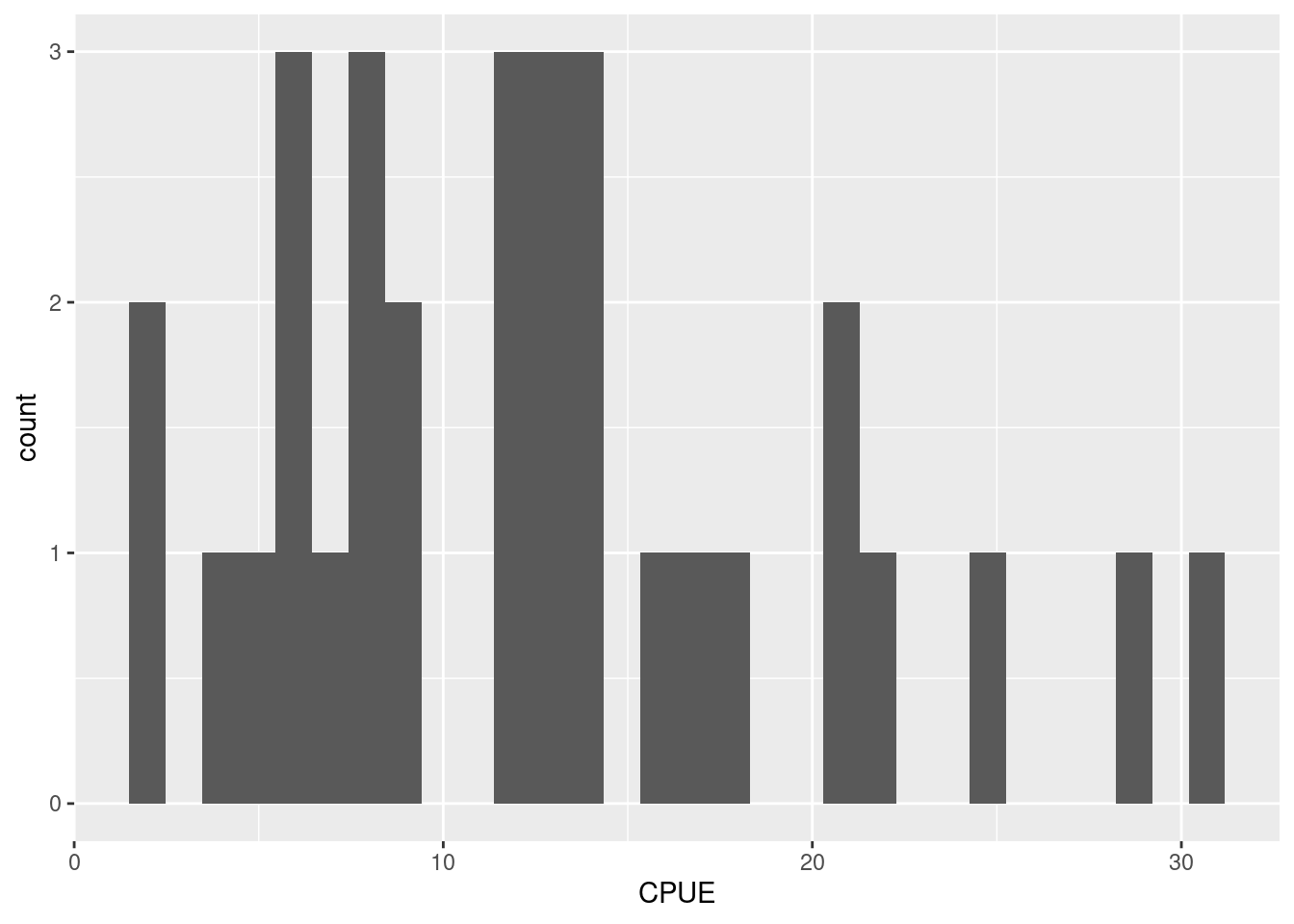
Os intervalos de classe foram escolhidos automaticamente pela função geom_histogram. Se quisermos ter o controle sobre estes intervalos, podemos adicionar o argumento beaks = e a sequência com os limites de classe que criamos anteriormente:
ggplot(res, aes(x = CPUE)) +
geom_histogram(breaks = cl_cpue)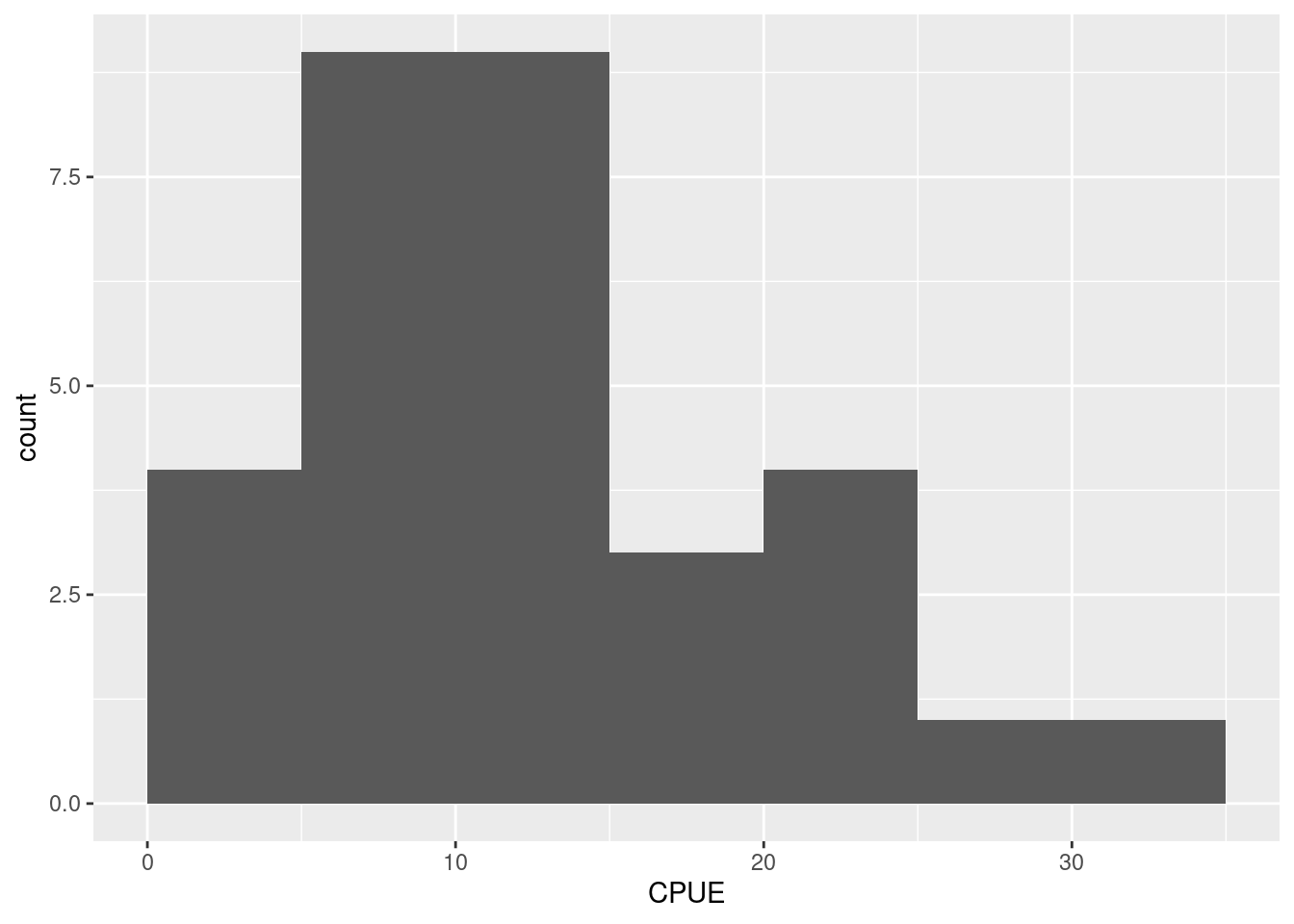
A formatação do histograma acima pode ser melhorada de diversas formas, por exemplo:
ggplot(res, aes(x = CPUE, label = ..count..)) +
geom_histogram(breaks = cl_cpue,
fill = 'darkblue', color = 'white') +
labs(x = 'Captura em kg', y = 'Frequência') +
geom_text(stat = "bin", size = 6, vjust = 1.5, color = 'white',
breaks = cl_cpue) +
theme_classic()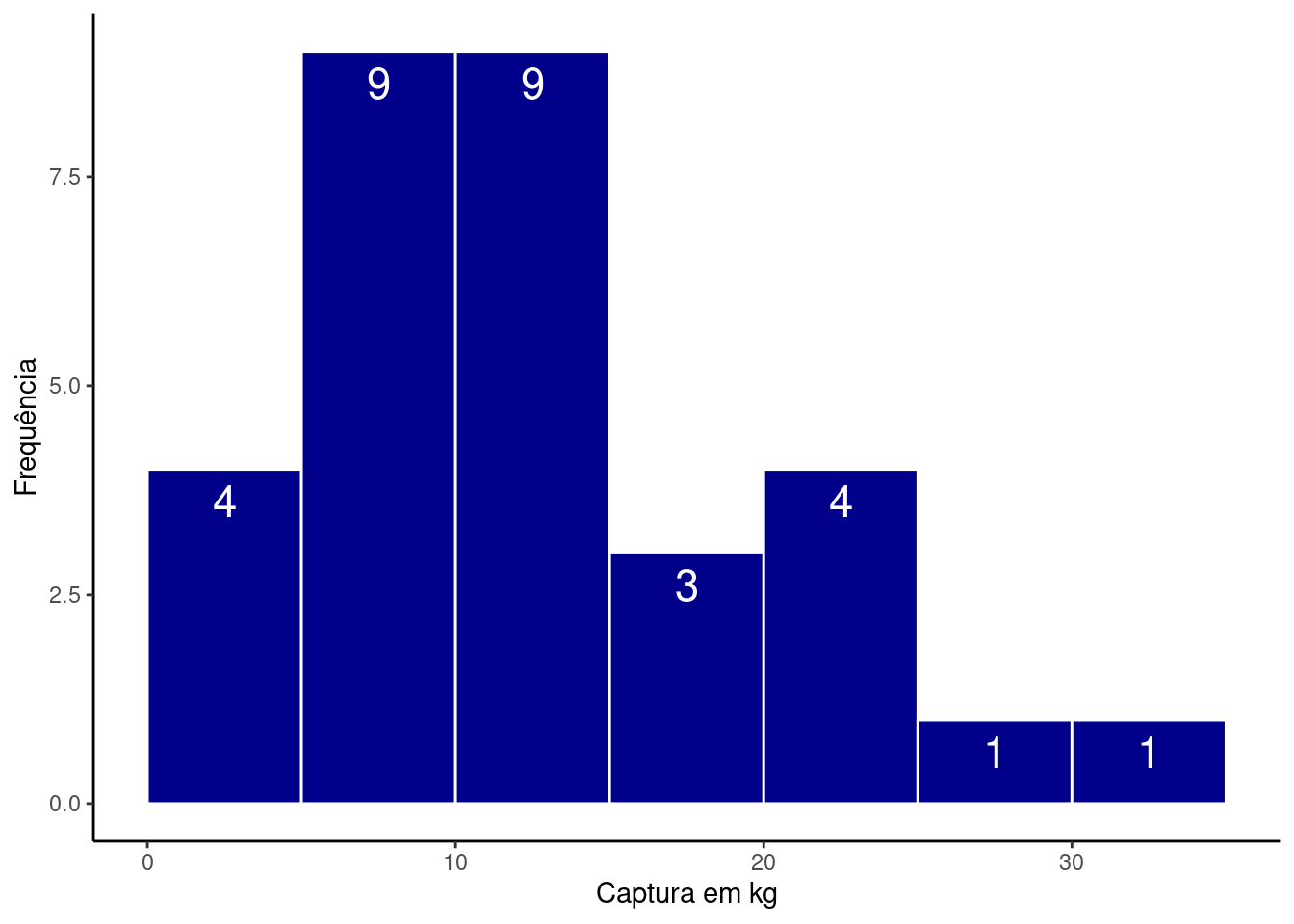
Modificamos a cor do preenchimento (
fill = 'darkblue'), e identificamos as barras individualmente traçando uma linha branca entre elas (color = 'white');Re-escrevemos o rótulo dos eixos \(x\) e \(y\) (
labs());identificamos as frequências em cada barra individualmente com o argumento
label = ..count..e a funçãogeom_text. Experimente alterar os argumentos dentro degeom_textpara entender cada um deles.modificamos o tema do gráfico para obter uma alteração geral na aparência da figura. Existem diversos outros temas possíveis que podem ser vistos aqui.
Um histograma com a frequência relativa pode ser obtido com:
ggplot(res, aes(x = CPUE,
y = (..count..)/sum(..count..),
label = round((..count..)/sum(..count..),2))) +
geom_histogram(breaks = cl_cpue,
fill = 'darkblue', color = 'white') +
labs(x = 'Captura em kg', y = 'Frequência relativa') +
geom_text(stat = "bin", size = 6, vjust = 1.5, color = 'white',
breaks = cl_cpue) +
theme_classic()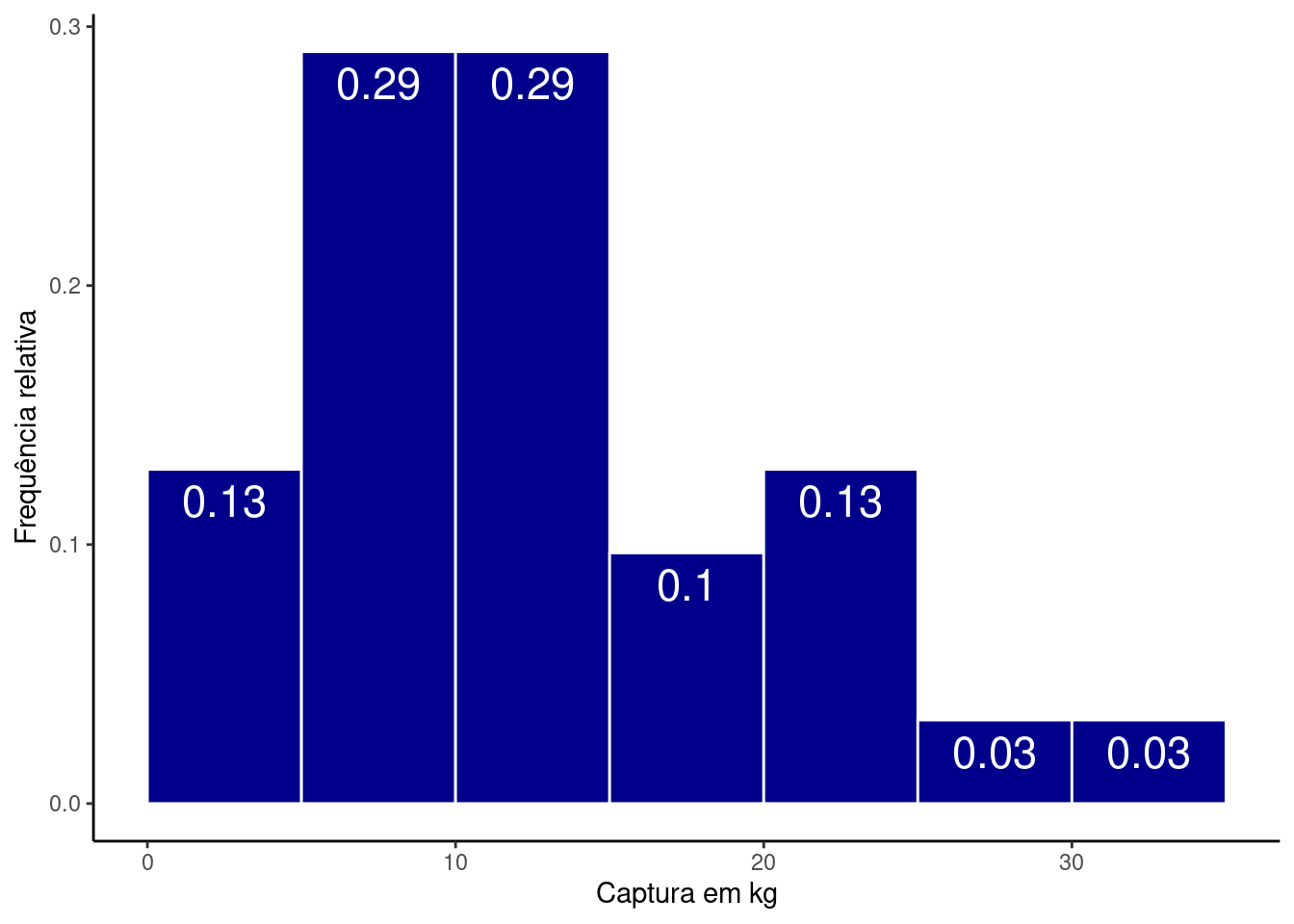
Aqui fizemos duas mudanças:
inserimos o argumento
y = (..count..)/sum(..count..)para dizer que as barras em \(y\) devem mostrar a contagem do número de observações em cada intervalo dividido pelo total e;modificamos o argumento
label = round((..count..)/sum(..count..),2)de modo que também mostre a frequência relativa. Neste argumento, entretanto, tivemos que utilizar uma função de arredondamentoround(__, 2)para dizer que os nomes abaixo das barras deveria ser mostrados somente com duas casas decimais.Finalmente, modificamos o nome do eixo \(y\) para
y = 'Frequência relativa'.
4.2.1 Representando frequências acumuladas
A única modificação neste caso será a identificarmos o eixo \(y\) por sua contagem acumulada: y=cumsum(..count..).
ggplot(res, aes(x = CPUE,
y = cumsum(..count..),
label = round(cumsum(..count..),2))) +
geom_histogram(breaks = cl_cpue,
fill = 'darkblue', color = 'white') +
labs(x = 'Captura em kg', y = 'Frequência acumulada') +
geom_text(stat = "bin", size = 6, vjust = 1.5, color = 'white',
breaks = cl_cpue) +
theme_classic()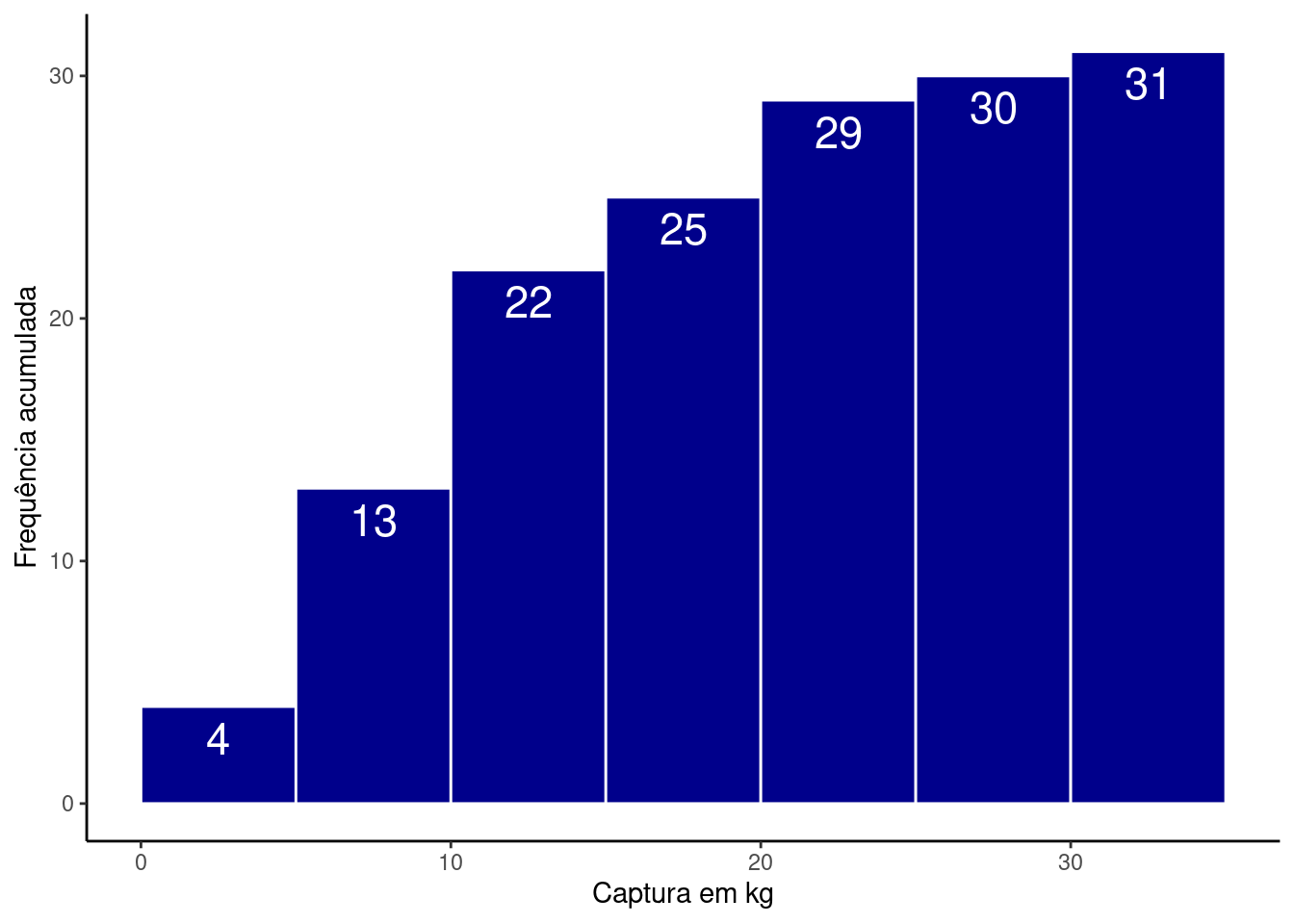
Para fazer o mesmo mostrando as frequências relativas fazemos:
ggplot(res, aes(x = CPUE,
y = cumsum(..count../sum(..count..)),
label = round(cumsum(..count../sum(..count..)),2))) +
geom_histogram(breaks = cl_cpue,
fill = 'darkblue', color = 'white') +
labs(x = 'Captura em kg', y = 'Frequência acumulada relativa') +
geom_text(stat = "bin", size = 6, vjust = 1.5, color = 'white',
breaks = cl_cpue) +
theme_classic()