Capítulo 19 Modelos lineares
Até agora estávamos nos referindo à nossa variável de interesse principal como variável \(X\). Nesta seção (Capítulos 19 a 25) iremos nos referir a uma variável resposta (ou variável dependente, \(Y\)), que será nossa variável de interesse principal e que será descrita como função de uma ou mais variáveis preditoras (ou variáveis independentes, \(X\)). Abordaremos novamente os conceitos de partição da soma dos quadrados, covariância e coeficiente de determinação no contexto do teste de hipóteses e ajuste de modelos. Neste sentido, esta seção tem relação direta com o que foi apresentado nos capítulos 10 e 11 e é interessante revê-los antes de continuar.
Modelos lineares compõem os modelos estatísticos clássicos para descrevermos o comportamento de uma variável resposta \(Y\) como função de uma ou mais variáveis preditoras \(X\)´s quando esta relação é linear. O formato básico de um modelo linear é:
\[Y = \beta_0 + \beta_1X + \epsilon\]
em que \(\beta_0\) e \(\beta_1\) são os parâmetros do modelo e \(\epsilon\) é denominado de resíduo do modelo. Nos modelos que veremos nesta seção, o resíduo tem distribuição normal com média \(0\) e variância constante \(\sigma^2\), ou seja:
\[\epsilon \sim \mathcal{N}(0, \sigma^2)\]
A parte inicial do modelo (\(\beta_0 + \beta_1X\)) forma a parte sistemática do modelo, enquanto \(\epsilon\) descreve a parte estocástica.
Quando existe mais de uma variável preditora, o modelo pode ser descrito como:
\[Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_pX_p + \epsilon\]
em que temos portanto \(p\) variáveis preditoras envolvidas.
\(Y\) consiste de uma variável contínua, enquanto as variáveis \(X\) em um modelo linear podem ser todas quantitativas (contínuas ou discretas), todas qualitativas (categóricas ou ordinais) ou conter uma combinação destes tipos. Os modelos que veremos nos capítulos desta seção são casos particulares de modelos lineares que variam em função do número de variáveis preditoras envolvidas e da natureza destas variáveis (quantitativas ou qualitativas). Deste modo temos por exemplo:
| Número de variáveis preditoras (\(X\)) | Quantitativa | Qualitativa | Modelo |
|---|---|---|---|
| Uma | X | ANOVA | |
| Uma | X | Regressão linear simples | |
| Duas ou mais | X | Regressão linear múltipla | |
| Duas ou mais | X | ANOVA fatorial | |
| Duas ou mais | X | X | ANCOVA |
19.1 Simulando um modelo linear no R
Vamos simular dois tipos de modelos lineares (o modelo de Regressão Linear e o modelo de Análise de Variância - ANOVA) utilizando uma notação comum. Nos capítulos seguintes cada um destes modelos será tratado de forma particular.
19.1.1 O Modelo de Regressão
Envolve uma única variável preditora contínua e três parâmetros desconhecidos, \(\beta_0\) e \(\beta_1\) e \(\sigma^2\).
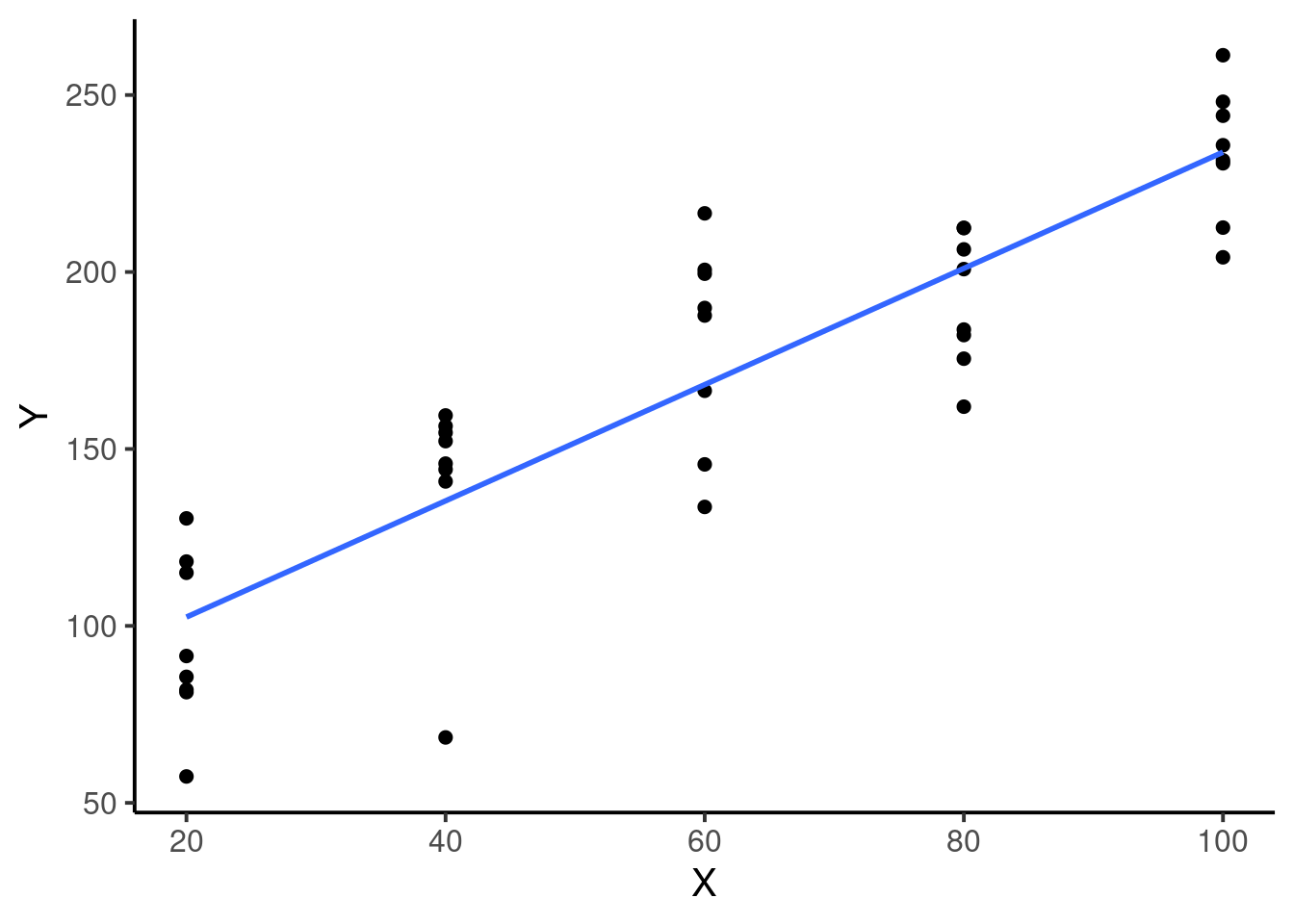
Neste modelo, os pontos mostram o resultado do modelo estatístico e a linha descreve a parte sistemática. O parâmetro \(\beta_0\) descreve a posição média em \(Y\) para um valor de \(X = 0\) e \(\beta_1\) a taxa de incremento médio em \(Y\) para a deferença de uma unidade em \(X\). O parâmetro \(\sigma\) se refere ao desvio padrão do resíduo e define o grau de espalhamento dos pontos ao redor da reta média. Experimente diminuir e aumentar o valor de \(\sigma\) e verifique o que ocorre com a dispersão dos pontos.
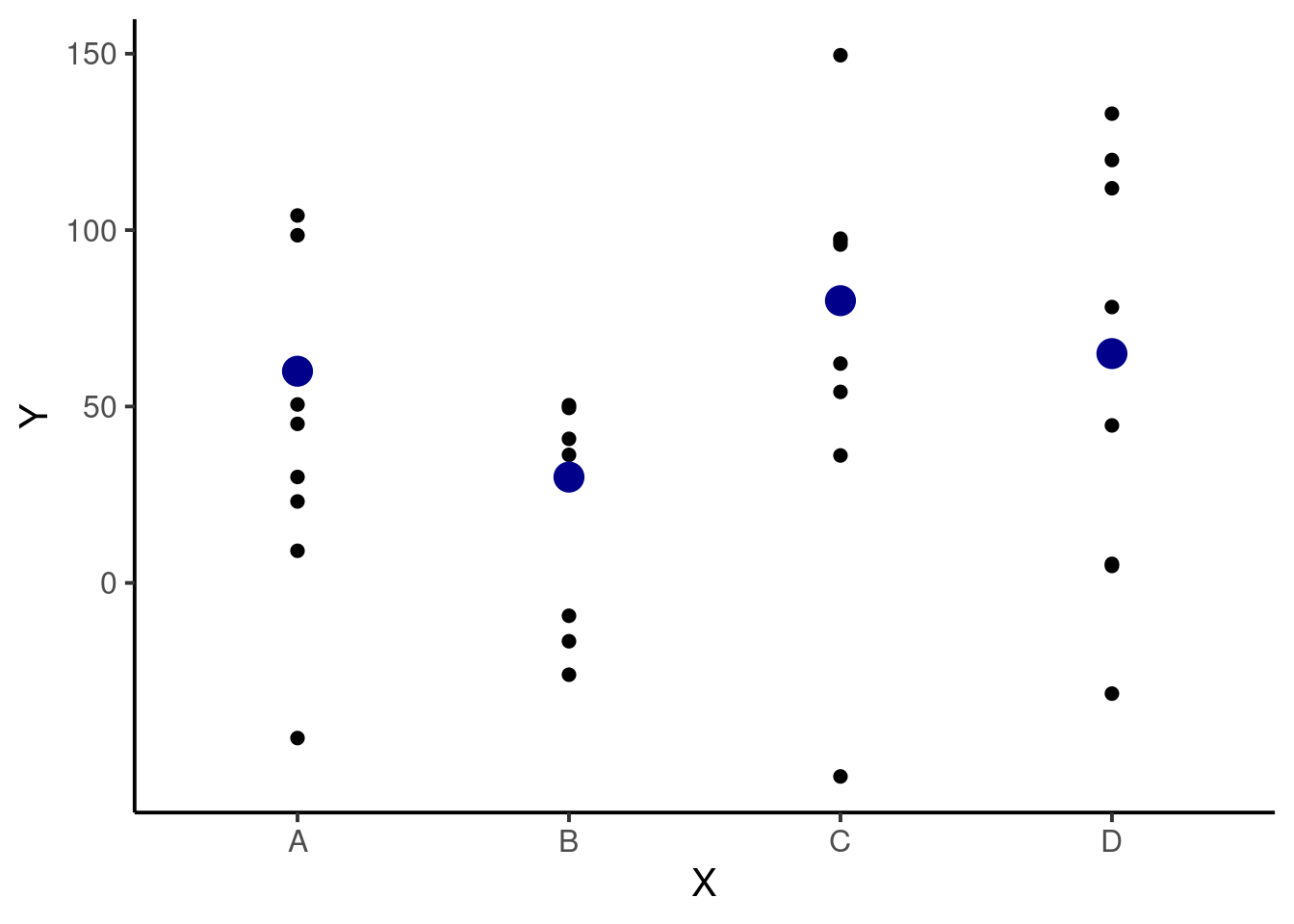
19.1.2 Modelo de ANOVA
Neste caso a variável preditora \(X\) é categórica. Vamos criar uma variável \(X\) com 4 níveis (A, B, C e D) em um experimento com \(8\) repetições (réplicas) por nível, totalizando \(n = 8 \times 4 = 40\) observações. Quando modelos de ANOVA são representados como modelos lineares, a variável categórica deve ser transformada em uma (no caso de dois níveis) ou mais variáveis indicadoras (ou variáveis dummy). Esta transformação é consiste basicamente em criar variáveis do tipo \(0/1\) que indiquem todas as combinações de níveis do experimento. Para entender melhor, acesse o link: Dummy variable (statistic).
Os comandos neste caso são mais complexos que na regressão simples, mas seguem a mesma lógica de criarmos as variáveis preditoras e somá-las ao ressíduo do modelo.
Nestes comandos criamos uma variável preditora \(X\) com \(4\) níveis, as transformamos em uma variável indicadora e criamos os valores de \(\mu_A\), \(\mu_B\), \(\mu_C\) e \(\mu_D\), de modo que:
\(\mu = \beta_0 = 50\): média geral
\(\mu_A = \beta_0 + \beta_1 = 50 + 10\): média do tratamento A
\(\mu_B = \beta_0 + \beta_2 = 50 + -20\): média do tratamento B
\(\mu_C = \beta_0 + \beta_3 = 50 + 30\): média do tratamento C
\(\mu_D = \beta_0 + \beta_4 = 50 + 15\): média do tratamento D
As notações \(\mu_{A \cdots D}\) são respectivamente as médias populacionais dos tratamentos, conforme iremos definir no capítulo sobre Análise de Variância (ANOVA - capítulo 20). Deste modo, o gráfico de dispersão resultante deste modelo contém variáveis preditoras categóricas em que os pontos estão espalhados ao redor da media \(\mu\) (em azul) do respectivo tratamento de acordo com a magnitude de \(\sigma\) .