Capítulo 27 Combinando as probabilidades de eventos
No capítulo anterior, falamos sobre espaço amostral e a definição de probabilidade. Aqui vamos combinar eventos de um espaço amostral e calcular as probabilidades de eventos complexos.
27.1 Eventos complexos
Vamos assumir que o sucesso na capacidade de forrageamento de um organismo depende de uma série de fatores relacionados à densidade da presa, à capacidade sensorial do predador, de sua eficiência em capturar/manipular o alimento, entre outros fatores. Para exemplo do Acará (Capítulo 26), o sucesso depende de virar a estrutura certa, a que tenha maior número de presas disponíveis.
Para simplificar consideremos a seguintes condições. Existem dois tipos de estruturas principais sobre as quais o acará forrageia: folhas e galhos. Folhas podem ter entre 0 e 6 itens enquanto galhos podem ter entre 0 e 4 itens. Uma vez que o predador vira uma estrutura ele se alimenta de todos os itens presentes. Certamente, esta é uma situação altamente hipotética, mas que facilita nossa discussão. A pergunta aqui é: ao virar uma estrutura, de quantos itens um predador poderá se alimentar?
Vamos as possibilidades. Denominemos por \(F\) ou \(G\) o encontro de uma folha ou galho respectivamente e de \(0\) a \(n\), o número de itens encontrados. O espaço amostral do experimento virar uma estrutura e contar o número de itens consiste de:
\(\Omega = \{(F0), (F1), (F2), (F3), (F4), (F5), (F6), (G0), (G1), (G2), (G3), (G4)\}\)
Neste experimento temos 12 eventos simples e mutuamente exclusivos
Considere agora o evento \(A\) “virar uma folha”. que pode ocorrer pela observação de F0 ou F1 ou F2 ou F3 ou F4 ou F5 ou F6.
\(A = \{(F0), (F1), (F2), (F3), (F4), (F5), (F6)\}\)
27.1.1 Representação de eventos: diagrama de Venn
Uma forma de visualizar o espaço amostral e eventos deste espaço é pela construção de diagramas de Venn. Para isto, vamos considerar também o evento \(B\) “encontrar mais de 3 itens” que consiste de:
\(B = \{(F3), (F4), (F5), (F6), (G3), (G4)\}\)
Observando os eventos \(A\) e \(B\) em um Diagrama de Venn temos:
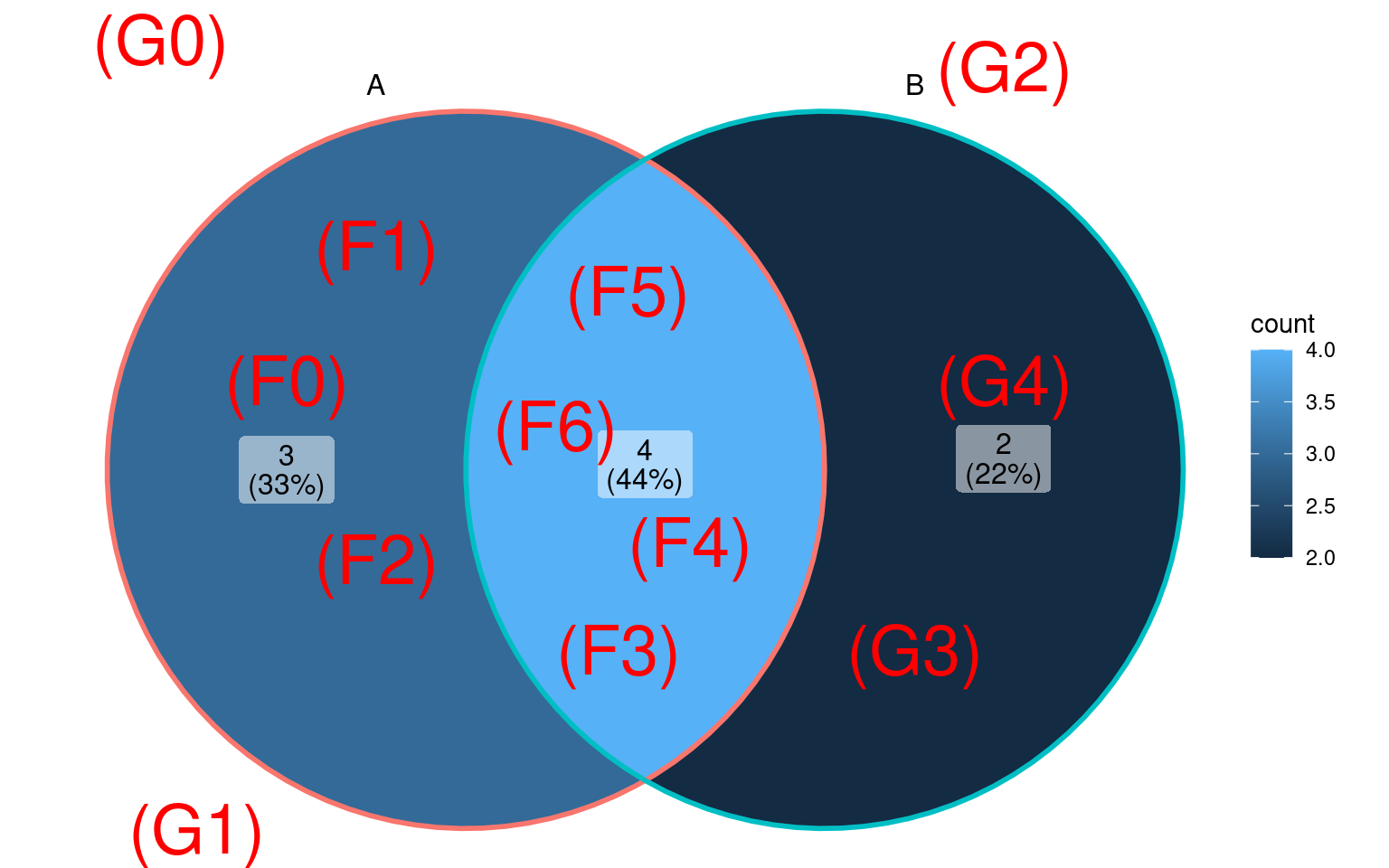
Cada um destes eventos é denominado de evento complexo, pois pode ser obtido pela combinação de eventos simples. O evento \(B\) por exemplo, pode ocorrer quando é encontrado uma folha OU um galho com mais de 3 itens, enquanto o evento \(A\) ocorre quando é encontrada uma folha com \(0\) OU \(1\) OU \(2\) OU \(3\) OU \(4\) OU \(5\) OU \(6\) itens.
Estes eventos complexos foram obtidos por meio da união de eventos simples. A declaração OU significa que qualquer uma destas observações é suficiente para dizer que o evento ocorreu. Ou seja, \(A\) pode ocorrer por 7 formas e \(B\) por 6 formas distintas.
Note que as observações \((G0)\), \((G1)\) e \((G2)\) não pertencem aos eventos \(A\) nem \(B\), ainda que estejam no espaço amostral \(\Omega\) de possibilidades.
Considere agora o evento \(C\) virar uma folha mais de 3 itens. \(C\) pode ocorrer a partir de F3 ou F4 ou F5 ou F6. No diagrama de Venn, vemos que estas opções consistem da intersecção de \(A\) e \(B\). Ou seja, as observações que satisfazem \(C\) em ambos os eventos anteriores. Você verá em livros de probabilidade que o termo de união é representado pelo símbolo \(\cup\), enquanto o termo de intersecção é representado por \(\cap\).
Assim, temos que \(C\) pode ser excrito como \(A \cap B\).
27.1.2 Probabilidade de eventos simples
Considerando o experimento virar uma estrutura e contar o número de itens, qual seria a probabilidade da ocorrência de cada observação? Para isto, devemos inicialmente lembrar que:
O espaço amostral consiste de \(N = 12\) observações e;
Definir um modelo de probabilidade para cada uma destas observações.
Neste tópico vamos assumir um modelo de probabilidade uniforme em que cada observação tem a mesma probabilidade. Iremos assumir este modelo somente para iniciar a discussão. Outros tipos de modelos com suas respectivas aplicações serão considerados nos capítulo 30. Portanto, assumindo este modelo uniforme, cada observação individual tem probabilidade \(\frac{1}{N}\).
Diante disto, a probabilidade da ocorrência do evento \(A\) será o número de ocorrências favoráveis a \(A\) dividido pelo número de resultados do espaço amostral. Como \(A\) consiste de 7 observações, então:
\[P(A) = \frac{7}{12} = 0.58\]
Naturalmente, a probabilidade de \(A\) não ocorrer será:
\[P(\overline{A}) = 1 - \frac{7}{12} = 1 - 0.58 = 0.42\] Obs. O símbolo \(\overline{A}\) significa todas as observações que não pertencem a \(A\).
Considere também a probabilidade do evento \(B\):
\[P(B) = \frac{6}{12} = 0.5\] e do evento \(C = A \cap B\)
\[P(C) = P(A \cap B) = \frac{4}{12} = 0.33\]
27.1.3 Probabilidade da união de eventos
Vamos ao evento \(A \cup B\) que consiste de todas a observações que estejam em \(A\) ou \(B\):
\(A \cup B = \{(F0),(F1),(F2),(F3),(F4),(F5),(F6),(G3),(G4) \}\)
Temos então que esta união consiste de 9, de modo que:
\[P(A \cup B) = \frac{9}{12} = 0.75\]
Veja que \(P(A \cup B)\) pode ser obtido por:
\(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
27.1.4 Representação de eventos: diagrama de árvore
Considere agora o experimento “virar duas estruturas e verificar o tipo de estrutura”. O espaço amostral deste experimento consiste de 4 observações:
\(\Omega = \{(galho, galho), (galho, folha), (folha, galho), (folha, folha)\}\)
E pode ser representado visualmente por um diagrama de árvore.
REFAZER DIAGRAMA DE ÁRVORE. Função ‘bayes_probability_tree()’ desatualizada
O diagrama de árvore é útil quando desejamos representar os resultados possíveis de um experimento que consiste de múltiplas etapas consecutivas, possivelmente composto por mais de uma caminho possível. Utilizaremos novamente este tipo de diagrama para falarmos em probabilidade condicional (Capítulo 28) e do Teorema de Bayes (Capítulo 29).