Capítulo 29 Teorema de Bayes: atualizando o conhecimento
29.1 Teorema de Bayes
O teorema de Bayes decorre de nossa definição de probabilidade condicional em que:
\[P(B|A) = \frac{P(A \cap B)}{P(A)}\]
o que implica em:
\[P(A \cap B) = P(A) \times P(B|A)\]
Das expressões acima, poderíamos escrever também que:
\[P(A|B) = \frac{P(B \cap A)}{P(B)}\] e
\[P(B \cap A) = P(B) \times P(A|B)\]
Uma que \(P(A \cap B) = P(B \cap A)\), temos que:
\[P(A) \times P(B|A) = P(B) \times P(A|B)\]
o que nos leva à expressão que define o Teorema de Bayes e nos fornece a probabilidade condicional de \(P(B|A)\) uma vez que conhecemos \(P(A|B)\).
\[P(B|A) = \frac{P(B) \times P(A|B)}{P(A)}\]
29.2 Teorema da probabilidade total
Veja novamente a esquema concentual de um diagrama de árvore:
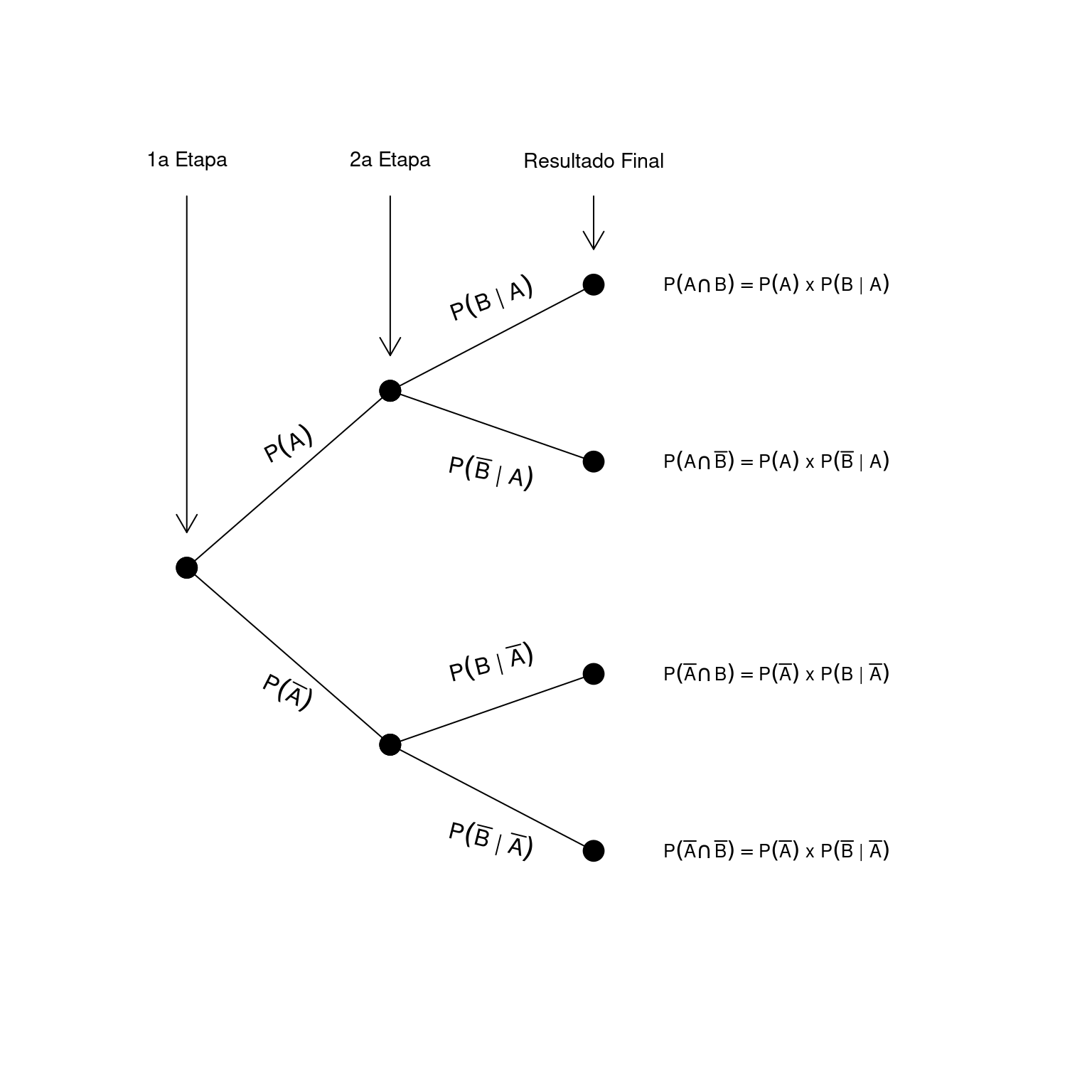
Podemos perceber que dois caminhos nos levam à ocorrência de \(A\). Um caminho em que \(B\) também ocorre - com probabilidade \(P(A \cap B)\) - ou um caminho em que \(B\) não ocorre - com probabilidade \(P(A \cap \overline{B})\). Uma vez que estas rotas são mutuamente exclusivas, \(P(A)\) pode ser calculado por:
\[P(A) = P(A \cap B) + P(A \cap \overline{B})\]
que podemos re-escrever como:
\[P(A) = P(B) \times P(A|B) + P(\overline{B}) \times P(A|\overline{B})\]
Esta última expressão é conhecida como Teorema da probabilidade total. Ao utilizá-la, o Teorema de Bayes pode ser re-escrito como:
\[P(B|A) = \frac{P(B) \times P(A|B)}{P(B) \times P(A|B) + P(\overline{B}) \times P(A|\overline{B})}\]
29.3 O problema da detecção de espécies
Suponha um estudo sobre a distribuição de uma espécie de peixe em uma área de restinga da Mata Atlântica. A espécie ocorre em poças formadas pela água da chuva e está presente em 5% das poças na região. Isto denota uma espécie rara, pois ao investigarmos uma poça em particular, sua probabilidade de ocorrência será de \(P(O) = 0,05\).
A detecção desta espécie é feita pela captura e identificação taxonômica. Dado que esteja presente em uma poça, sua probabilidade de ser capturada é de \(0,99\). Consequentemente, existe uma probabilidade de \(0,01\) de que, mesmo estando presente, a espécie não seja capturada, o que é conhecido como falso negativo. Um falso negativo pode acontecer por exemplo se os indivíduos permanecem escondidos sob o substrato e não são capturados.
Sabe-se também que existe na região uma espécie muito similar e, por vezes, ocorre um erro de identificação. Desta forma, mesmo nas poças em que a espécie não está presente, existe uma possibilidade de que seja registrada erroneamente, o que pode ocorrer com probabilidade de \(0,10\). Chamamos esta possibilidade de falso positivo. O problema da não-detecção ou da falsa-detecção, longe de ser somente um exemplo, é comum em levantamentos de fauna e flora ainda que raramente seja considerado.
As probabilidades descritas neste problema podem ser organizadas em um diagrama de árvore.
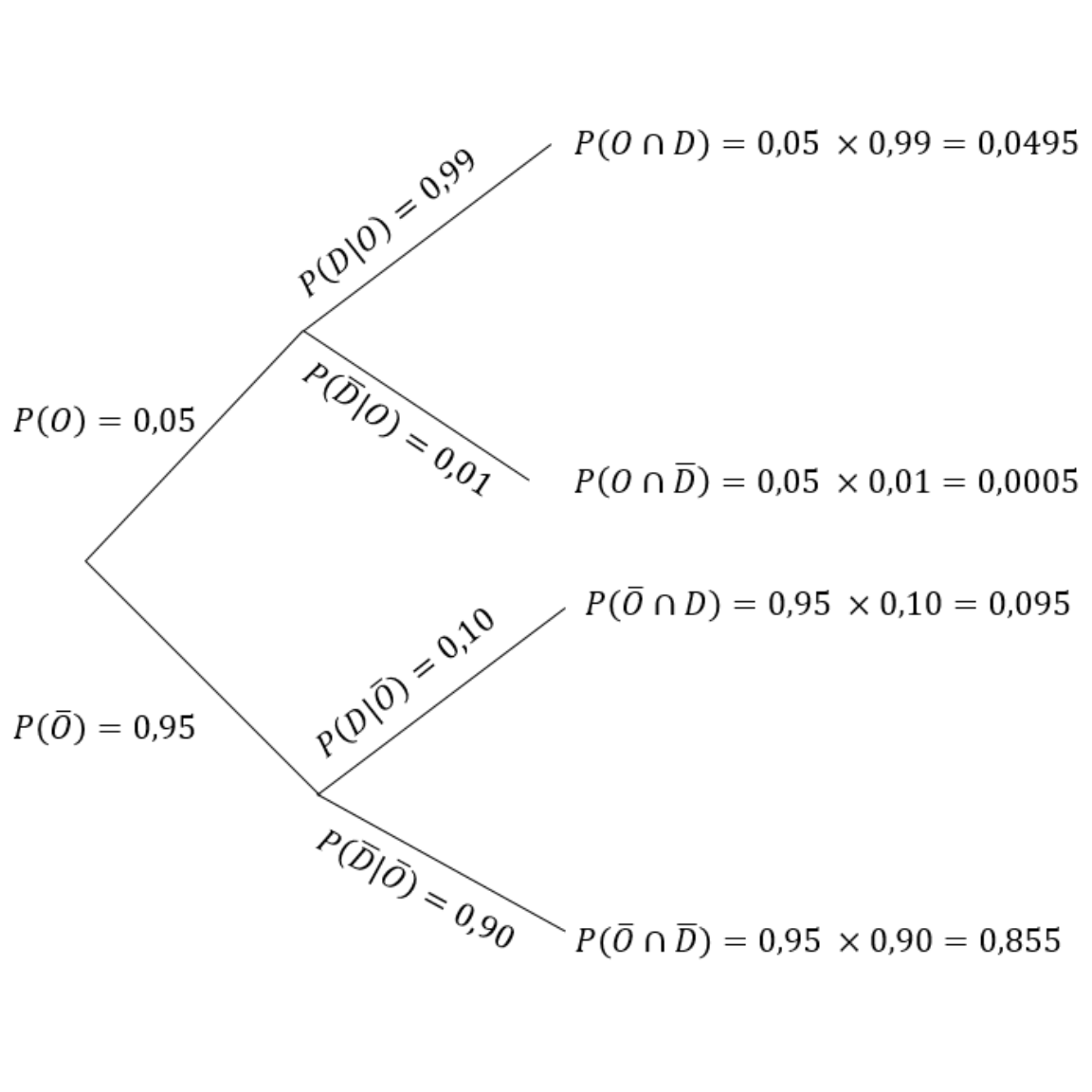
Figure 29.1: Diagrama de árvore representando as probabilidades de ocorrência P(O) e detecção P(D) de uma espécie.
No diagrama, cada bifurcação representa as possíveis saídas de um estágio do experimento. Por exemplo, em uma determinada poça a espécie está ou não está presente, com probabilidades \(0,05\) e \(0,95\) respectivamente. O segundo estágio do experimento consiste na tentativa de detecção da espécie. Neste caso, as possibilidades são as seguintes:
Dado que a espécie esteja presente, os resultados possíveis são: i) ocorre a detecção com probabilidade \(0,99\) ou ii) não ocorre a detecção com probabilidade \(0,01\).
Dado que a espécie não esteja presente, os resultados possíveis são: i) a ocorrência é registrada erroneamente com probabilidade \(0,10\) ou ii) a ocorrência não é registrada com probabilidade \(0,90\).
Diante deste cenário, temos como possíveis resultados:
A espécie Ocorre e é Detectada com probabilidade \(P(O \cap D) = 0,0495\)
A espécie Ocorre porém permanece Não-Detectada com probabilidade \(P(O \cap \bar{D}) = 0,0005\)
A espécie Não Ocorre e é Detectada erroneamente com probabilidade \(P(\bar{O} \cap D) = 0,095\)
A espécie Não Ocorre e permanece Não-Detectada com probabilidade \(P(\bar{O} \cap\overline{D}) = 0,855\)
De acordo com o Teorema da probabilidade total, \(P(D)\) pode ser calculada:
\[P(D) = P(O \cap D) + P(\bar{O} \cap D) = 0,0495 + 0,095 = 0,1445\]
pois o registro de detecção pode ocorrer quando a espécie está ou não está presente na poça.
29.3.1 Razão de verossimilhança, inferência bayesiana e teste de hipóteses
Um questão relevante neste problema é:
Ao recebermos a notícia de uma possível detecção, deveríamos ficar completamente convencidos sobre a ocorrência desta espécie em uma determinada poça?
Esta questão é importante pois nos permite tomar uma decisão sobre um fenômeno que não conhemos (a ocorrência da espécie na poça), com base na informação sobre uma possível detecção. A tomar esta decisão, entramos no campo da inferência estatística. Nos capítulos 16 e 17 discutimos a ideia da inferência estatística clássica, onde introduzomos conceitos como Erro do Tipo I, do Tipo II e poder do teste. Ńesta seção iremos introduzir outras duas abordagens, a inferência por verossimilhança e a inferência bayesiana. Ambas serão tratadas mais detalhadamente nos capítulos 34 a 36.
Verossimilhança: uma medida indireta para \(P(O|D)\)
Veja que, ao existir a possibilidade de um falso negativo, a ocorrência da espécie deve ser tomada como uma hipótese a ser confirmada. Caso \(P(D|O)\) seja elevado, deveríamos estar bastante confiantes sobre a ocorrência da espécie, pois a probabilidade de detectá-la seria alta quando ela, de fato, ocorre. Por outro lado, caso \(P(D|\overline{O})\) seja elevado, deveríamos estar mais confiantes da não-ocorrência da espécie, pois sua probabilidade de detecção seria alta mesmo nas situações em que não esteja presente (falso positivo).
Em inferência estatística, \(P(D|O)\) pode ser tomada como uma medida de verossimilhança para a hipótese de ocorrência da espécie condicional ao evento de detecção. Como discutimos ao longo deste capítulo, \(P(D|O)\) não é igual a \(P(O|D)\), porém as duas medidas são positivamente relacionadas, uma vez que \(P(O|D)\) é uma função positiva crescente de \(P(D|O)\).
Estritamente falando, a probabilidade condicional \(P(D|O)\) não é realmente sinônimo de verossimilhança. A função de verossimilhança seria expressa por \(\mathcal{L}(O|D)\) (note a inversão nas posições \(O\) e \(D\)). Dizemos portanto que \(P(D|O) \propto \mathcal{L}(O|D)\) (é proporcional à) e isto ficará mais claro nos capítulos 30 a 36. Por hora, vamos tratar os dois conceitos como análogos.
Assim como \(P(D|O)\) pode ser utilizada para medir o grau de confiabilidade na ocorrência da espécie, \(P(D|\overline{O})\) pode ser utilizada para medir o grau de confiabilidade da não-ocorrência. Têm-se então duas hipóteses a serem contrastadas:
Hipótese 1: a espécie ocorre e foi detectada;
Hipótese 2: a espécie não ocorre porém foi detectada.
As medidas que nos permitem contrastar as hipóteses 1 e 2 são \(P(D|O)\) e \(P(D|\overline{O})\). Utilizando-as, podemos calcular o que denominamos de razão de verossimilhanças (\(RV\)), tomando a razão entre a maior e a menor medida, de modo que:
\[RV = \frac{P(D|O)}{P(D|\overline{O})} = \frac{0,99}{0,10} = 9,9\]
Interpretamos o resultado acima dizendo que a hipótese da ocorrência (hipótese 1) é cerca de 10 vezes mais verossímil que a hipótese da não-ocorrência. \(RV\) nos fornece portanto, uma medida indireta sobre a expectativa de ocorrência da espécie, uma vez registrada sua detecção. Neste caso, o resultado foi favorável à Hipótese 1.
Inferência bayesiana: o conhecimento a priori é importante?
A ideia da verossimilhança parte unicamente do resultado obtido no experimento e de nosso pressoposto sobre a probabilidade do evento \(D\) condicional aos eventos \(O\) e \(\overline{O}\). Não utilizamos no entanto, a informação sobre \(P(O)\) que nos é fornecida no início do problema.
Ao utilizarmos \(P(O)\), entramos no campo da inferência bayesiana. Note que \(P(O)\) foi uma informação fornecida no início do experimento, antes da informação sobre uma possível detecção. Em inferência bayesiana, esta medida é conhecida como a probabilidade a priori para a ocorrência da espécie. Esta probabilidade foi obtida antes do evento de detecção, e geralmente parte de um conhecimento prévio que pode ser obtido a partir da literatura, de experimentos piloto ou do conhecimento empírico de especialistas.
Ao obtermos uma informação sobre uma possível detecção, devemos atualizar nossa hipótese sobre a ocorrência, que agora será condicional à observação do evento \(D\). Deste modo, em inferência bayesiana temos como informações de entrada:
As probabilidades a priori \(P(O)\) e \(P(\overline{O})\); e,
A informação sobre \(P(D|O)\) e \(P(D|\overline{O})\)
que utilizamos diretamente para calcular \(P(O|D)\) e \(P(\overline{O}|D)\).
Isto é feito utilizando o Teorema de Bayes que, neste exemplo, pode ser re-escrito como:
\[P(O|D) = \frac{P(O) \times P(D|O)}{P(O) \times P(D|O) + P(\overline{O}) \times P(D|\overline{O})}\]
Fazendo cálculos com as informações fornecidas no início do problema, a probabilidade de ocorrência dado o evento de detecção será:
\[P(O|D) = \frac{0,02 \times 0,99}{0,02 \times 0,99 + 0,98 \times 0,10} \approx 0.17\]
Enquanto a probabilidade de não-ocorrência será de:
\[P(\bar{O}|D) = \frac{0,98 \times 0,10}{0,02 \times 0,99 + 0,98 \times 0,10} \approx 0.83\]
Estes resultados nos dizem que, mesmo ao ser informados sobre uma possível detecção, a chance de não-ocorrência da espécie em uma determinada poça ainda é cerca de 5 vezes maior que a chance de ocorrência, o que é favorável à Hipótese 2.
Entendendo as diferênças entre as duas abordagens
As conclusões das duas abordagens foram distintas. Desta forma, é necessário entendermos melhor em quais causas destas diferenças, ou seja, em quais informações cada abordagem está baseada.
Enquanto a abordagem por verossimilhança utiliza \(P(D|O)\) para nos auxiliar indiretamente no julgamento das hipóteses 1 e 2, a inferência bayesiana utiliza o Teorema de Bayes para calcular diretamente \(P(O|D)\). Nesta última, \(P(O|D)\) pode ser entendida como uma média ponderada de \(P(D|O)\), em que os fatores de ponderação são as probabilidades a priori \(P(O)\) e \(P(\overline{O})\).
Temos portanto, que a ideia da probabilidade a priori é central e inferência bayesiana, porém irrelevante na inferência por verossimilhança. Vejam por exemplo o que ocorreria se as probabilidades a priori fossem \(P(O) = P(\overline{O}) = 0,5\).
Neste caso:
\[P(O|D) = \frac{0,5 \times 0,99}{0,5 \times 0,99 + 0,5 \times 0,10} = \frac{0,5}{0,5} \times \frac{0,99}{0,99 + 0,10} = \frac{0,99}{0,99 + 0,10} \approx 0,91 \]
e
\[P(\overline{O}|D) = \frac{0,5 \times 0,10}{0,5 \times 0,99 + 0,5 \times 0,10} = \frac{0,5}{0,5} \times \frac{0,10}{0,99 + 0,10} = \frac{0,10}{0,99 + 0,10} \approx 0,09 \]
Ao dividirmos \(P(O|D)\) por \(P(\overline{O}|D)\) terímos:
\[\frac{P(O|D)}{P(\overline{O}|D)} = \frac{0,91}{0,09} = 9,9\]
O que é exatamente igual à razão de verossimilhança \(RV\) obtida anteriormente.
Ao dizer que \(P(O) = P(\overline{O}) = 0,5\), estamos dizendo que, a priori do experimento, sabemos unicamente que um espécie tem changes iguais de estar ou não estar presente. Em inferência bayesiana esta informação é conhecida como priori não-informativa, pois dá pesos iguais a todas as possibilidades. Por outro lado, quando informamos em nosso exemplo que a espécie é muito rara, os fatores de ponderação (\(P(\overline{O}) = 0,95\) versus \(P(O) = 0,05\)) tornaram-se muito influentes no cálculo de \(P(O|D)\), independente do resultado de uma possível detecção da espécie.
Portanto, as duas abordagens serão equivalentes somente quando utilizamos uma priori não informativa. Isto equivale a dizer que, por não termos informações melhores, estamos dando chances iguais para os eventos \(O\) e \(\overline{O}\).