Capítulo 31 As variáveis são aleatórias, não imprevisíveis! - Modelos contínuos
No capítulo 30 exemplificamos uma série de modelos probabilísticos em que a variável aleatória tem uma natureza discreta. Aqui vamos exemplificar modelos contínuos. Uma variável aleatória contínua é representada por conjuntos numéricos não-contáveis, por exemplo a distância de deslocamento/dia de um organismo, o peso de um indivíduo, a temperatura da água, etc (Capítulo ??).
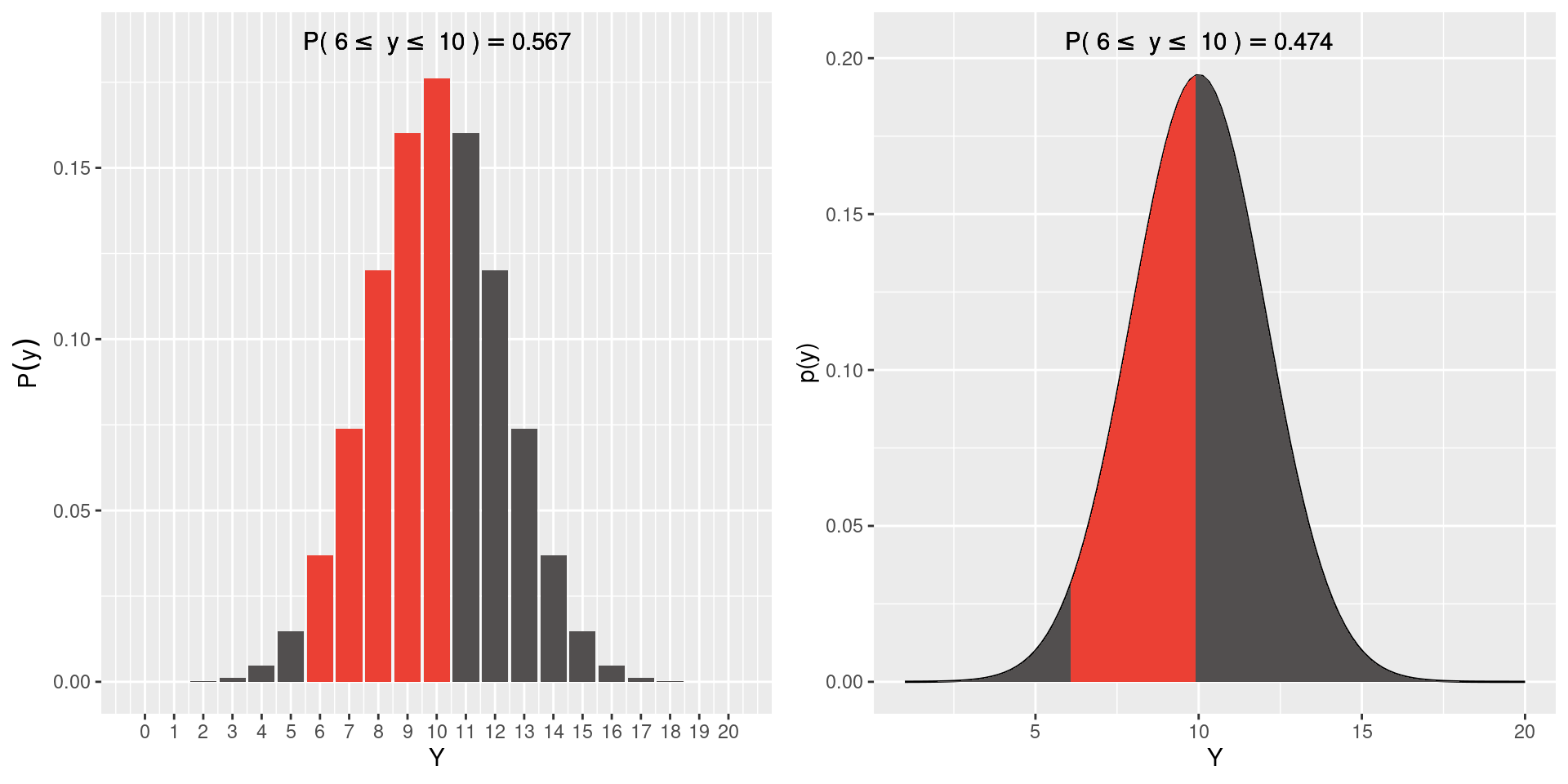
Ao tratar de modelos probabilísticos para variáveis aleatórias contínuas devemos fazer uma distinção do que foi apresentado anteriormente. Nos modelos discretos, é possível por exemplo falarmos na probabilidade de um experimento resultar em um valor particular de \(y\), ou seja, \(P(Y = y)\).
Neste caso:
\[P(-\infty \le Y \le +\infty) = \sum_{-\infty}^{+\infty} p(y) = 1\] Para variáveis contínuas podemos expressar somente a probabilidade de que um experimento resulte em um intervalo de valores entre \(a\) e \(b\), ou seja, \(P(a \le y \le b)\). Deste modo temos que:
\[P(-\infty \le Y \le +\infty) = \int_{-\infty}^{+\infty}p(y) dy = 1\]
Portanto, para as variáveis contínuas, o conceito de somatório dos valores individuais para \(y\) é substituído pelo conceito de integração em um intervalo definido e a probabilidade deste intervalo equivale à área sob a curva de probabilidade.
Esperança e variância em modelos contínuos
Vimos que o valor esperado para uma variável aleatória discreta é dado por:
\[E(Y) = \sum_i^n y_i \times p(y_i)\] Para uma variável aleatória contínua, podemos definir o valor esperado como:
\[E(Y) = \int_{-\infty}^{+\infty}y \times f(y) dy\]
Note que aqui, substituímos \(p(y_i)\) por \(f(y)\), uma vez que em um modelo contínuo, \(f(y)\) não nos dá a probabilidade da ocorrência de um determinado valor \(y_i\), mas é entendido como uma função de densidade.
A variância no modelo contínuo ainda é definida como:
\[VAR(Y) = E(Y^2) - (E(Y))^2\]
31.1 Alguns fenômenos têm distribuição normal
Suponha que ao amostrar indivíduos de uma espécie de Rhamdioglanis transfasciatus em um riacho, você tenha interesse em medir o comprimento da cada indivíduo. Se assumirmos um Modelo Normal para a variável aleatória comprimento, veremos que a maioria dos indivíduos terá tamanhos próximos à média \(\mu\) e poucos indivíduos serão muito grandes ou pequenos.
Uma variável aleatória com distribuição normal, tem sua função de densidade de probabilidade definida por:
\[f(y|\mu,\sigma) = \frac{1}{\sqrt(2\pi\sigma^2)}e^{-\frac{1}{2}(\frac{y-\mu}{\sigma})^2}\]
Em que os parâmetros da função são \(\mu\) e \(\sigma\) representam respectivamente a média e o desvio padrão de \(y\). Novamente nos referimos aos símbolos da média e desvio padrão conforme a notação utilizada para descrever a população estatística de um experimento (Capítulo ??). Na função de densidade estes parâmetros determiman a prosição central e o grau de achatamento da curva.
Após o término deste tópico é importante que você leia também o que foi apresentado no capítulo 14 sobre distribuição normal.
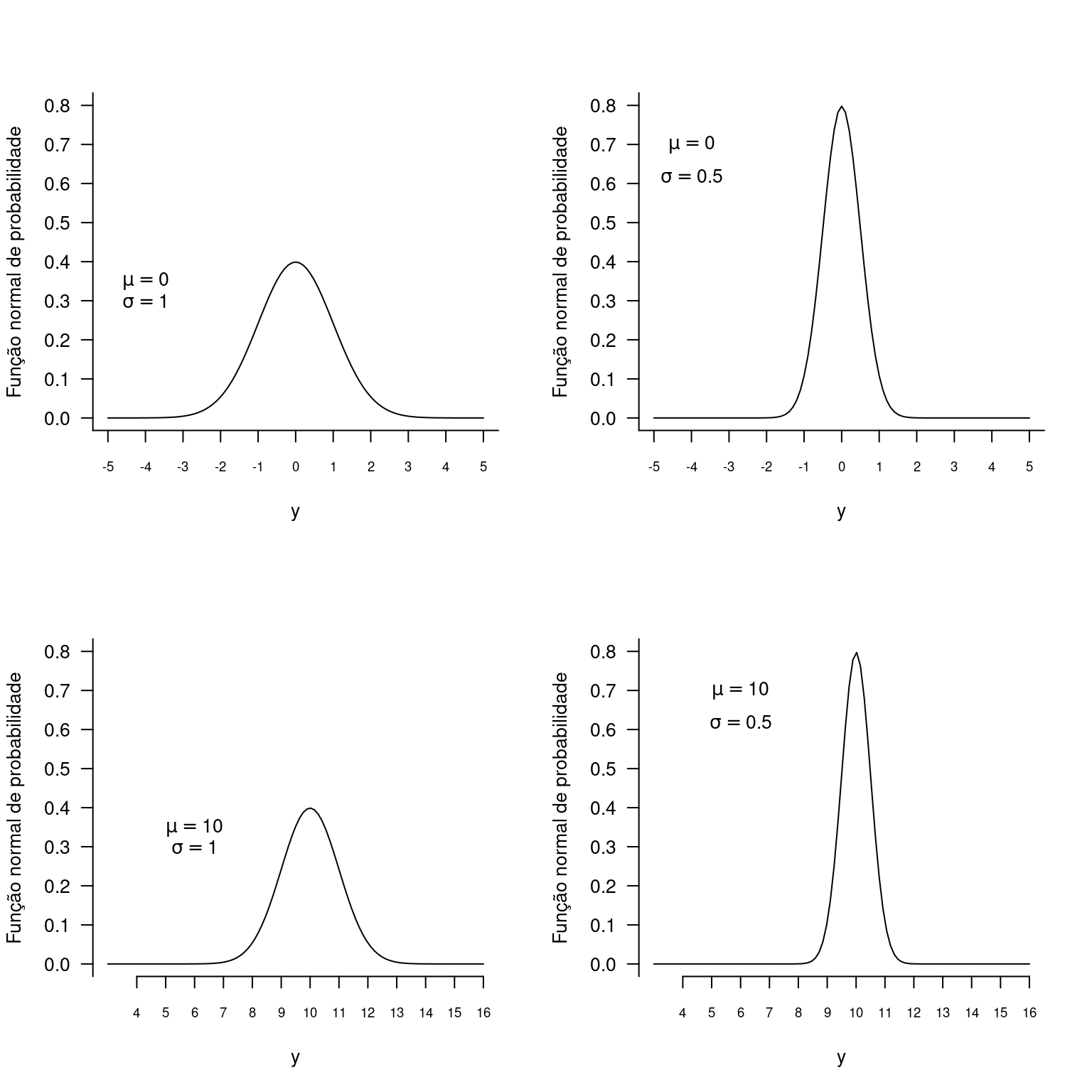
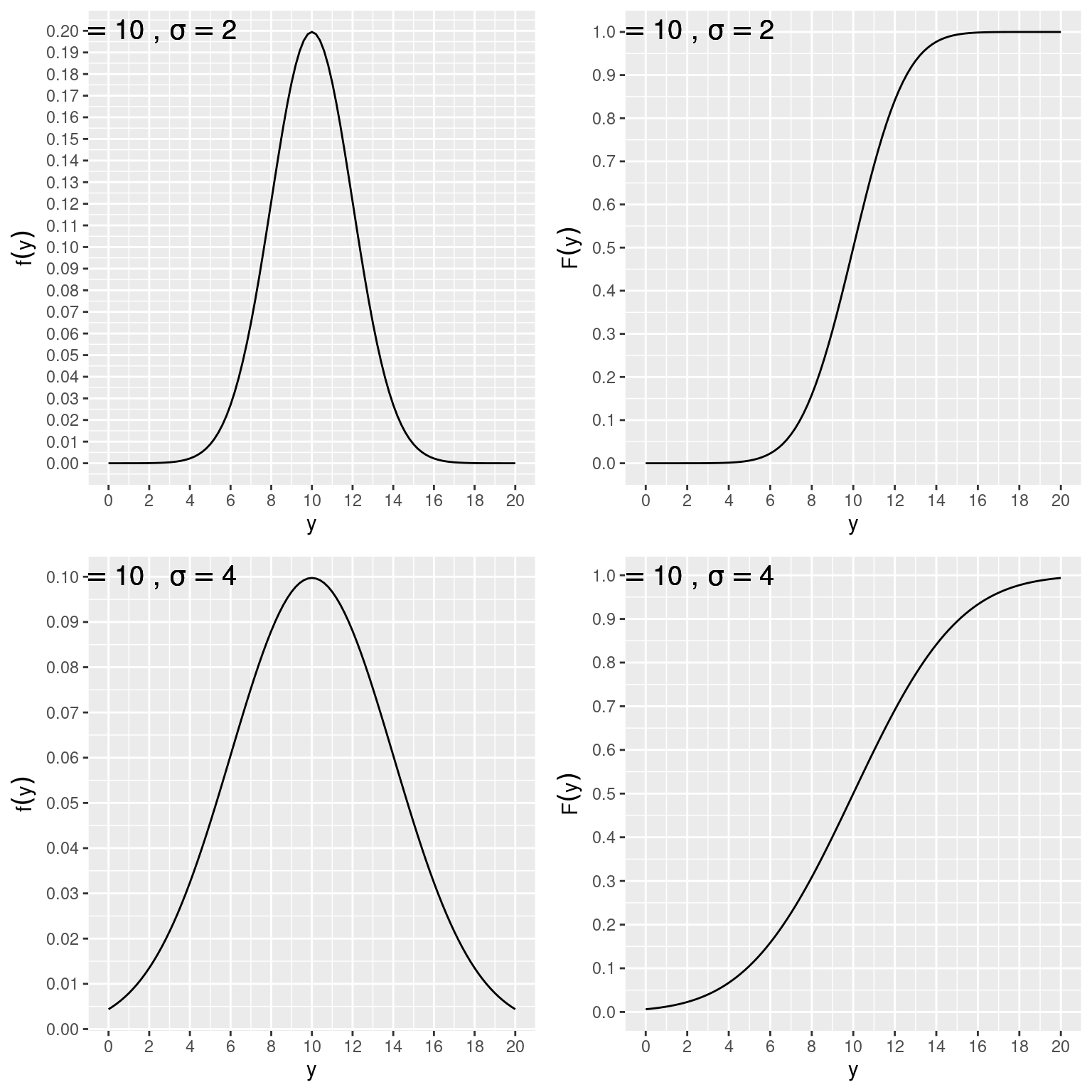
Por exemplo, se o comprimento segue uma distribuição normal com \(\mu = 10\) e \(\sigma = 2\) veremos que a proporção de individuos iguais ou maiores que 16 cm de comprimento é muito baixa, neste caso \(P(Y \ge 16) = 0.0013\). Por outro lado, para \(\sigma = 4\), esperamos encontrar mais indivíduos nos extremos da distribuição em que a proporção de individuos iguais ou maiores que 16 cm seria de \(P(Y \ge 16) = 0.0668\).
31.2 Outros são altamente assimétricos
A distribuição normal, tem um comportamento simétrico, o seja, a proporção de valores acima e abaixo da média é idêntica. Suponha no entando que, ao invés de medir o comprimento dos animais capturados, o experimento coinsista em marcar cada animal, soltá-lo em uma posição conhecida. Futuramente os animais serão recapturados para medirmos a distância de deslocamento. Suponha ainda que a maioria dos indivíduos permaneça próxima ao local de soltura, enquanto outros se desloquem a grandes distâncias. Uma opção mais apropriada para descrever este comportamento poderia ser utilizarmos um Modelo exponencial. Uma variável aleatória que segue um modelo exponencial tem sia função de densidade de probabilidade definida por:
\[f(y|\lambda) = \lambda \times e^{-\lambda y}\]
A expressão acima vale para \(y \ge 0\). Para \(y < 0\), \(f(y) = 0\).
O valor esperado do modelo exponencial é:
\[E(Y) = \mu = \frac{1}{\lambda}\]
enquanto a variância é dada por:
\[VAR(Y) = \sigma^2 = \frac{1}{\lambda^2}\]
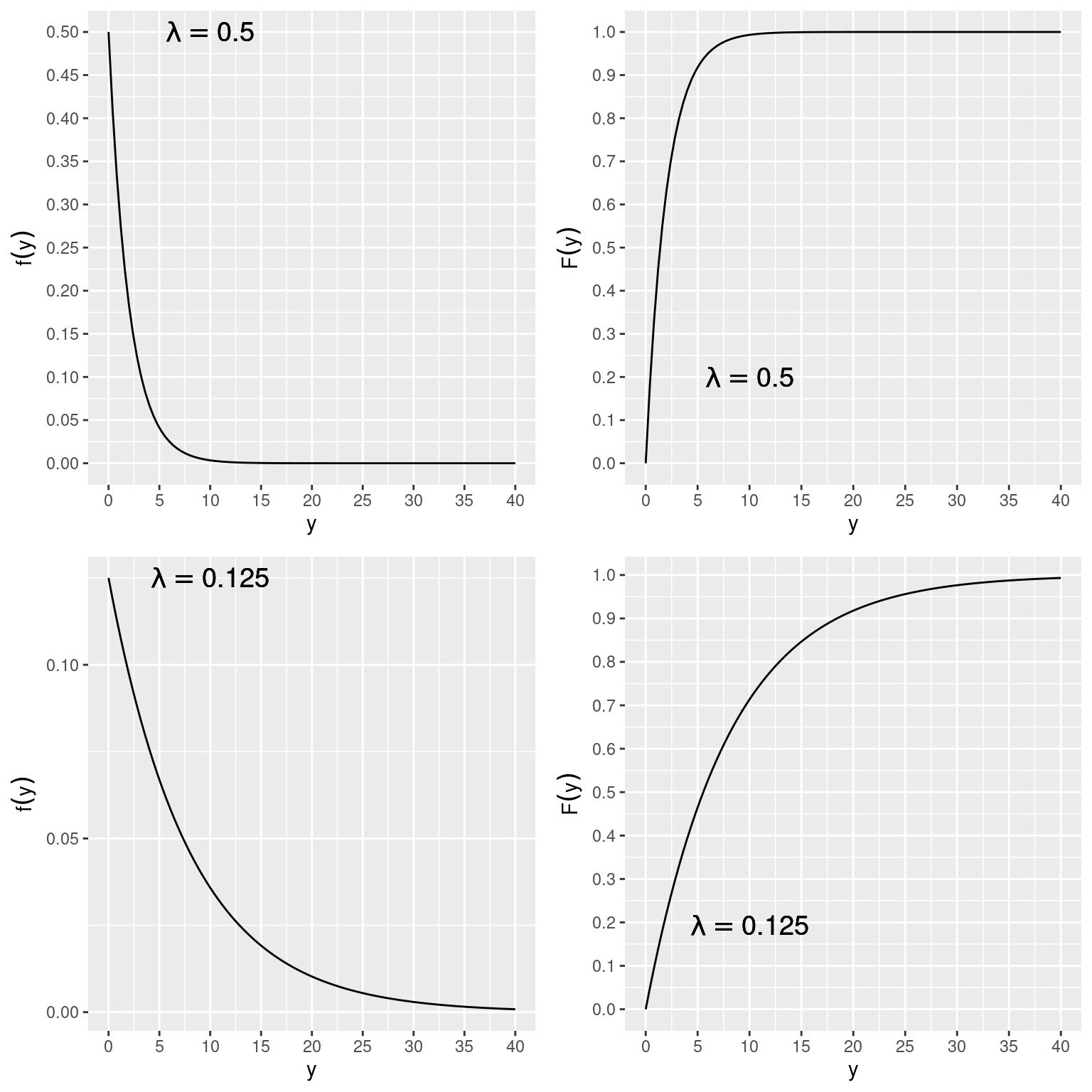
No modelo exponencial, o único parâmetro é \(\lambda\). O modelo é altamente assimétrico, com maior densidade na porção esquerda da curva. Assim, para um fenômeno que possa ser descrito por um modelo exponencial, a maioria das observações será composta de valores baixos, ainda que valores extremamente elevados possam surgir ocasionalmente.