Capítulo 8 Medidas de posição: índice Z
O Índice \(Z\) ou Escore \(Z\) indica a posição de uma observação particular (\(X_i\)). O valor de \(Z\) relaciona a posição de \(X_i\) com a média e o desvio padrão da distribuição. Suponha uma variável com média \(\overline{X}\) e desvio padrão \(s\). O índice de \(Z_i\) para uma observação \(i\) particular é calculado por:
\[Z_i = \frac{X_i - \overline{X}}{s}\]
Seja por exemplo a variável \(X\)
\(X\) = 8.7, 10.4, 8.3, 13.2, 10.7, 8.4, 11, 11.5, 11.2, 9.4, 13, 10.8, 8.8, 5.6, 12.2, 9.9, 10, 11.9, 11.6, 11.2
A média e o desvio padrão são respectivamente \(\overline{X} = 10.39\) e \(s = 1.82\).
O índice \(Z_i\) para a observação \(X_i = 8.3\)
\(Z_i = \frac{8.3 - 10.39}{1.82} = -1.15\)
8.1 Interpretando o valor de \(Z\)
Ao calcularmos o valor de \(Z\) estamos primeiro fazendo uma centralização da variável \(X\) quando subtraímos cada observação \(X_i\) de \(\overline{X}\). A porção \(X_i - \overline{X}\) mede os desvios de cada observação, isto é, suas distâncias (positivas ou negativas) entre \(X_i\) e \(\overline{X}\). Se calcularmos a média destes desvios por exemplo, veremos que o resultado será exatamente zero:
\(\sum_{i=1}^{n}\frac{(X_i - \overline{X})}{n} = 0\)
Portanto, acabamos de centralizar a variável \(X\) ao redor de sua média.
Em seguida dividimos a quantia \(X_i - \overline{X}\) pelo desvio padrão de \(X\) e, ao fazermos, isto estamos padronizando a nova variável que denominaremos de \(Z\). Se calcularmos o desvio padrão desta nova variável veremos que será exatamente igual a \(1\).
Dizemos que o Índice \(Z\) consiste de uma transformação que faz com que a nova variável tenha média = \(0\) e desvio padrão = \(1\).
Um valor de \(Z_i\) particular associado a uma observação \(X_i\) nos indica quantos desvios padrões \(X_i\) está acima ou abaixo da média de seu grupo. A relação entre a nova variável \(Z\) e a variável original \(X\) é:
- Se \(Z_i = 0\), então \(X_i = \overline{X}\);
- Se \(Z_i > 0\), então \(X_i > \overline{X}\);
- Se \(Z_i < 0\), então \(X_i < \overline{X}\);
Para uma distribuição com média igual \(10\) e desvio padrão igual a \(3\) por exemplo, uma observação \(X_i = 16\) terá um valor de \(Z = \frac{16-10}{3} = 2\), indicando que está dois desvios padrões acima da média de \(X\).
Vamos calcular os valores de \(Z\) para a variável \(X\) do exemplo acima e observar os resultados.
| Posicao k | X ordenado | Z ordenado |
|---|---|---|
| 1a Posição | 5.60 | -2.63 |
| 2a Posição | 8.30 | -1.15 |
| 3a Posição | 8.40 | -1.09 |
| 4a Posição | 8.70 | -0.93 |
| 5a Posição | 8.80 | -0.87 |
| 6a Posição | 9.40 | -0.54 |
| 7a Posição | 9.90 | -0.27 |
| 8a Posição | 10.00 | -0.21 |
| 9a Posição | 10.40 | 0.01 |
| 10a Posição | 10.70 | 0.17 |
| 11a Posição | 10.80 | 0.23 |
| 12a Posição | 11.00 | 0.34 |
| 13a Posição | 11.20 | 0.45 |
| 14a Posição | 11.20 | 0.45 |
| 15a Posição | 11.50 | 0.61 |
| 16a Posição | 11.60 | 0.66 |
| 17a Posição | 11.90 | 0.83 |
| 18a Posição | 12.20 | 0.99 |
| 19a Posição | 13.00 | 1.43 |
| 20a Posição | 13.20 | 1.54 |
| Média | 10.39 | 0.00 |
| Desvio padrão | 1.82 | 1.00 |
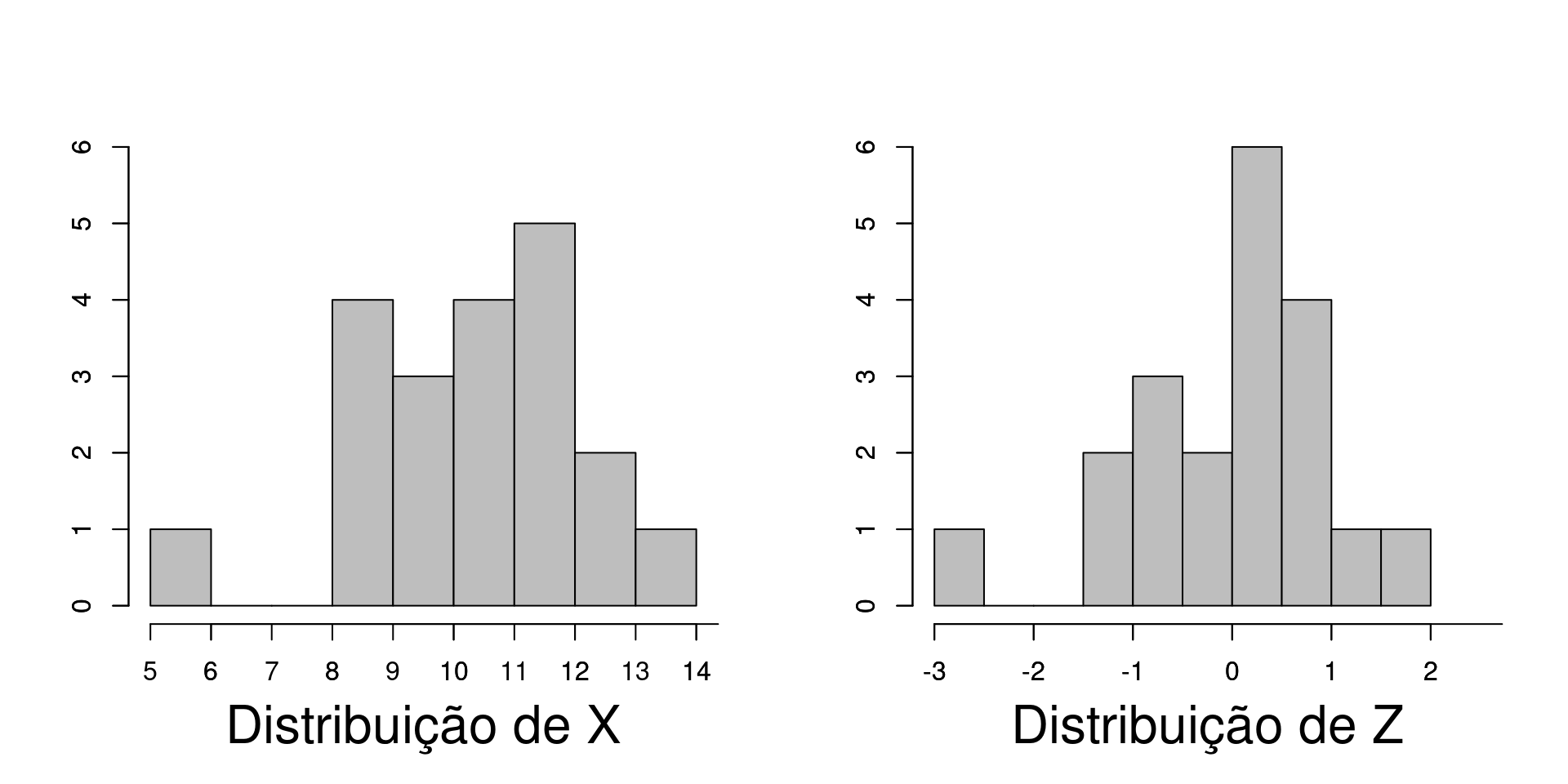
Veja na tabela que conforme o valor de \(X_i\) se distancia da média de \(X = 10.39\), mais distante de zero será o valor de \(Z_i\). Neste exemplo, as observações mais extremas de \(X\) estão, respectivamente, a -2.63 desvios padrões abaixo e 1.54 desvios padrões acima da média. Como discutimos acima, a nova variável \(Z\) tem média \(\overline{Z} = 0\) (está centralizada) e desvio padrão \(1\) (está padronizada).
8.2 Realizando a transformação \(Z\) a partir de uma tabela de dados
Carregue o pacote tidyverse e importe novamente a base de dados Reservatorios_Parana_parcial.csv.
# Carrega pacotes
library(tidyverse)
# Importa base de dados
res = read_delim('Reservatorios_Parana_parcial.csv',
delim = ',',
locale = locale(decimal_mark = '.',
encoding = 'latin1'))Vamos manter somente a variável CPUE e criar outra coluna denominada CPUE_z utilizando a função mutate.
df_z = res %>%
select(CPUE) %>%
mutate(CPUE_z = (CPUE - mean(CPUE))/sd(CPUE))
df_z| CPUE | CPUE_z |
|---|---|
| 9.22 | -0.4723094 |
| 28.73 | 2.1748731 |
| 11.59 | -0.1507398 |
| 30.76 | 2.4503103 |
| 5.95 | -0.9159940 |
| 7.75 | -0.6717640 |
| 7.51 | -0.7043280 |
| 4.01 | -1.1792198 |
| 20.83 | 1.1029745 |
| 2.43 | -1.3935995 |
| 12.55 | -0.0204838 |
| 11.73 | -0.1317442 |
| 13.72 | 0.1382657 |
| 16.50 | 0.5154655 |
| 4.71 | -1.0842414 |
| 7.95 | -0.6446273 |
| 13.12 | 0.0568557 |
| 16.10 | 0.4611921 |
| 11.74 | -0.1303873 |
| 17.95 | 0.7122064 |
| 13.86 | 0.1572614 |
| 13.04 | 0.0460010 |
| 7.35 | -0.7260373 |
| 20.92 | 1.1151860 |
| 13.67 | 0.1314816 |
| 21.82 | 1.2373010 |
| 6.29 | -0.8698617 |
| 9.40 | -0.4478864 |
| 5.60 | -0.9634832 |
| 2.05 | -1.4451592 |
| 24.88 | 1.6524921 |
Se calcularmos a média e desvio padrão das variáveis verermos que CPUE mantém os valores originais, enquanto CPUE_z terá média = \(0\) e desvio padrão = \(1\).
df_z %>%
summarize(CPUE_media = mean(CPUE),
CPUE_dp = sd(CPUE),
CPUE_z_media = round(mean(CPUE_z),2),
CPUE_z_dp = round(sd(CPUE_z),2))| CPUE_media | CPUE_dp | CPUE_z_media | CPUE_z_dp |
|---|---|---|---|
| 12.70097 | 7.3701 | 0 | 1 |
8.3 Valores esperados de \(Z\) em uma distribuição normal padronizada
A interpretação de \(Z\) faz sentido quando desejamos posicionar uma determinada observação \(X_i\) como função da média e desvio padrão de seu grupo. Veremos nos capítulos 14 e 15 que se uma variável \(X\) puder ser descrita adequadamente por uma Distribuição Normal de probabilidades, uma regra empírica nos permite determinar qual o percentual das observações está acima e abaixo de alguns limites conhecidos.
Na figura abaixo vemos estes limites para uma distribuição normal teórica. Suponha que tomemos uma observação ao acaso desta distribuição. Existe uma probabilidade de aproximadamente \(68\%\) de que esta observação esteja entre os limites de \(-1\) e \(+1\) desvios padrões da média. Ou ainda, existe uma probabilidade de aproximadamente \(95\%\) de que esta observação esteja entre \(-2\) e \(+2\) desvio padrões da média. Por outro lado, que é muito improvável amostrarmos um valor a mais de \(3\) desvios padrões distantes da média. Isto deverá ocorrer em somente de cerca de \(0,2\%\) dos casos em que sortearmos uma amostra aleatoriamente.
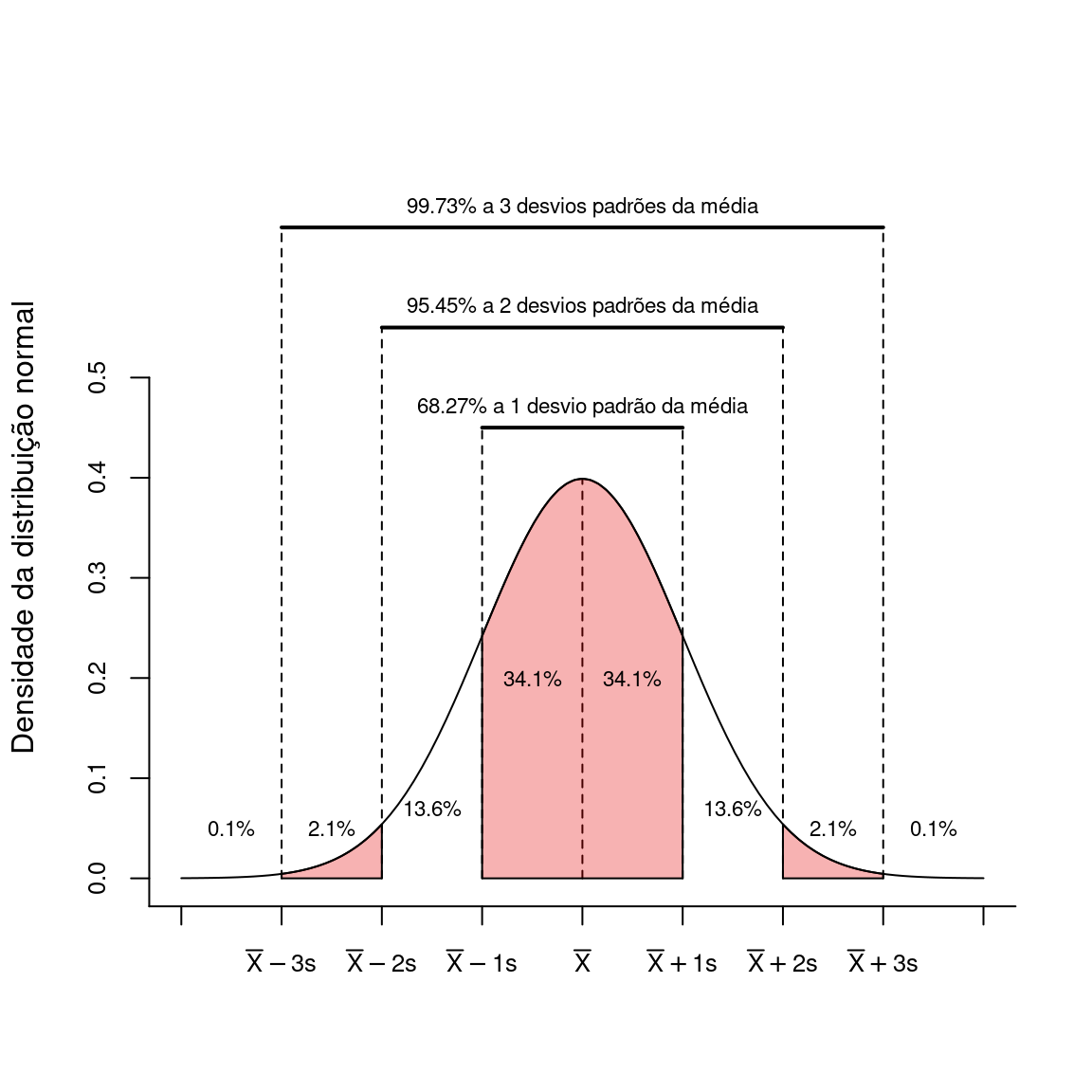
Este assunto será abordado em mais detalhes na seção sobre inferência estatística (Capítulos 12 a 18). Por hora, suponha que a distribuição de altura de homens adultos siga uma distribuição normal com média \(\mu = 175\) cm e desvio padrão de \(\sigma = 175\) cm.
Neste caso, se tomarmos os limites entre \(-2\) e \(+2\) desvios padrões teremos:
\(\mu - 2 \times \sigma = 175 - 2 \times 10 = 155\) cm
e
\(\mu + 2 \times \sigma = 175 + 2 \times 10 = 195\) cm
Sugerindo que somente cerca de \(5\%\) dos homens adultos teriam mais de \(195\) cm ou menos de \(155\) cm de altura.
Os processos centralização e padronização de uma variável são úteis em diferentes momentos da estatística descritiva e inferencial. Veremos este processo aparecendo novamente quando formos medir a associação entre variáveis quantitativas por meio do coeficiente de correlação de Pearson (Capítulo 10) e também quando formos falar sobre associação entre variáveis quantitativas e qualitativas no capítulo 11.