Capítulo 28 Probabilidade condicional e independência
Voltemos ao experimento “virar uma estrutura e contar o número de itens” com o espaço amostral:
\(\Omega = \{(F0), (F1), (F2), (F3), (F4), (F5), (F6), (G0), (G1), (G2), (G3), (G4)\}\)
Os eventos \(A\) “virar uma folha”:
\(A = \{(F0), (F1), (F2), (F3), (F4), (F5), (F6)\}\)
E \(B\) “encontar mais de 3 itens”:
\(B = \{(F3), (F4), (F5), (F6), (G3), (G4)\}\)
Representados no diagrama de Venn abaixo.
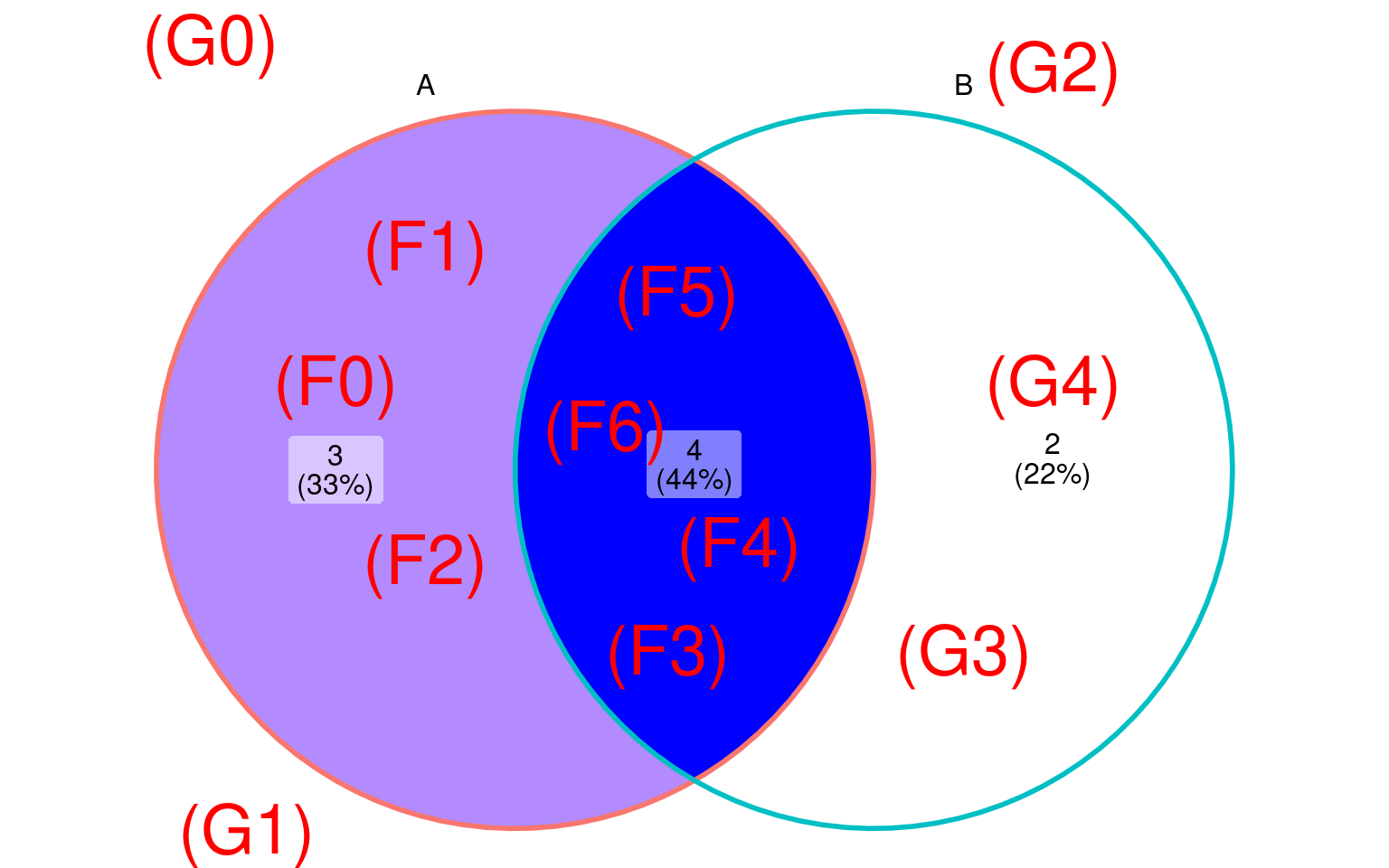
Nos capítulos anteriores obtivemos as probabilidades \(P(A)\), \(P(B)\), \(P(A \cup B)\) e \(P(A \cap B)\). Digamos agora que, ao virar uma estrutura, sabemos que a estrutura era uma folha. A pergunta é:
Qual a probabilidade de que tenham sido obtidos mais de 3 itens?
Ao informarmos que a estrutura era uma folha, sabemos que nem todos os eventos de \(\Omega\) podem ter ocorrido. Neste exemplo, somente as 7 observações do evento e \(A\) consistem de uma folha:
Destas, apenas 4 possuem mais de 3 itens, de modo a resposta à pergunta seria \(\frac{4}{7}\). Este resultado é conhecido como probabilidade condicional, denotada pelo símbolo (\(|\)). Neste exemplo específico estamos perguntando:
Dado que \(A\) OCORREU, qual a probabilidade de que \(B\) tenha ocorrido? Simbolicamente, esta questão é escrita como \(P(B|A)\).
\[P(B|A) = \frac{4}{7} = 0.57\]
Esta probabilidade condicional foi calculada pelo número de observações favoráveis à intersecção de \(A\) e \(B\) (\(\#A \cap B\)) relativa ao número de observações do evento \(A\) (\(\#A\)). Isto significa ao sabermos parte dos resultados, o espaço amostral inicial inicial foi reduzido, neste caso, ao espaço coincidente com \(A\). Portanto, temos que:
\[P(B|A) = \frac{\#A \cap B}{\#A}\]
Se dividirmos ambos o numerador e o denominador da expressão acima pelo tamanho do espaço amostral (\(\#\Omega\)) teremos:
\[P(B|A) = \frac{\frac{\#A \cap B}{\#\Omega}}{\frac{\#A}{\#\Omega}}\]
Como \(\frac{\#A \cap B}{\#\Omega} = P(A \cap B)\) e \(\frac{\#A}{\#\Omega} = P(A)\), uma expressão simples para a probabilidade condicional será:
\[P(B|A) = \frac{P(A \cap B)}{P(A)}\]
Esta expressão nos dá também uma forma de calcularmos a probabilidade da intersecção de \(A\) com \(B\). No capítulo 27 esta probabilidade foi obtida contando o número de eventos na intersecção dividido pelo tamanho do espaço amostral. No entanto, podemos calculá-la diretamente por:
\[P(B \cap A) = P(A) \times P(B|A)\]
Obs: faça os cálculos para \(P(A \cap B)\) utilizando a expressão acima e veja se coincide com o obtido no capítulo 27.
Uma vez que probabilidade condicional se refere ao cálculo de probabilidades em eventos complexos sequenciais, podemos fazer a mesma representação de um experimento complexo utilizando um diagrama de árvore onde estão indicadas as probabilidades de ocorrência de cada evento, bem como as probabilidades condicionais.
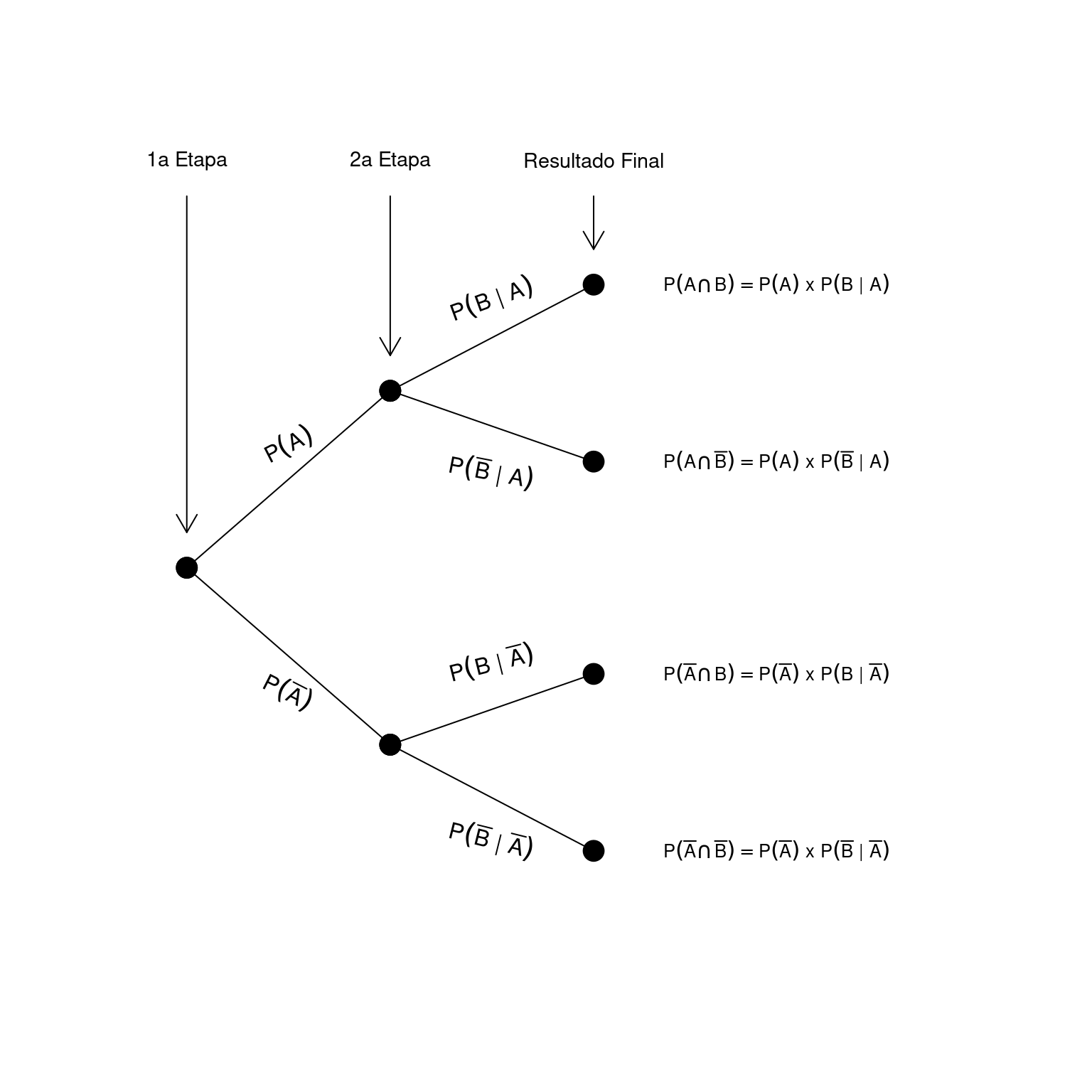
Neste esquema, podemos ler as probabilidades de obtenção de cada resultado da seguinte forma. A primeira etapa do experimento, pode resultar na ocorrencia do evento \(A\) com probabilidade \(P(A)\), ou de seu complemento, com probabilidade \(P(\overline{A})\). Na segunda etapa, os resultados podem ser dar da seguinte forma:
- Dado que \(A\) ocorreu:
- \(B\) pode ocorrer com probabilidade \(P(B|A)\). Neste caso, a ocorrência de \(A\) e \(B\) será dada por \(P(A \cap B) = P(A) \times P(B|A)\);
- o complemento de \(B\) pode ocorrer com probabilidade \(P(\overline{B}|A)\). Neste caso, a ocorrência de \(A\) e \(\overline{B}\) será dada por \(P(A \cap \overline{B}) = P(A) \times P(\overline{B}|A)\);
- Dado que \(\overline{A}\) ocorreu:
- \(B\) pode ocorrer com probabilidade \(P(B|\overline{A})\). Neste caso, a ocorrência de \(\overline{A}\) e \(B\) será dada por \(P(\overline{A} \cap B) = P(\overline{A}) \times P(B|\overline{A})\);
- o complemento de \(B\) pode ocorrer com probabilidade \(P(\overline{B}|\overline{A})\). Neste caso, a ocorrência de \(\overline{A}\) e \(\overline{B}\) será dada por \(P(\overline{A} \cap \overline{B}) = P(\overline{A}) \times P(\overline{B}|\overline{A})\);
Estas ocorrências denotam as probabilidades de todos os eventos possíveis para este experimento.
Vamos expressar numericamente todas as probabilidades representadas no diagrama de árvore acima:
REFAZER DIAGRAMA DE ÁRVORE. Função ‘bayes_probability_tree()’ desatualizada
Obs.: Refaça os cálculos e confira os resultados
28.1 Eventos independentes
Vamos retomar todas as probabilidades do experimento deste capítulo: “virar uma estrutura e contar o número de itens”. As probabilidades de cada evento \(A\), \(B\) e de seus complementos são:
\(P(A) = 0.58\)
\(P(\overline{A}) = 0.42\)
\(P(B) = 0.5\)
\(P(\overline{B}) = 0.5\)
Embora a probabilidade de ocorrencia de \(B\) seja 0.5, a discussão sobre probabilidade condicional nos informa que ao sabermos que \(A\) ocorreu, o conhecimento sobre \(B\) deve ser atualizado para \(P(B|A)\), que em nosso exemplo será 0.57.
Note que a nova estimativa da probabilidade de \(B\) está condicionada ao conhecimento prévio sobre a ocorrência de \(A\). Portanto dizemos que \(A\) e \(B\) são eventos dependentes, de modo que \(P(B) \neq P(B|A)\).
28.1.1 Um exemplo de eventos independentes
Dois eventos são ditos independentes se a informação sobre a ocorrência de um não altera a probabilidade condicional da ocorrência do outro, de modo que \(P(B) = P(B|A)\).
Suponha em um estudo sobre o perfil de visitação em uma área de preservação ambiental, tenham sido avaliados a idade (até 20 ou acima de 20 anos) e a região de origem do visitante (da própria cidade ou de outra cidade). Foram investigadas ao todo 600 pessoas com os seguintes perfis:
| Da cidade | De fora da cidade | |
|---|---|---|
| Até 20 | 30 | 170 |
| Mais de 20 | 60 | 340 |
Vamos denominar de:
\(A\): ter até 20 anos e \(\overline{A}\): ter mais de 20 anos.
\(B\): ser da cidade e \(\overline{B}\): ser de fora da cidade.
Neste caso a tabela fica:
\(P(A) = \frac{30 + 170}{600} = \frac{200}{600} \approx 0.33\)
\(P(\overline{A}) = \frac{60 + 340}{600} = \frac{400}{600} \approx 0.67\)
\(P(B) = \frac{30 + 60}{600} = \frac{90}{600} = 0.15\)
\(P(\overline{B}) = \frac{30 + 340}{600} = \frac{510}{600} = 0.85\)
Se soubermos por exemplo que a pessoa tem mais de 20 anos, a probabilidade condicional de ser da cidade é de:
\(P(B|A) = \frac{60}{60 + 340} = \frac{60}{400} = 0.15\)
Vemos que \(P(B) = P(B|A) = 0.85\) de modo que informar se uma pessoa tem ou não mais de 20 anos não nos diz nada sobre se a pessoa é da cidade ou não. Portanto, a classe de idade neste caso é independente da origem do visitante.
28.2 Eventos independentes vs mutuamente exclusivos
Uma questão comum em tópicos de probabilidade é a confusão entre os conceitos de eventos mutuamente exclusivos e de eventos independentes. Inicialmente vamos às definições:
- A união de eventos é dada por:
\(P(A \cup B) = P(A) \times P(B) \times P(A \cap B)\)
- Quando dois eventos são mutuamente exclusivos não há intersecção e consequentemente:
\(P(A \cap B) = 0\)
de modo que,
\(P(A \cup B) = P(A) \times P(B)\)
Eventos mutuamente exclusivos são representados no diagrama de Venn abaixo.
- Quando dois eventos são independentes:
\(P(A \cap B) = P(A) \times P(B)\)
Se ambos \(P(A)\) e \(P(B)\) são diferentes de zero, esta definição não permite que dois eventos sejam simultaneamente independentes E mutuamente exclusivos, pois para eventos independentes \(P(A \cap B)\) será zero somente se \(P(A)\) ou \(P(B)\) forem zero.
- Vamos agora à ideia da probabilidade condicional quando dos eventos são dependentes. Neste caso temos que:
\(P(A \cap B) = P(A) \times P(B|A)\)
Esta relação expressa a ideia que ao informar sobre a ocorrência de \(A\), a probabilidade sobre a ocorrência de \(B\) deve ser atualizada de \(P(B)\) para \(P(B|A)\).
Deste modo, para dois eventos dependentes, \(P(B) \ne P(B|A)\).
- Finalmente, vamos associar a ideia de dependência com a ideia de eventos mutuamente exclusivos. Se sabemos que dois eventos são mutuamente exclusivos, então sabemos que ao ocorrer um deles, o outro não poderá ocorrer, ou seja, dado que \(A\) ocorreu temos certeza de que \(B\) não poderá ocorrer, de modo que \(P(B|A) = 0\).
Representando eventos mutuamente exclusivos em um diagrama de árvore teremos:
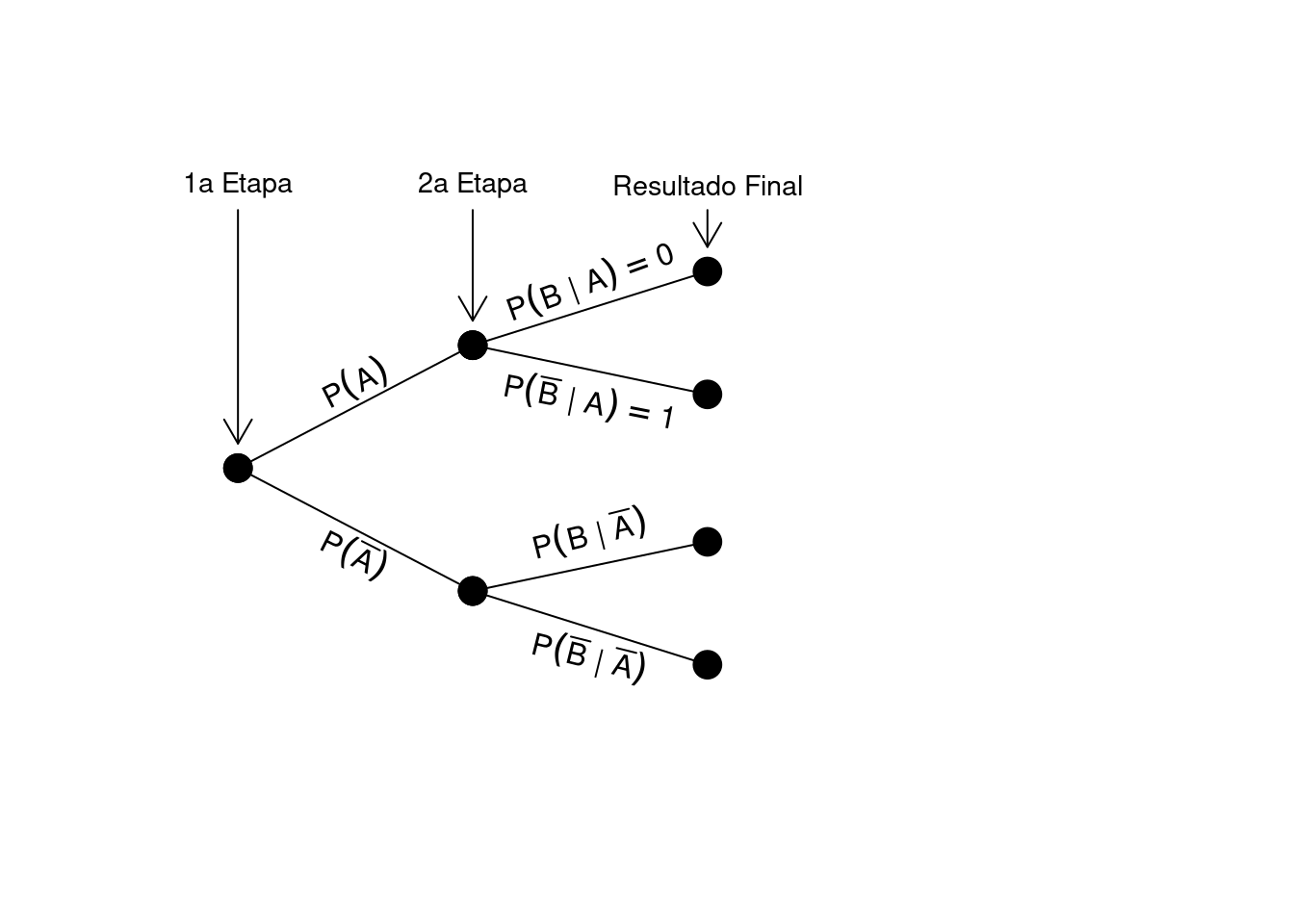
Ao saber que \(A\) ocorreu, veja que \(P(B|A)\) tem probabilidade igual a zero, de modo que eventos mutuamente exclusivos são necessariamente dependentes.
- O que ocorre se os eventos não são mutuamente exclusivos, ou seja, se \(P(A \cap B) \ne 0\)? Neste caso \(A\) e \(B\) podem ou não ser independentes e a resposta dependerá se:
- \(P(B) = P(B|A)\) (eventos independentes) ou;
- \(P(B) \ne P(B|A)\) (eventos dependentes).