Capítulo 3 Descrevendo variáveis qualitativas

Variáveis qualitativas podem ser categóricas não-ordenadas ou categóricas ordenadas. A descrição de variáveis desta natureza se dá por meio da contagem e da representação dos níveis destas variáveis por meio da contagem total, pelos valores relativos ou percentuais.

Carregue o pacote tidyverse e importe novamente a base de dados Reservatorios_Parana_parcial.csv.

# Carrega pacotes
library(tidyverse)
# Importa base de dados 
res = read_delim('Reservatorios_Parana_parcial.csv',
                  delim = ',',
                  locale = locale(decimal_mark = '.',
                                  encoding = 'latin1'))

Na tabela, temos 3 variáveis categóricas: Reservatorio, Bacia e Trofia. A primeira identifica cada reservatório pelo seu nome. A segunda é uma variável categórica não-ordenada (nível de mensuração nominal) e a terceira uma variável categórica ordenada (nível de mensuração ordinal).

3.1 Representação em tabelas de frequência

Como discutimos no capítulo 1, se uma variável é descrita no nível de mensuração nominal, como é o caso de Bacia, nossa única ação possível é a contagem da frequência com que cada um dos níveis aparece na variável. Essa contagem pode ser obtda por meio de uma tabela de frequências.

fbacia = res %>% 
  group_by(Bacia) %>% 
  summarise(Frequencia = n())

fbacia

Bacia	Frequencia
Iguacu	13
Ivai	2
Litoranea	4
Paranapanema	7
Piriqui	2
Tibagi	3

O resultado mostra que existem 13 reservatórios na tabela pertancentes à bacia do rio 13, 2 à bacia do rio 2 e assim por diante.

As linhas da tabela estão organizadas em ordem alfabética. Como esata é uma variável não-ordenada, isto em sí não é um problerma. No entanto, para facilitar a visualização, podemos ordená-las de modo decrescente como função do número de reservatórios por bacia:

fbacia = fbacia %>% 
  arrange(desc(Frequencia))

fbacia

Bacia	Frequencia
Iguacu	13
Paranapanema	7
Litoranea	4
Tibagi	3
Ivai	2
Piriqui	2

Podemos olhar também para a frequência relativa do número de reservatórios por bacia.

fbacia_rel = fbacia %>% 
  mutate(Freq_relativa = Frequencia / sum(Frequencia))

fbacia_rel

Bacia	Frequencia	Freq_relativa
Iguacu	13	0.4193548
Paranapanema	7	0.2258065
Litoranea	4	0.1290323
Tibagi	3	0.0967742
Ivai	2	0.0645161
Piriqui	2	0.0645161

A característica da frequência relativa, é que o somatório da coluna deve ser igual a \(1\), enquanto a frequência numérica tem o somatório igual ao número de linhas na tabela.

## # A tibble: 1 × 2
##   Frequencia Freq_relativa
##        <int>         <dbl>
## 1         31             1

3.2 Tabelas de frequência para variáveis categóricas ordenadas

A característica da variável Trofia difere da anterior unicamente por ser uma variável categórica ordenada que no caso, expressa o grau de eutrofização dos reservatórios. Neste sentido, a única mudança na representação da variável se deve ao fato de que existe uma sequência natural para representar os níveis. Podemos indicar que uma determinada variável é categórica ordenada fazendo uma pequena alteração na base de dados.

Se montarmos uma tabela de frequência da variável trofia, teremos as linhas organizadas em ordem alfabética:

ftrofia = res %>% 
  group_by(Trofia) %>% 
  summarise(Frequencia = n())

ftrofia

Trofia	Frequencia
Eutrófico	2
Mesotrófico	3
Oligotrófico	24
NA	2

Se desejarmos que as colunas apareçam como função do nível de Eutrofização, devemos primeiro transformar a variável bacia em um fator ordenado que é o modo como o R interpreta uma variável categórica ordenada.

Use o comando:

glimpse(res)

## Rows: 31
## Columns: 11
## $ Reservatorio  <chr> "Cavernoso", "Curucaca", "Foz do Areia", "Irai", "JMF", …
## $ Bacia         <chr> "Iguacu", "Iguacu", "Iguacu", "Iguacu", "Iguacu", "Iguac…
## $ Fechamento    <dbl> 1965, 1982, 1980, 2000, 1970, 1996, 1978, 1979, 1998, 19…
## $ Area          <dbl> 2.90, 2.00, 139.00, 15.00, 0.45, 3.40, 14.00, 3.30, 124.…
## $ Trofia        <chr> "Oligotrófico", "Oligotrófico", "Oligotrófico", "Eutrófi…
## $ pH            <dbl> 7.4, 7.0, 7.3, 6.9, 7.3, 7.1, 8.8, 7.1, 7.3, 6.5, 8.6, 9…
## $ Condutividade <dbl> 33.1, 32.4, 35.5, 50.2, 40.2, 23.7, 125.6, 22.8, 39.6, 2…
## $ Alcalinidade  <dbl> 139.80, 125.70, 97.00, 3.30, 3.70, 152.70, 526.00, 50.67…
## $ P.total       <dbl> 7.8, 4.7, 14.3, 53.4, 41.2, 3.3, 15.2, 4.5, 12.1, 11.0, …
## $ Riqueza       <dbl> 18, 16, 19, 12, 18, 17, 11, 8, 21, 8, 24, 21, 22, 15, 10…
## $ CPUE          <dbl> 9.22, 28.73, 11.59, 30.76, 5.95, 7.75, 7.51, 4.01, 20.83…

para verificar que o R entende a variável Trofia como um character (<chr>).

Iremos transformar esta variável para que o R a interprete como uma variável categórica ordenada fazendo:

res = res %>% 
  mutate(Trofia = factor(Trofia, ordered = TRUE, 
                         levels = c('Oligotrófico', 'Mesotrófico', 'Eutrófico')))

Após aplicarmos este comando, vemos que agora o R reconhece esta variável como do tipo <ord>:

glimpse(res)

## Rows: 31
## Columns: 11
## $ Reservatorio  <chr> "Cavernoso", "Curucaca", "Foz do Areia", "Irai", "JMF", …
## $ Bacia         <chr> "Iguacu", "Iguacu", "Iguacu", "Iguacu", "Iguacu", "Iguac…
## $ Fechamento    <dbl> 1965, 1982, 1980, 2000, 1970, 1996, 1978, 1979, 1998, 19…
## $ Area          <dbl> 2.90, 2.00, 139.00, 15.00, 0.45, 3.40, 14.00, 3.30, 124.…
## $ Trofia        <ord> Oligotrófico, Oligotrófico, Oligotrófico, Eutrófico, Mes…
## $ pH            <dbl> 7.4, 7.0, 7.3, 6.9, 7.3, 7.1, 8.8, 7.1, 7.3, 6.5, 8.6, 9…
## $ Condutividade <dbl> 33.1, 32.4, 35.5, 50.2, 40.2, 23.7, 125.6, 22.8, 39.6, 2…
## $ Alcalinidade  <dbl> 139.80, 125.70, 97.00, 3.30, 3.70, 152.70, 526.00, 50.67…
## $ P.total       <dbl> 7.8, 4.7, 14.3, 53.4, 41.2, 3.3, 15.2, 4.5, 12.1, 11.0, …
## $ Riqueza       <dbl> 18, 16, 19, 12, 18, 17, 11, 8, 21, 8, 24, 21, 22, 15, 10…
## $ CPUE          <dbl> 9.22, 28.73, 11.59, 30.76, 5.95, 7.75, 7.51, 4.01, 20.83…

E se fizermos:

res$Trofia

##  [1] Oligotrófico Oligotrófico Oligotrófico Eutrófico    Mesotrófico 
##  [6] Oligotrófico Oligotrófico Oligotrófico Oligotrófico Oligotrófico
## [11] Oligotrófico Oligotrófico Oligotrófico Oligotrófico Mesotrófico 
## [16] Oligotrófico Oligotrófico Oligotrófico Mesotrófico  Oligotrófico
## [21] Oligotrófico Oligotrófico Oligotrófico <NA>         Oligotrófico
## [26] Oligotrófico Eutrófico    Oligotrófico Oligotrófico <NA>        
## [31] Oligotrófico
## Levels: Oligotrófico < Mesotrófico < Eutrófico

Temos agora a indicação de que: Oligotrófico < Mesotrófico < Eutrófico, expressando a sequência que definimos para esta variável ordinal.

A partir de agora, se extrairmos uma tabela de frequência relativa, as linhas apareceram na ordem pré-definida.

ftrofia = res %>% 
  group_by(Trofia) %>% 
  summarise(Frequencia = n())

ftrofia

Trofia	Frequencia
Oligotrófico	24
Mesotrófico	3
Eutrófico	2
NA	2

Caso você não queira representar os dados faltantes (NA), é possível utilizar a função drop_na() para excluir linhas com NAs.

# Exclui linhas da tabela referentes aos dados faltantes em `Trofia`
ftrofia = res %>% 
  drop_na(Trofia) %>% 
  group_by(Trofia) %>% 
  summarise(Frequencia = n())

ftrofia

Trofia	Frequencia
Oligotrófico	24
Mesotrófico	3
Eutrófico	2

Podemos adicionar uma uma coluna de frequência relativa como fizemos anteriormente.

ftrofia_rel = ftrofia %>% 
  mutate(Freq_relativa = Frequencia / sum(Frequencia))

ftrofia_rel

Trofia	Frequencia	Freq_relativa
Oligotrófico	24	0.8275862
Mesotrófico	3	0.1034483
Eutrófico	2	0.0689655

3.3 Representação gráfica

Variáveis categóricas não-ordenadas ou ordenadas podem ser representadas por gráficos de barras.

Utilizaremos o pacote ggplot2 para representar graficamente as variáveis. O ggplot2 é instalado e habilitado juntamente com o tidyverse, de modo que neste momento você já o tem habilitado em sua seção do R.

Para uma rápida explicação do ggplot2 veja aqui. Para uma explicação detalhada veja o site oficial (ggplot2) e o livro ggplot2: Elegant Graphics for Data Analysis.

3.3.1 Criando um gráfico no ggplot2

Um gráfico no ggplot2 é feito em camadas que devem ter minimamente: a definição da tabela de dados, a estética gráfica (quais serão as variáveis envolvidas e suas posições no gráficos) e o formato (gráficos de pontos, linhas, barras, etc.). Esta abordagem permite que tenhamos um método consistente para construir diferentes tipos gráficos.

Gráfico de frequência

Um gráfico de barras da variável Bacia ficaria:

ggplot(data = res) +
  aes(x = Bacia) +
  geom_bar()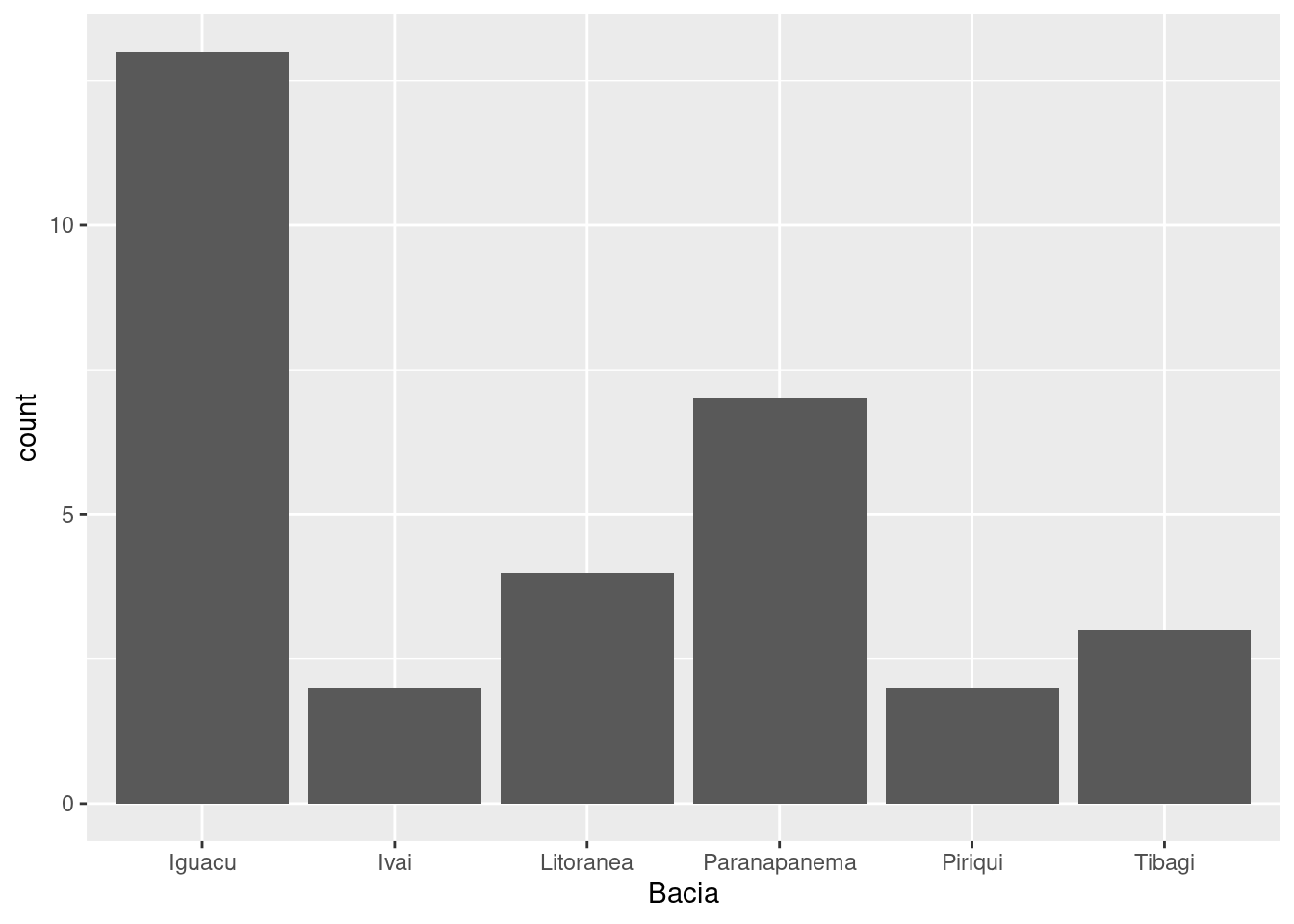

Vamos entender o comando:

• ggplot(res): define a tabela de dados que será utilizada.

• aes(x = Bacia): define que o eixo \(x\) deste gráfico deverá contém os níveis da variável Bacia.

• geom_bar(): define o tipo gráfico (no ggplot2 é denominado de geometria gráfica)

Estes argumentos devem ser inseridos sequencialmente separtados pelo símbolo +.

O argumento geom_bar() espera como argumento uma variável qualitativa em um dos eixos e, por padrão, fará a contagem dos níveis dentro da variável e apresentará esta contagem no outro eixo.

Deste modo, poderíamos ter feito o mesmo gráfico de barras indicando que a variável Bacia seria representada no eixo \(y\) o que resultaria em um gráfico de barras invertido conforme abaixo:

ggplot(data = res) +
  aes(y = Bacia) +
  geom_bar()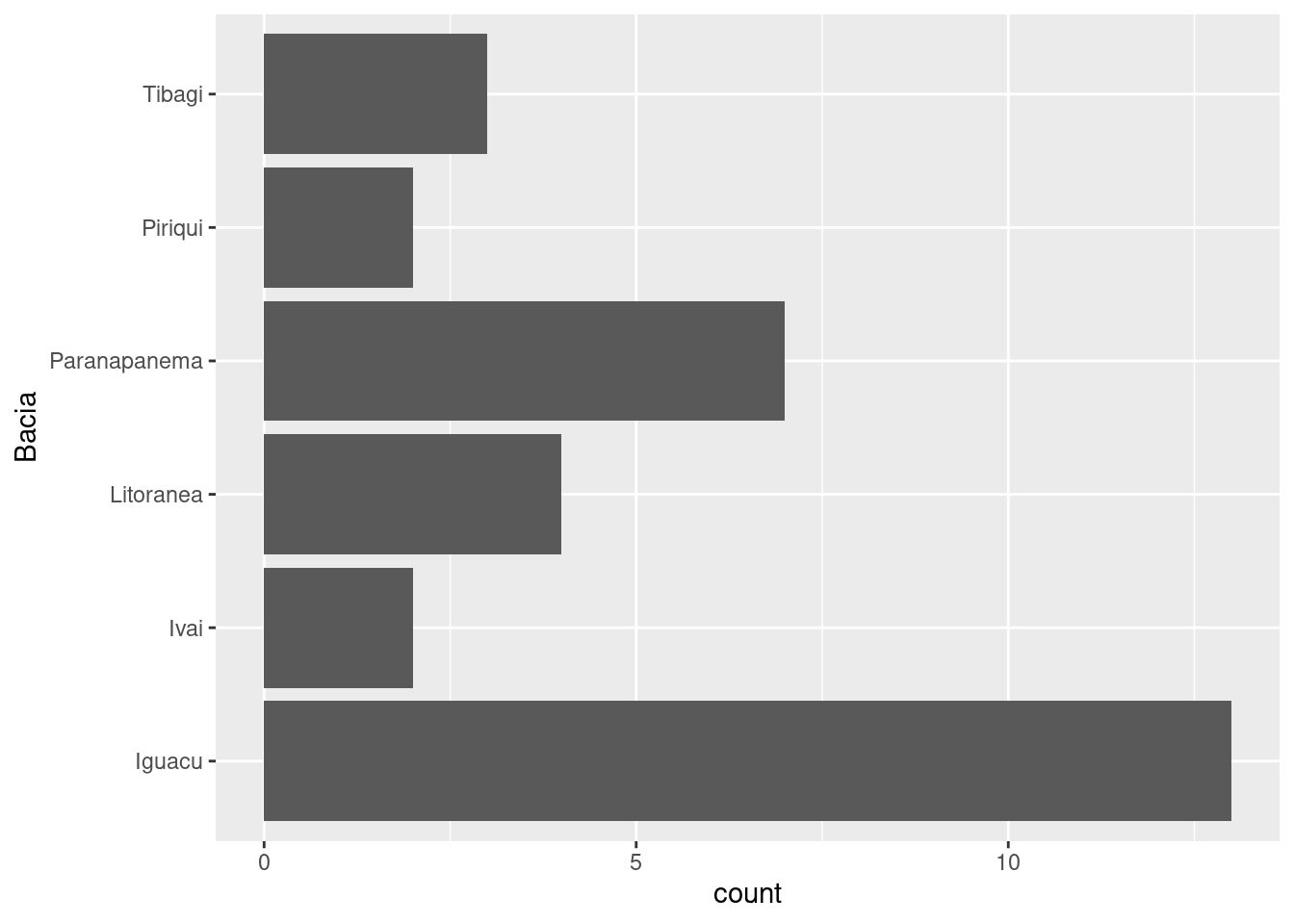

A estética gráfica (comando aes()) não precisa estar em uma linha separada. Também não é obrigatório escrevermos data = res. De fato, é mais comun escrevermos esta sequência de argumentos como:

ggplot(res, mapping = aes(x = Bacia)) +
  geom_bar()

ou simplesmente:

ggplot(res, aes(x = Bacia)) +
  geom_bar()

Finalmente, poderíamos organizar os barras em ordem decrescente como fizemos com as tabelas de frequência, utilizando a função fct_infreq():

ggplot(res, aes(x = fct_infreq(Bacia))) +
  geom_bar()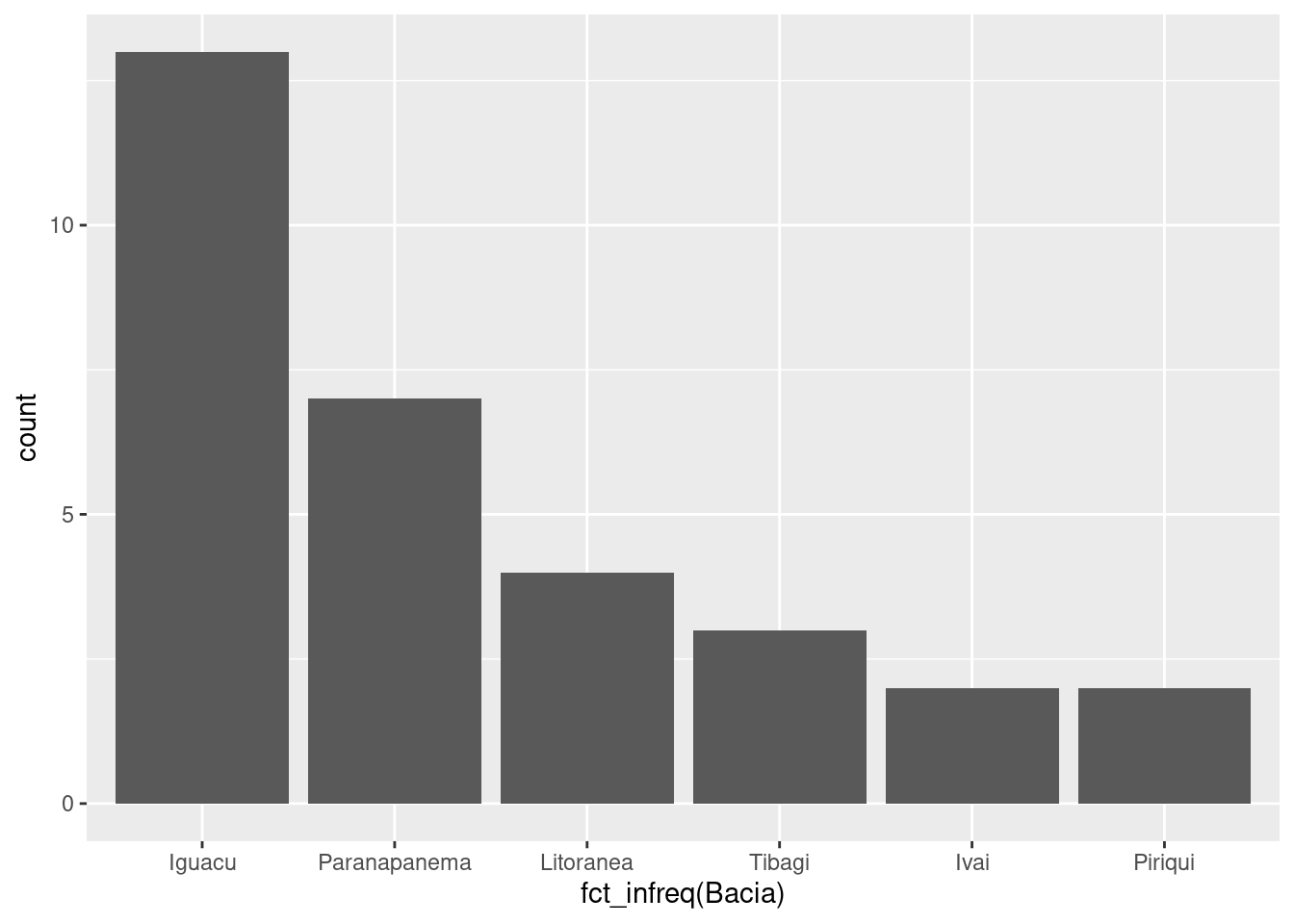

ou em ordem crescente revertendo o comando anterior, com a função fct_rev().

ggplot(res, aes(x = fct_rev(fct_infreq(Bacia)))) +
  geom_bar()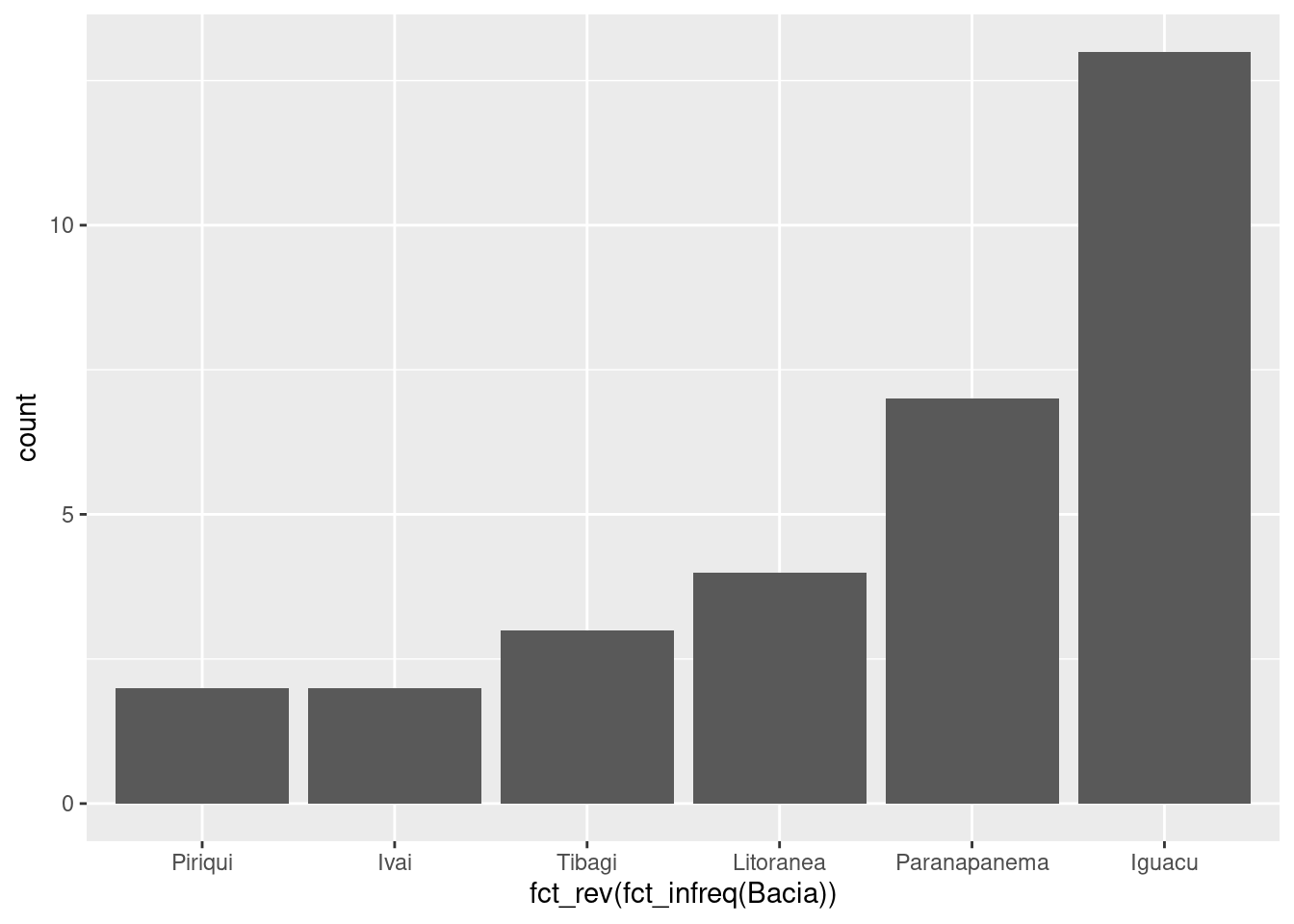

Formatanto a figura

Para tormar a figura mais auto-explicativa, podemos adicionar camadas identificando os eixos e fornecendo, título, subtítulo e outras informações:

ggplot(res, aes(x = Bacia)) +
  geom_bar() +
  labs(title = 'Reservatórios do Estado do Paraná',
       subtitle = 'Reservatórios por bacia hidrográfica',
       caption = 'Dados obtidos do livro: Biocenoses em Reservatórios',
       x = 'Bacia hidrográfica',
       y = 'Frequência')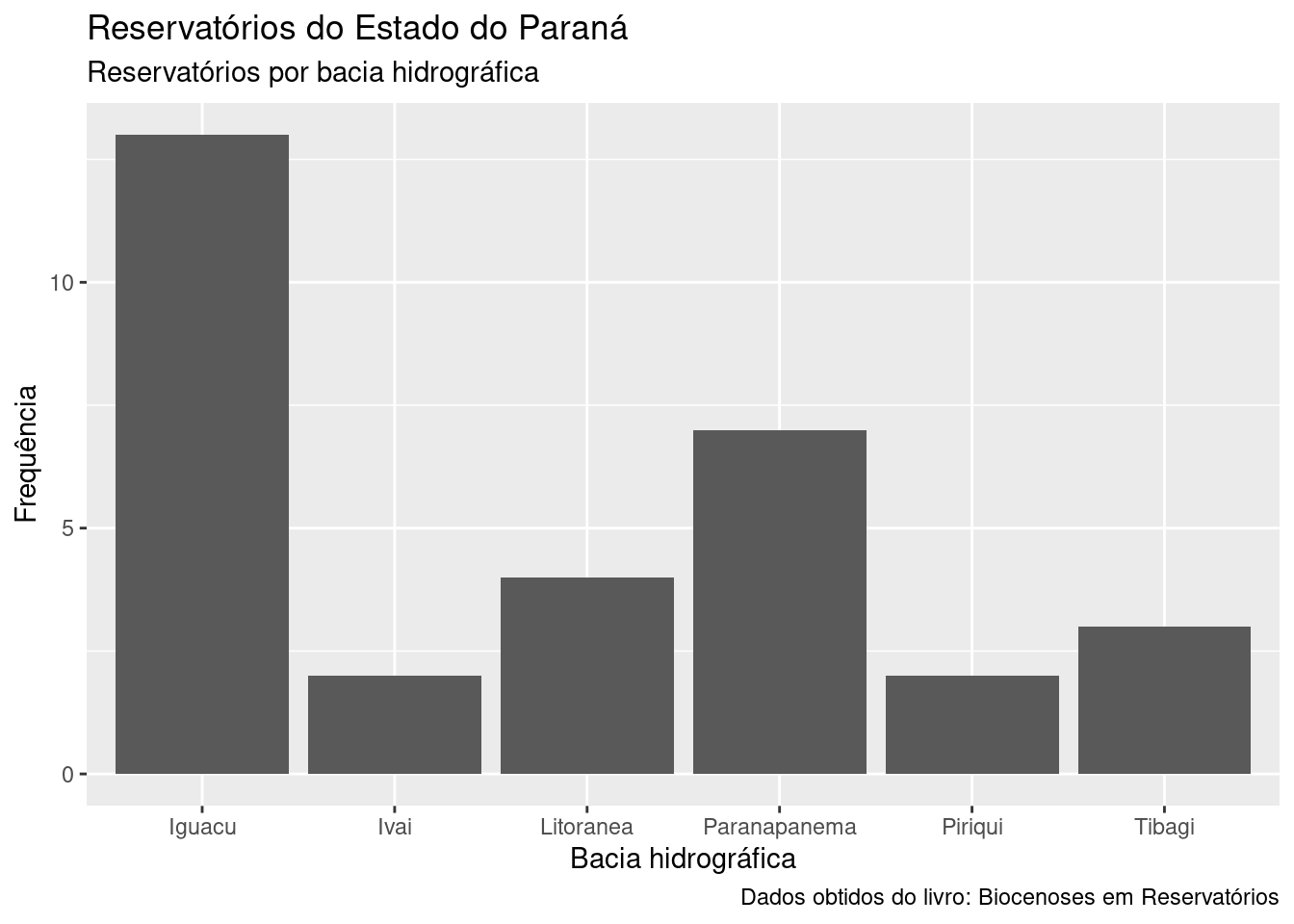

Gráfico de frequência relativa

Utilizando o ggplot2 é simples construir um gráfico de frequência relativa.

ggplot(res, aes(x = Bacia, y = ..prop.., group = 1)) +
  geom_bar()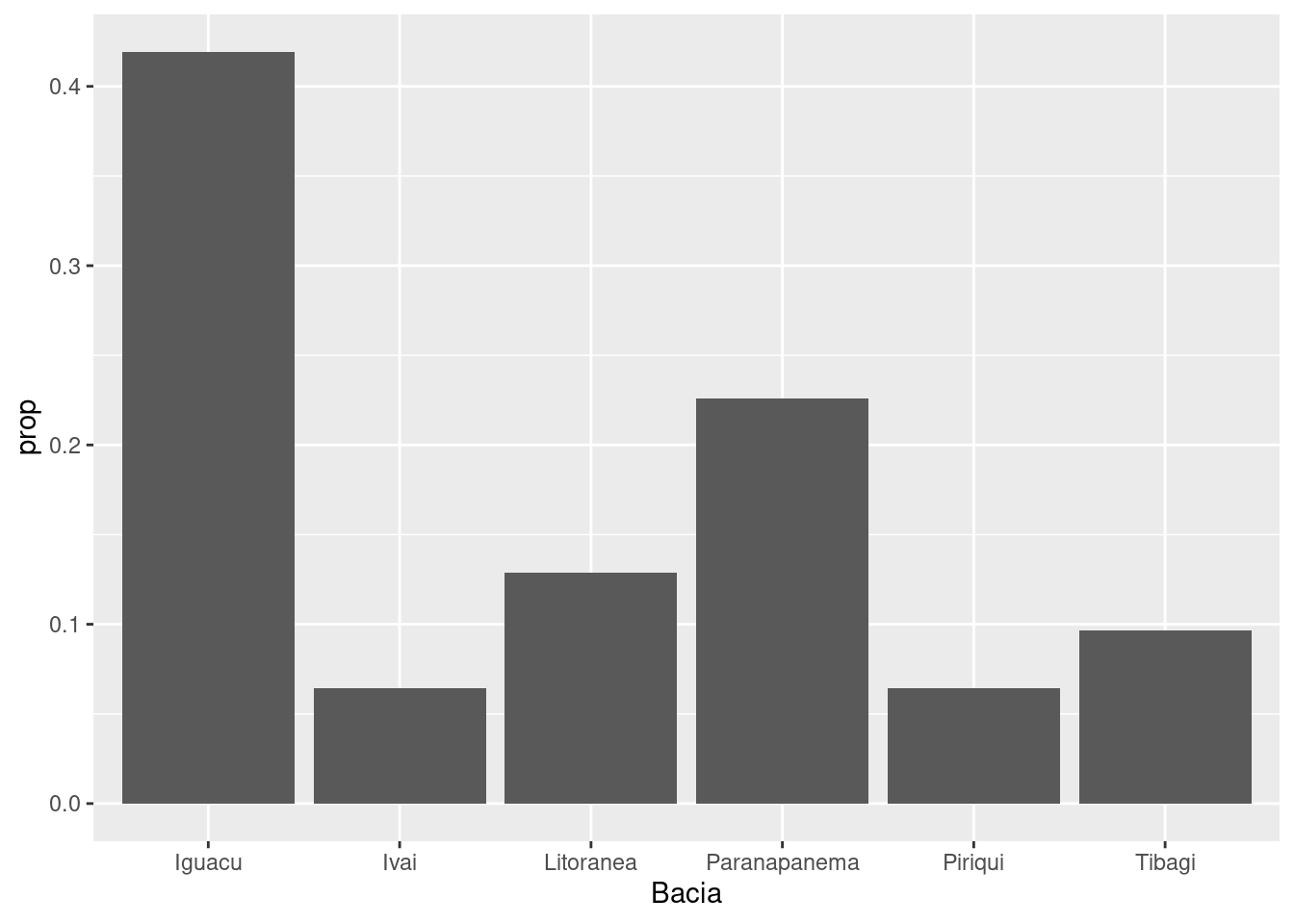

Veja que para isto transformou as contagens em proporções. Se quisermos transformar em percentuais então:

ggplot(res, aes(x = Bacia, y = ..prop.., group = 1)) +
  geom_bar() +
  scale_y_continuous(labels = scales::percent)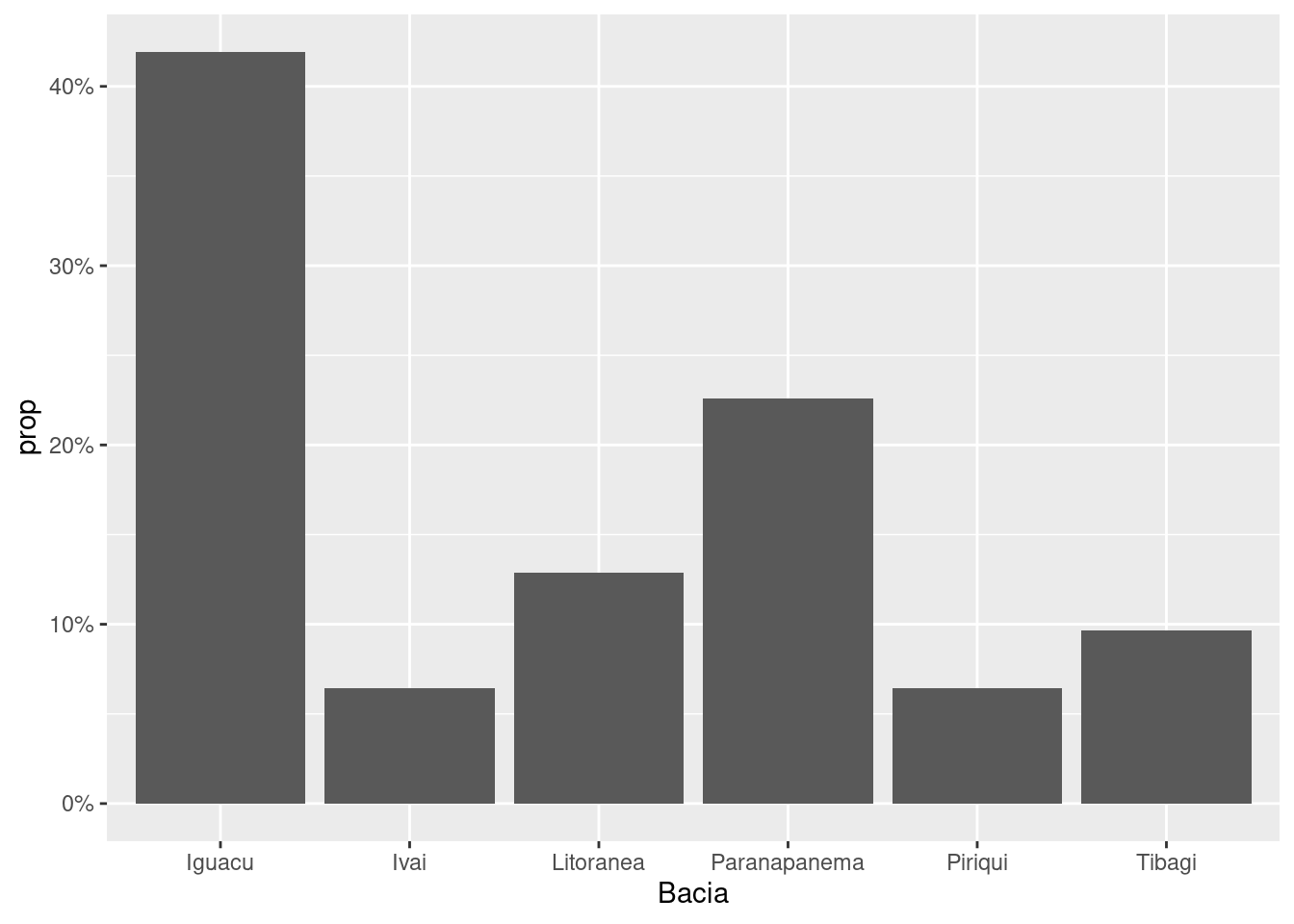

---

Outras opções para construir um gráfico de barras

As figuras que acabamos de fazer apresentam, do modo gráfico, as mesmas informações das tabelas de frequência vistas no início do capítulo sem que fosse necessário contruir a tabela de frequencia, pois o comando geom_bar() já realiza esta contagem.

Entretanto, caso já tivéssemos a tabela de frequência também poderíamos utilizá-la diretamente. No início do capítulo, contruímos a tabela fbacia_rel onde tínhamos 3 colunas: Bacia, Frequencia, Freq_relativa.

Podemos construir gráficos de barras das tabelas Frequencia ou Freq_relativa da seguinte forma:

ggplot(fbacia_rel, aes(x = Bacia, y = Frequencia)) +
  geom_bar(stat = 'identity')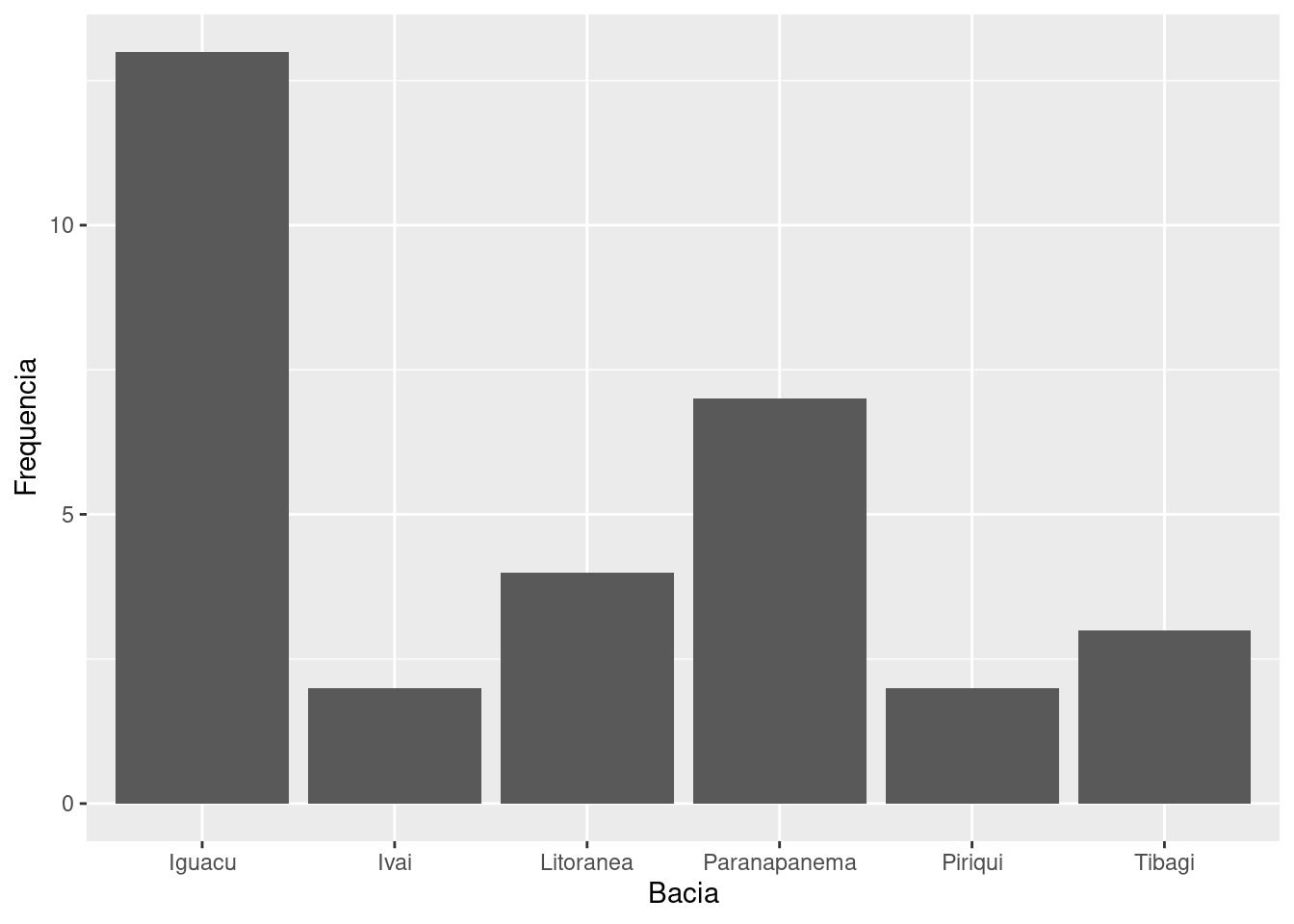

e

ggplot(fbacia_rel, aes(x = Bacia, y = Freq_relativa)) +
  geom_bar(stat = 'identity')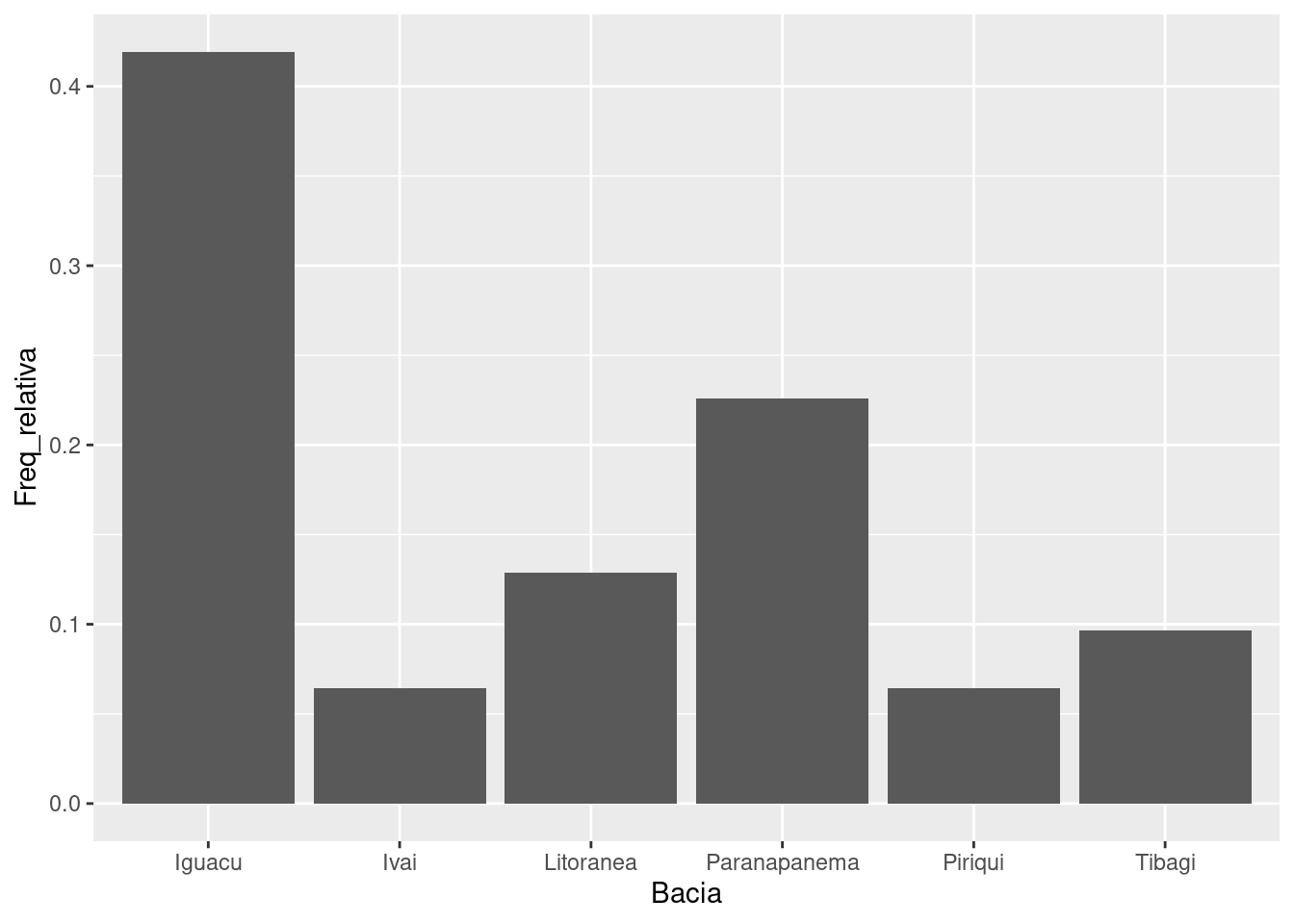

Para utilizar diretamente uma tabela de frequências, devemos oferecer a variável do eixo \(x\), do eixo \(y\) e no comando geom_bar() adicionar o argumento stat = 'identity'. Feito isso, o comando utiliza diretamente os números disponíveis em cada linha da coluna Frequencia.

---

Gráfico de frequência para variáveis categóricas ordenadas

Para variáveis categóricas ordenadas valem os mesmos comandos apresentados acima. Usamos a função geom_bar() para construir os gráficos de barras. A diferença é que antes da construção, é necessário que a variável em questão tenha sido transformada para um fator ordenado.

Lembrando o que fizemos no início do capítulo, esta transformação pode ser feita para a variável Trofia com os comandos:

res = res %>% 
  mutate(Trofia = factor(Trofia, ordered = TRUE, 
                         levels = c('Oligotrófico', 'Mesotrófico', 'Eutrófico')))

Feito isto, o comando geom_bar() vai organizar os níveis de acordo com a sequência definida:

ggplot(res, aes(x = Trofia)) +
  geom_bar()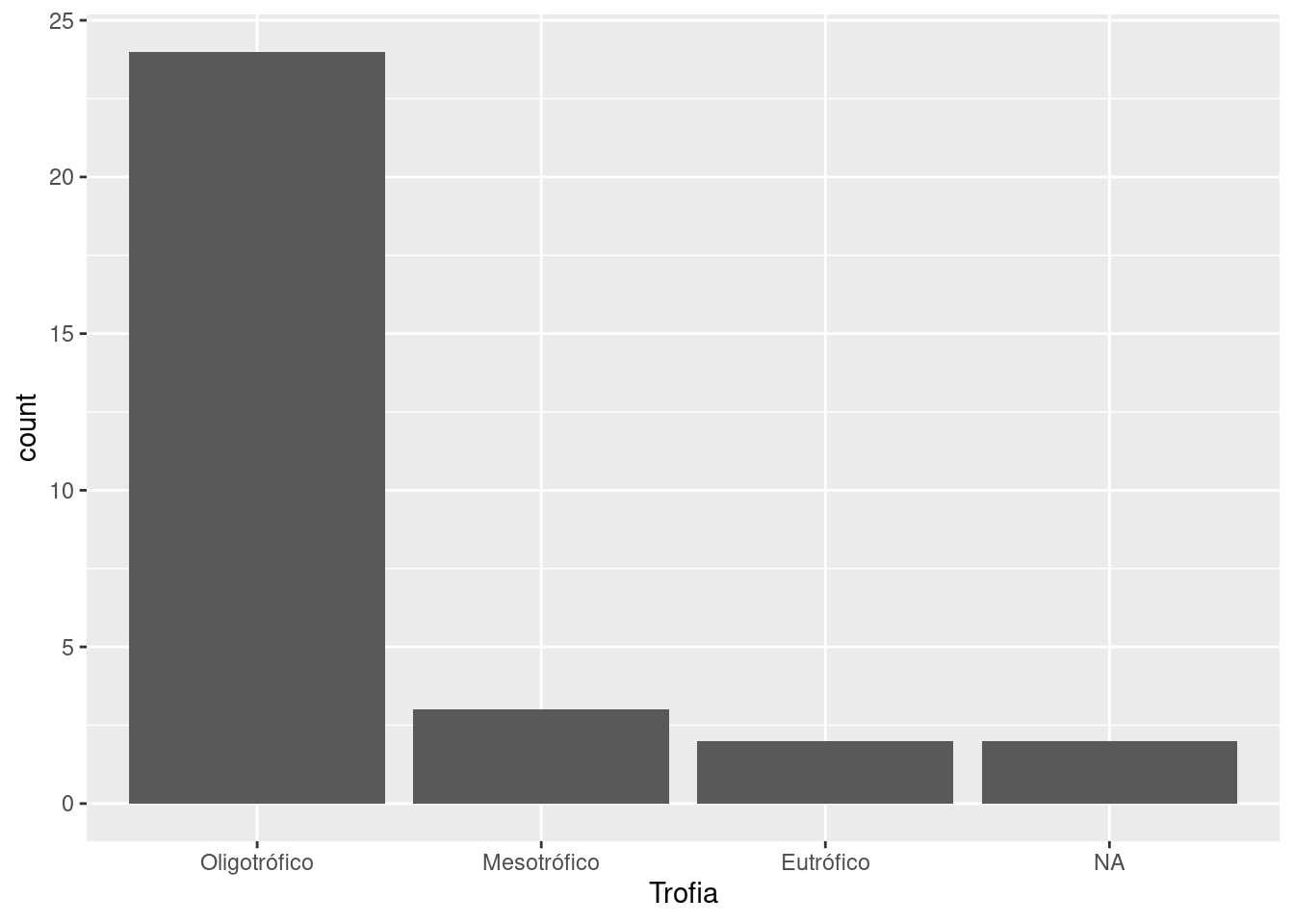

E caso seja necessário retirar reservatórios com dados faltantes em Trofia, podemos fazer:

res %>% 
  drop_na(Trofia) %>% 
ggplot(aes(x = Trofia)) +
  geom_bar()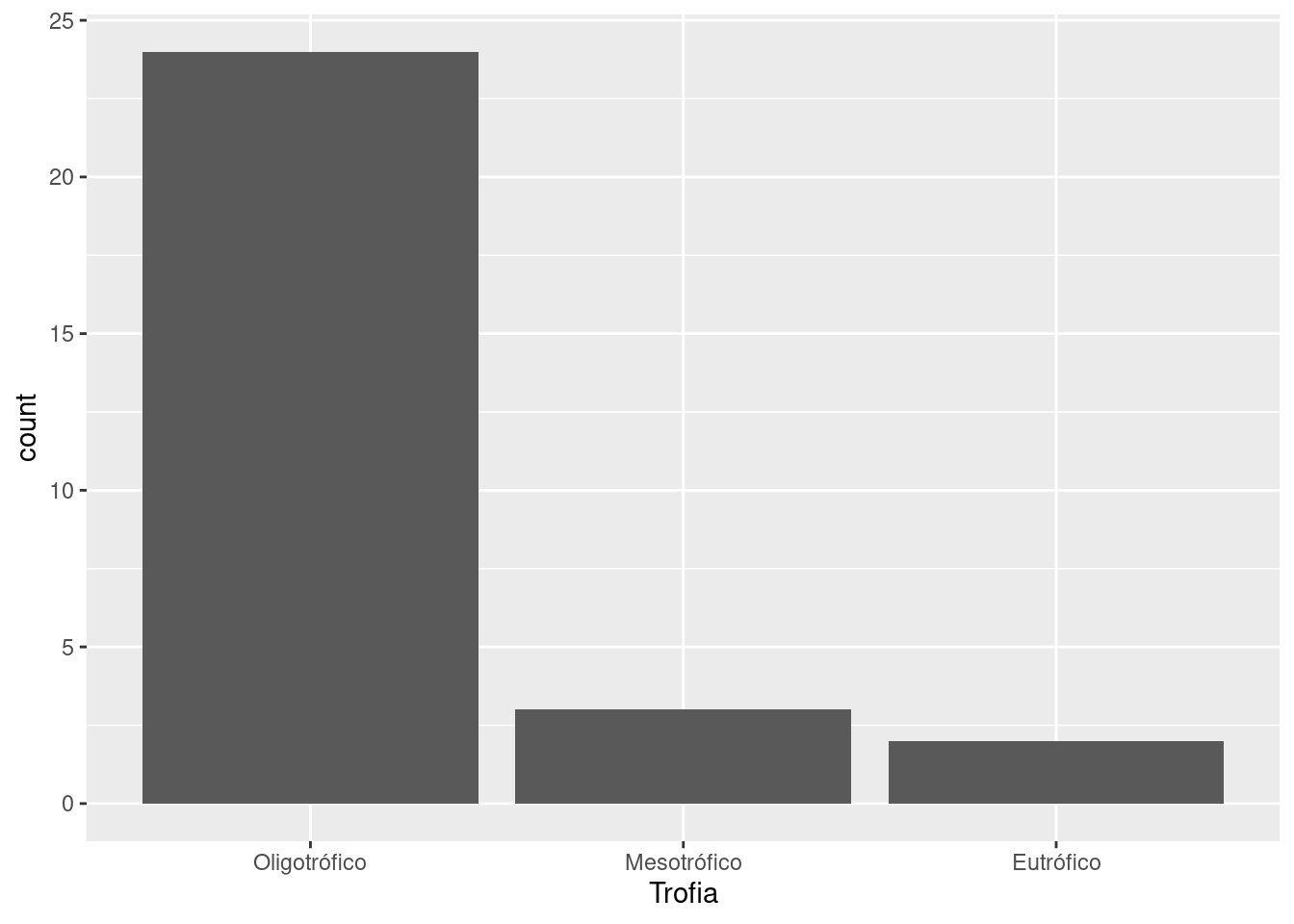

No comando acima, a tabela de dados não entra dentro do comando ggplot(), ela é inicialmente processada e usamos o operador %>% para inserir o resultado do processamento no comnado gráfico. Esta é outra maneira de combinar capacidade de processamento de dados e apresentação gráfica com o conjunto de pacotes em tidyverse.