Capítulo 18 Teste t de Student

De acordo com o que discutimos no capítulo 16, o modelo normal de probabilidades não é a melhor aproximação para a distribuição das madias amostrais quando não conhecemos $\mu$ e $\sigma$ e/ou quando o tamanho amostral $n$ é pequeno. Nesta situação, apresentamos a distribuição t de Student como uma opção mais apropriada para o cálculo de um intervalo de confiança. Da mesma forma, o teste $Z$ que introduzimos no capítulo 17 assume que a distribuição das médias amostrais é normalmente distribuída e que a variância populacional $\sigma$ seja conhecida, uma informação que não temos na prática científica.

Seguindo este raciocínio portanto, iremos apresentar o teste t para verificar uma hipótese sobre uma média populacional. Este teste é utilizado em substituição ao teste $Z$ quando $\sigma$ é desconhecido e/ou o tamanho amostral é pequeno. O teste segue também a mesma lógica discutida no teste $Z$, porém estabelece que a distribuição das médias amostrais é melhor descrita pela distribuição $t$ e não pela distribuição normal.

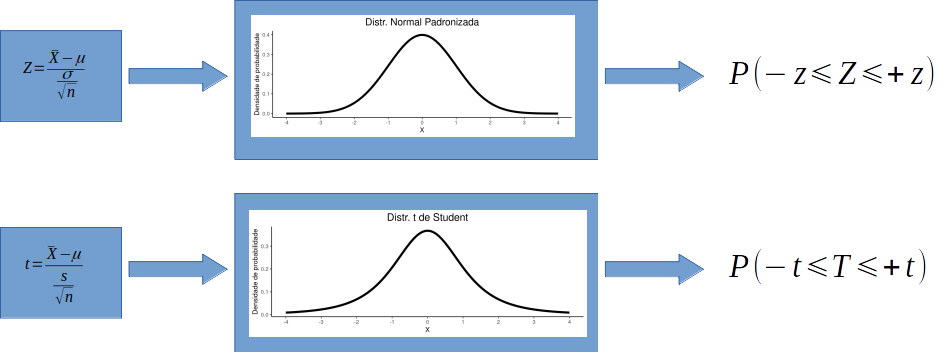
Figure 18.1: Teste Z versus teste t. Estatística do teste e distribuição de probabilidades

18.1 Teste t para uma média populacional

Considere um exemplo simples. Dados do Banco Central do Brasil dizem que moedas de $R\$ 0,10$ da segunda geração pesam 4.8 gramas. Você tem $8$ moedas no bolso e resolve testar essa afirmação pesando cada moeda. Os pesos obtidos são: $X = 5.1, 5, 4.8, 5, 5, 4.9, 4.9, 4.7$.

Inicialmente, devemos estabelecer nossa hipótese nula ($H_0$), nossa hipótese alternativa ($H_a$) e o nível se significância $\alpha$. Iremos estabelecer $\alpha = 0,05$ e as hipóteses como:

$H_0: \mu = 4.8$ gramas

$H_a: \mu \ne 4.8$ gramas

Como não conhecemos $\sigma$ e temos uma amostra pequena, a posição das médias amostrais seguirá uma distribuição $t$ de Student e a estatística do teste será:

\[t = \frac{\overline{X} - \mu}{s_{\overline{X}}}\]

sendo o erro padrão amostral obtido por:

\[s_{\overline{X}} = \frac{s}{\sqrt{n}}\]

O cálculo de $t$ é muito similar ao escore $Z$. No entanto, substituímos $\sigma$ por $s$. Como visto no capítulo 16, as distribuições de $t$ e de $Z$ são muito similares. Entretanto, para amostras pequenas e quando $\sigma$ é desconhecido, a curva de $t$ nos fornece uma melhor estimativa das probabilidades associadas a distribuição das médias amostrais.

Para este exemplo, temos uma amostra de tamanho $n = 8$ com média $\overline{X} = 4.925$g e desvio padrão $s = 0.13$g. O valor de $t$ pode ser calculado por:

\[t_{c} = \frac{\overline{X} - \mu}{s_{\overline{X}}} = \frac{\overline{X} - \mu}{\frac{s}{\sqrt{n}}} = \frac{4.925 - 4.8}{\frac{0.13}{\sqrt{8}}} = 2.76\]

Assim como fizemos para a distribuição $Z$, devemos encontrar a probabilidade de obtermos um valor tão ou maior que o módulo de $t_c$. Na figura abaixo, nosso resultado fica:

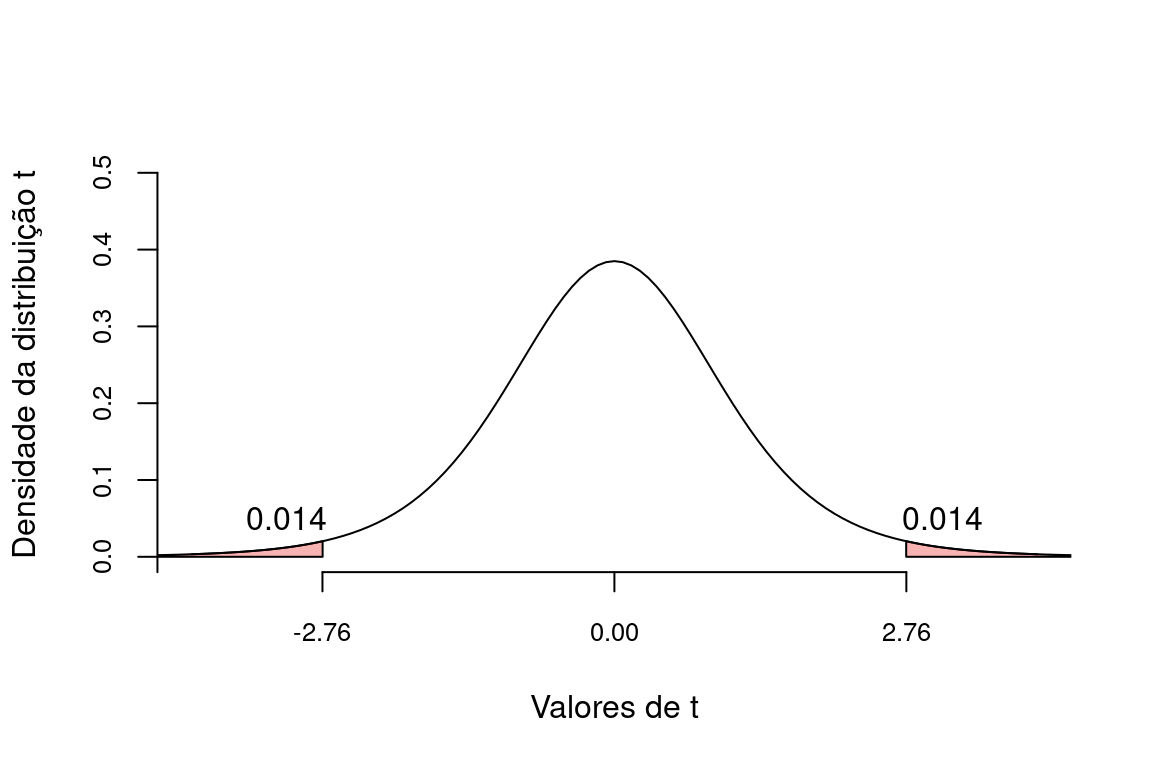
A probabilidade de encontrarmos um valor de $t_c$ tão ou mais extremo segundo a hipótese nula foi de $p = 0.028$. Uma vez que este valor é menor que o nível crítico $\alpha = 0,05$, concluímos que existe evidência suficiente para rejeitar $H_0$ e aceitar a hipótese alternativa de que as moedas de $10$ centavos não provém de uma população estatística com $\mu = 4,8$ gramas. Nossa conclusão é portanto, que as moedas de $R\$ 0,10$ são mais pesadas que $4,8$ gramas.

No R, o teste $t$ discutido acima pode ser realizado por:

t.test(X, mu = 4.8)

## 
##  One Sample t-test
## 
## data:  X
## t = 2.7584, df = 7, p-value = 0.02816
## alternative hypothesis: true mean is not equal to 4.8
## 95 percent confidence interval:
##  4.817844 5.032156
## sample estimates:
## mean of x 
##     4.925

Nos comandos acima, $X$ é a amostra e o argumento mu representa a expectativa sobre a média populacional segundo $H_0$. Como resultados temos:

a indicação de que fizemos um teste $t$ para uma amostra: One Sample t-test;
o valor de $t$ calculado: t = 2.7584;
os graus de liberdade: df = 8 - 1 = 7; e
o valor de p = 0.028.

Podemos ver ainda o valor da média amostral ($\overline{X} = 4.925$) e o intervalo de confiança a $95\%$ (4.817844 - 5.032156).

18.2 Graus de liberdade

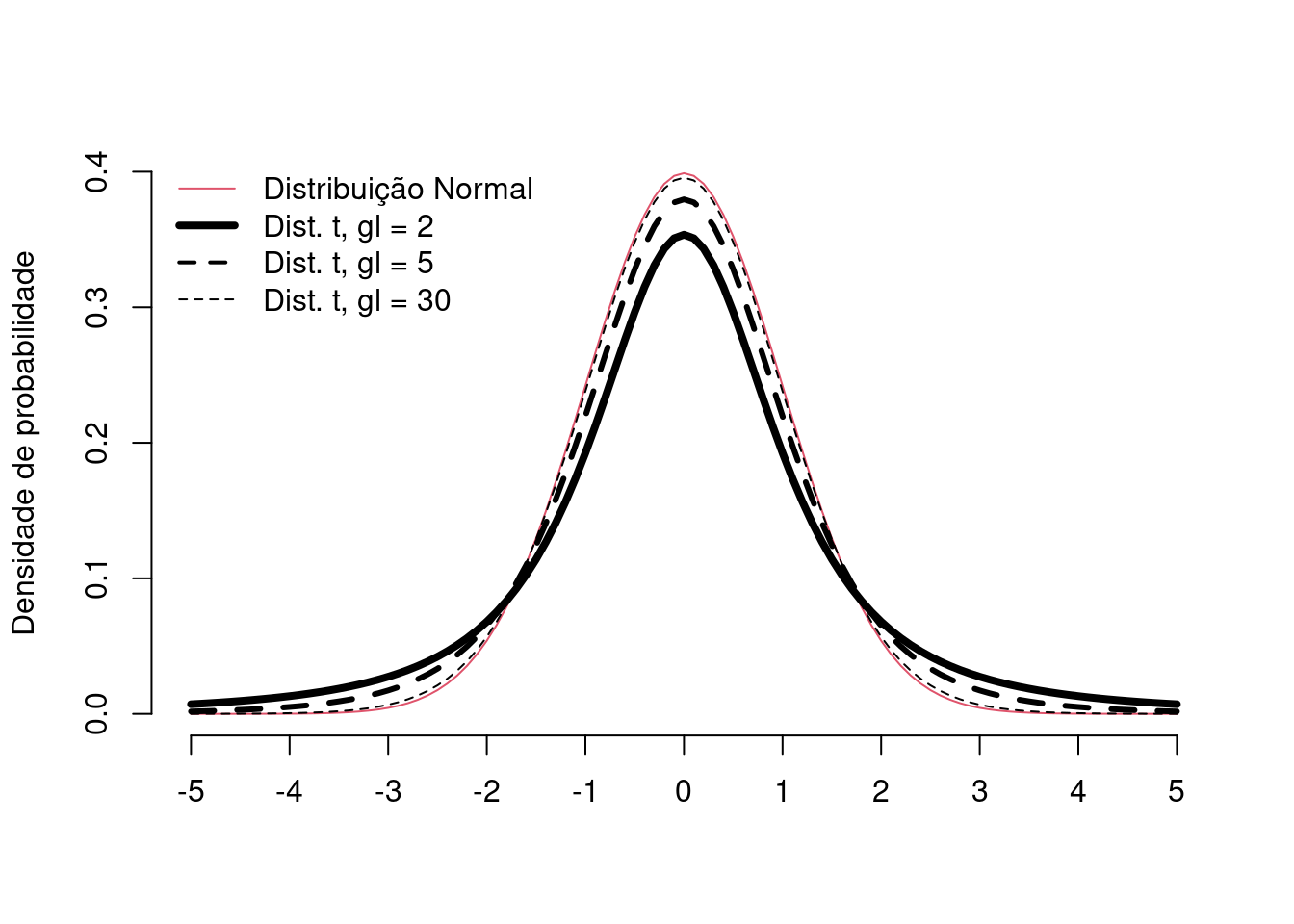
A distribuição $t$ como várias outras distribuições amostrais utilizadas em inferência estatística, muda seu formato em função do que chamamos de graus de liberdade ($gl$). Os graus de liberdade têm relação com o tamanho amostral. No caso do teste $t$ para $1$ amostra, esta relação é simplesmente: $gl = n-1$.

À medida que os graus de liberdade aumentam, o formato da distribuição $t$ se assemelha ao formato da distribuição Normal padronizada. De fato, para graus de liberdades altos (ex. $n \ge 30$), os formatos das distribuições $Z$ e $t$ são praticamente indistinguíveis. Na prática, isto faz que as distribuição $Z$ raramente seja utilizada.

18.3 Probabilidades no teste $t$ de Student: a tabela $t$

A rejeição uo aceitação da hipótese nula em um teste $t$ pode ser feita por meio da obtenção do valor de p ou pela comparação do $t$ calculado com valores críticos de referência para determinado nível de significância. O primeiro caso foi o que apresentamos acima e depende de um software estatístico para obtermos valores exatos de $p$. O segundo caso, pode ser feito com auxílio da Tabela $t$, em que limites críticos de $t$ são disponibilizados para diferentes níveis de significância e graus de liberdade.

Atualmente, o uso da tabela $t$ têm finalidade em grande parte didática e, por este motivo, vamos apresentá-lo aqui rapidamente. No entanto, fora da sala de aula, o teste $t$ será invariavelmente conduzido por meio de um software estatístico este método que permitirá a obtenção do valor exato de $p$.

Na tabela $t$ (acesse aqui), a primeira coluna mostra os graus de liberdade de $1$ a $120$. O cabeçalho da tabela de $90\%$ a $0,1\%$ mostra a área na distribuição de $t$ nas caldas inferior e superior.

Vamos retornar ao exemplo da moedas de $R\$0,10$ para exemplificar sua utilização. Neste exemplo a tinhamos $8$ ($gl = 7$ graus de liberdade) e o teste foi feito com $\alpha =0,05$. Se buscarmos na linha $gl = 7$ e a coluna $5\%$ ($\alpha = 0,05$), encontraremos o valor $t = 2,3646$. Este é o chamado $t$ crítico ($t_{crítico}$). Acima deste valor e abaixo de sua contraparte negativa temos exatamente $5\%$ da área na disribuição $t$. Deste modo, qualquer valor calulado maior que $t_{crítico}$ estará mais para a extremidade da distribuição e consequentemente estará associado a menores valores de probabilidade. Neste sentido:

$t_{calculado} \ge t_{crítico}$ leva a rejeição de $H_0$
$t_{calculado} < t_{crítico}$ leva a aceitação de $H_0$

O resultado do teste estatístico em nosso exemplo foi $t_c = 2.76$ que é maior que $2,3646$. Isto nos leva à mesma decisão anterior (rejeitar $H_0$), ainda que por meio da tabela $t$ não tenhamos o valor exato de probabilidade.

18.4 Teste t para comparação de duas médias independentes

O que vimos no teste $t$ para uma amostra pode ser facilmente extendido para testarmos a diferenças entre duas amostras.

Os dados abaixo mostram o tempo de coagulação sanguínea (em minutos) em ratos machos adultos tratados com dois tipos de drogas, retirado do livro Biostatistical Analysis (Zar 2010), pp. 130-134.

Droga	Tempo
Droga A	8.8
Droga A	8.4
Droga A	7.9
Droga A	8.7
Droga A	9.1
Droga A	9.6
Droga B	9.9
Droga B	9.0
Droga B	11.1
Droga B	9.6
Droga B	8.7
Droga B	10.4
Droga B	9.5

Nosso objetivo é testar se as duas drogas resultam, em média, no mesmo tempo de coagulação. Inicialmente, vamos fazer um gráfico de dispersão para verificar a distribuição do tempo de coagulação para cada droga.

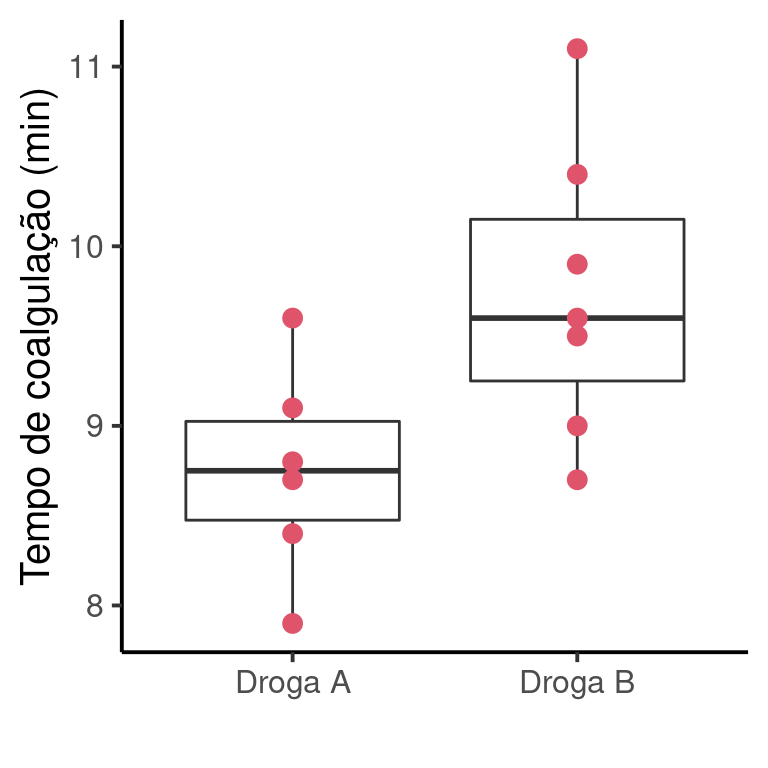
As médias, desvios padrões e tamanhos amostrais de cada grupo são:

Droga	Tempo médio	Desvio	n
Droga A	8.75	0.58	6
Droga B	9.74	0.82	7

Para testarmos se as médias dos grupos provém de populações estatísticas com diferentes $\mu's$ devemos estabelecer nosso nível de significância (por exemplo $\alpha = 0.05$) as hipoteses estatísticas:

$H_0: \mu_A = \mu_B$ gramas

$H_a: \mu_A \ne \mu_B$ gramas

O teste t para duas amostras é calculado por:

\[t = \frac{(\overline{X_A} - \mu_A) - (\overline{X_B} - \mu_B)}{s_{\overline{X_A}-\overline{X_B}}}\]

Assumindo a hipotese nula em que $\mu_A = \mu_B$ a expressão fica

\[t = \frac{\overline{X_A} - \overline{X_B}}{s_{\overline{X_A}-\overline{X_B}}}\]

em que a quantia $s_{\overline{X_A}-\overline{X_B}}$ é calculada por:

\[s_{\overline{X_A}-\overline{X_B}} = \sqrt{\frac{s^2_{p}}{n_1} + \frac{s^2_{p}}{n_2}}\]

$s_p$ é denominada de variância conjunta calculada por

\[s^2_p = \frac{(n_1 - 1) \times s^2_1 + (n_2 - 1) \times s^2_2}{(n_1 - 1) + (n_2 - 1)}\]

Para este exemplo,

$s_p = 0.52$

$s_{\overline{X_A}-\overline{X_B}} = 0.4$

O valor de t calculado é:

$t_c = -2.476$

Na distribuição t, a probabilidade de encontrar valores tão ou mais extremos que 2.476 é de $p = 0.031$.

Portanto:

$P(|t| \ge 2.476) \le 0.05$

Uma vez que a probabilidade associada ao valor de $t$ é menor que o nível de significância, rejeitamos $H_0$ e assumimos que os tempos médios de coagulação são diferentes. Ao avaliar as média amostrais $\overline{X}_A$ e $\overline{X}_B$, concluímos que a droga $A$ resulta, em média, em tempos menores de coagulação.

References

Zar, Jerrold H. 2010. “Biostatistical Analysis Pearson Prentice-Hall.” Upper Saddle River, NJ.

Estatística nas Ciências Ambientais

Capítulo 18 Teste t de Student

18.1 Teste t para uma média populacional

18.2 Graus de liberdade

18.3 Probabilidades no teste \(t\) de Student: a tabela \(t\)

18.4 Teste t para comparação de duas médias independentes

References