Capítulo 26 O espaço de possibilidades de um experimento
O peixe acará, Geophagus brasiliensis é uma espécie de peixe comumente encontrada em rios e riachos de mata atlântica no siudeste do Brasil. Uma das táticas de forrageamento e alimentação recentemente descrita para a espécie é chamada de virar para pegar (Souza, Sabino, and Garrone-Neto 2019) que envolve virar objetos presentes no substrato (folhas, galhos e cascas de árvores) para encontrar e capturar macroinvertebrados ocultos sob estes objetos. Veja o vídeo.
Ao realizar o ato de virar uma estrutura o indivíduo não sabe se irá encontrar e capturar um alimento. Em probabilidade, podemos chamar esta ação de um experimento aleatório. Um experimento aleatório é aquele que produz um resultado que iremos conhecer somente após sua realização. No entanto, ainda que não saibamos o resultado que uma realização específica do experimento, sabemos quais são os possíveis resultados. Neste exemplo vamos assumir que existem unicamente dois resultados possíveis para o ato de virar para pegar:
\(\{(captura), (não-captura)\}\)
Denominamos de evento, cada um destes resultados pssíveis e, ao conjunto de todas as possibilidades denominamos de espaço amostral do experimento aleatório. Geralmente utilizamos o símbolo \(\Omega\) para nos referir ao espaço amostral. Neste caso:
\(\Omega = \{(captura), (não-captura)\}\)
Experimento aleatório: aquele que possui resultados possíveis mas que são observados somente APÓS a realização do experimento.
Espaco amostral: conjunto de TODAS as possibilidades de um experimento aleatório.
Evento: cada resultado de um experimento aleatório.
26.1 Probabilidades de um evento
Embora não saibamos qual será o resultado de um experimento particular, podemos nos perguntar sobre qual a chance de ocorrência de cada evento, neste caso, qual a chance de um alimento ser capturado. Em probabilidade perguntamos sobre qual a probabilidade de captura \(P(captura)\). Uma probabilidade \(P(captura) = 0\) significa que o animal jamais irá capturar um alimento ao virar um objeto. Por outro lado, \(P(captura) = 1\) significa que irá capturar um alimento sempre que virar um objeto. No mundo real, a probabilidade será alguma coisa entre estes dois extremos, ou seja, \(0 \le P(captura) \le 1\).
Como podemos estimar esta probabilidade?
A resposta é: observando! ou experimentando!
Delineamos um estudo em que um observador irá encontar um animal e seguí-lo, contando o número de objetos virados (\(\#viradas\)) e o número de capturas (\(\#capturas\)). Digamos que em um dia de observação o animal vire 10 objetos e capture 4 itens. Nossa estimativa da probabilidade de captura será:
\[P(captura) = \frac{\#capturas}{\#viradas} = \frac{4}{10} = 0.4\]
Naturalmente, como os dois únicos eventos do espaço amostral são \((captura)\) e \((não-captura)\), a probabilidade de não-captura é:
\[P(não-captura) = \frac{\#não-capturas}{\#viradas} = \frac{6}{10} = 0.6\]
e como estes eventos, além de serem únicos no espeço amostral são também mutuamente exclusivos, temos que:
\[P(captura) + P(não-captura) = 1 = P(\Omega)\] Por evento mutuamente exclusivos entendemos que ambos não podem ocorrer ao mesmo tempo, ou seja, a ocorrência de um exclui a possibilidade da ocorrência do outro.
A probabilidade de \((não-captura)\) é conhecida como o complemento da probabilidade de \((captura)\). Utilizando uma notação comum à operações com conjuntos, também poderíamos escrevê-la como:
\[P(não-captura) = P(\overline{captura})\]
26.1.1 Estimando as probabilidades de um evento por amostragem
O valor acima descreve o resultado para a observação de um único indivíduo em um único dia. No entanto, esperamos que existam dias melhores e dias piores para os peixes e uma série de fatotres pode interferir nestes resultados. Por exemplo, como Geophagus brasiliensis é uma espécie visualmente orientada, poderíamos supor que em dias de água turva (como após uma chuva intensa) um indivíduo tenha menor sucesso de captura. Poderíamos supor ainda que o sucesso de captura pode depender da habilidade individual, tamanho do predador, do tamanho da presa, de locais com maior densidade de presas, ou de predadores, etc. Todas esta possíveis causas, além do simples acaso, podeam fazer o número relativos de capturas varie dia-a-dia. Para estimarmos a chance de captura devemos portanto repetir este experimento.
Suponha então que o experimento seja repetido em 30 dias diferentes de observação e que os resultados fossem:
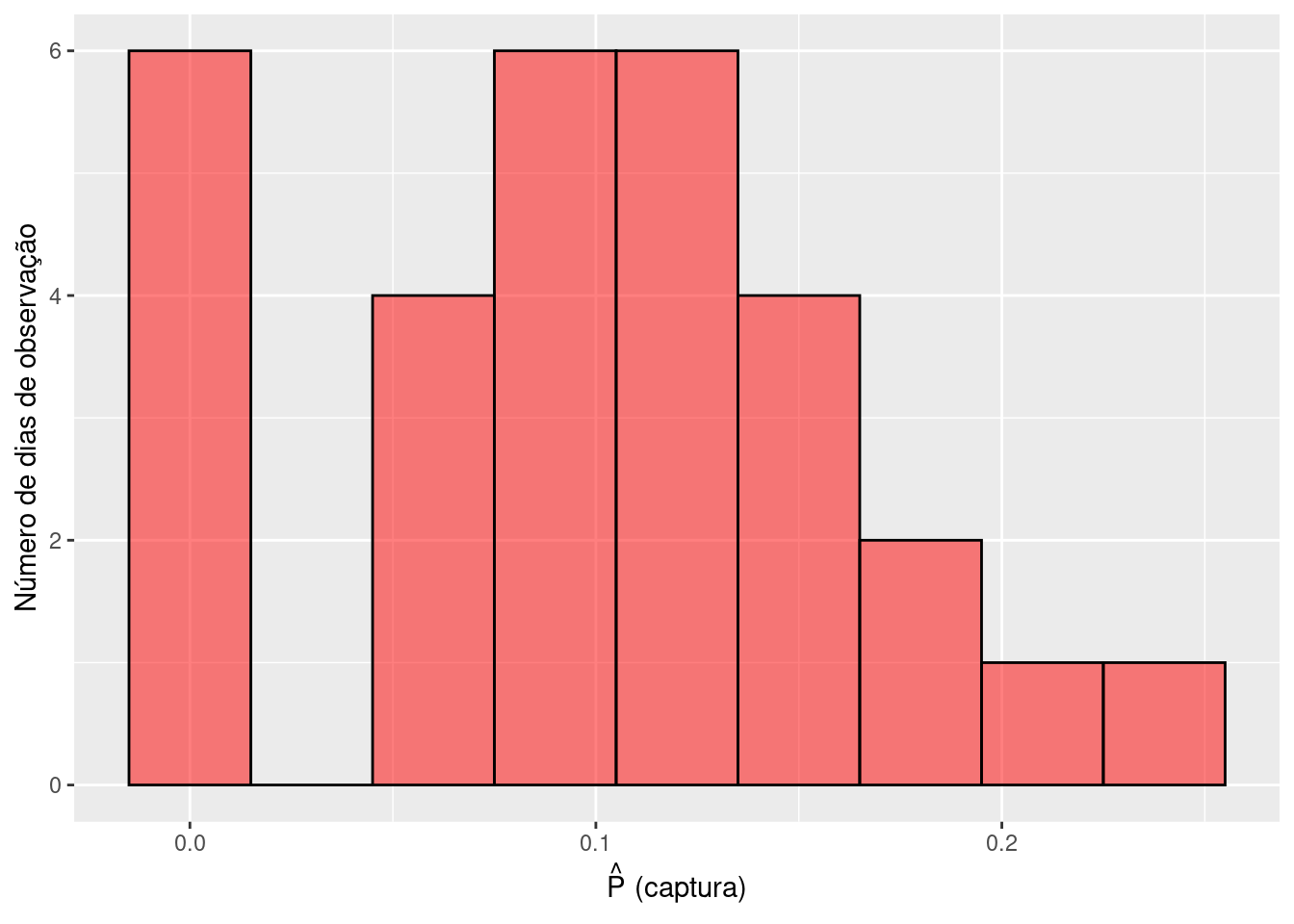
Com base nestes resultados temos estimativas que variam entre 0 e 0.23. Veja que em 6 dias não foi observada nenhuma captura, \(\hat{P}(captura) = 0\). Isto não significa que a captura seja impossível, mas que neste dia em particular, o sucesso foi muito baixo. Tivemos também dias com elevada captura, por exemplo \(\hat{P}(captura) = 0.23\). Isto não significa que o sucesso é sempre desta forma. Na realidade tamanho sucesso parece ser improvável.
Diante destes resultados, poderíamos estimar que em média a probabilidade de captura esteja em \(\overline{P}(captura) = 0.09\)
A estimativa de \(\overline{P}(captura) = 0.09\) resulta de um número finito de repetições do experimento, é portanto uma estimativa da verdadeira probabilidade de captura. Lembre-se que:
Ao jogar uma moeda para o alto exatamente 10 vezes, provavelmente não teremos exatamente 5 caras e 5 coroas. Esta proporção esperada pode ser somente aproximada à medida que aumentemos indefinidamente o número de jogadas.
O mesmo vale para o experimento de captura que descrevemos acima. O valor exato de \(P(captura)\) só será observado após infinitas observações deste experimento.
Obs.: Note que inseri o símbolo \((\hat{})\) para identificar que esta probabilidade não se refere ào valor verdadeiro, mas a uma estimativa deste valor, obtiva por meio de amostragem. Da mesma forma, o símbolo \((\overline{})\) identifica o valor da média amostral dos resultados obtidos após a realização dos 30 do experimento. Aqui valem os conceitos de população estatística e amostra (Capítulo ??). O valor verdadeiro da probabilidade de captura é o valor esperado na população estatística deste tipo de experimento, enquanto os valores observados são resultados obtidos a partir de amostras particulares. Nos referimos a cada uma destas amostras como réplicas do experimento. A partir deste conjunto de réplicas, poderíamos calcular uma média aritmética e um intervalo de confiânça para \(P(captura)\), o que seria nossa melhor estimativa para o fenômeno.
Os conceitos de probabilidade são essenciais ao delineamento experimental, pois modelos probabilísticos nos dizem sobre quais são os resultados possíveis deste experimento e sobre quais as chances de observação de cada resultado. Assim, temos uma expectativa sobre o que vamos encontrar no futuro. Após a realização do experimento, utilizamos métodos e técnicas estatísticas para analizar os resultados e tirar concluções sobre a ocorrência destes rsultados a luz de um ou mais modelos probabilísticos. Neste caso, podemos pensar nos modelos probabilísticos como as hipóteses que serão contrastadas com os resultados obtidos após a realização do experimento. Iremos explorar a fundo estas questões nos capítulos ?? a 38.