Capítulo 10 Análise bidimensional: variáveis quantitativas
Neste capítulo iremos medir o grau de associação entre duas variáveis quantitativas denominadas de \(X\) e \(Y\). Para isto falaremos dos conceitos de covariância e correlação. Não estamos interessados em verificar se \(Y\) depende funcionalmente de \(X\) ou vice-versa. Estamos interessados somente em medir a intensidade de associação entre as duas variáveis. Quando calcularmos a covariância entre \(Y\) e \(X\) (\(s_{YX}\)), por exemplo, poderíamos inverter a ordem fazendo \(s_{XY}\) e teríamos exatamente os mesmo resultados. O mesmo vale para o coeficiente de correlação (\(r_{YX} = r_{XY}\)). Dizemos que existe uma simetria entre as variáveis quando calculamos a covariância ou correlação. Esta simetria não vale quando formos abordar o conceito de regressão linear (Capítulo 22), quando assumimos explicitamente que \(Y\) é função de \(X\).
Estamos interessados em diferenciar três situações que podem ser visualizadas nos gráficos de dispersão abaixo:
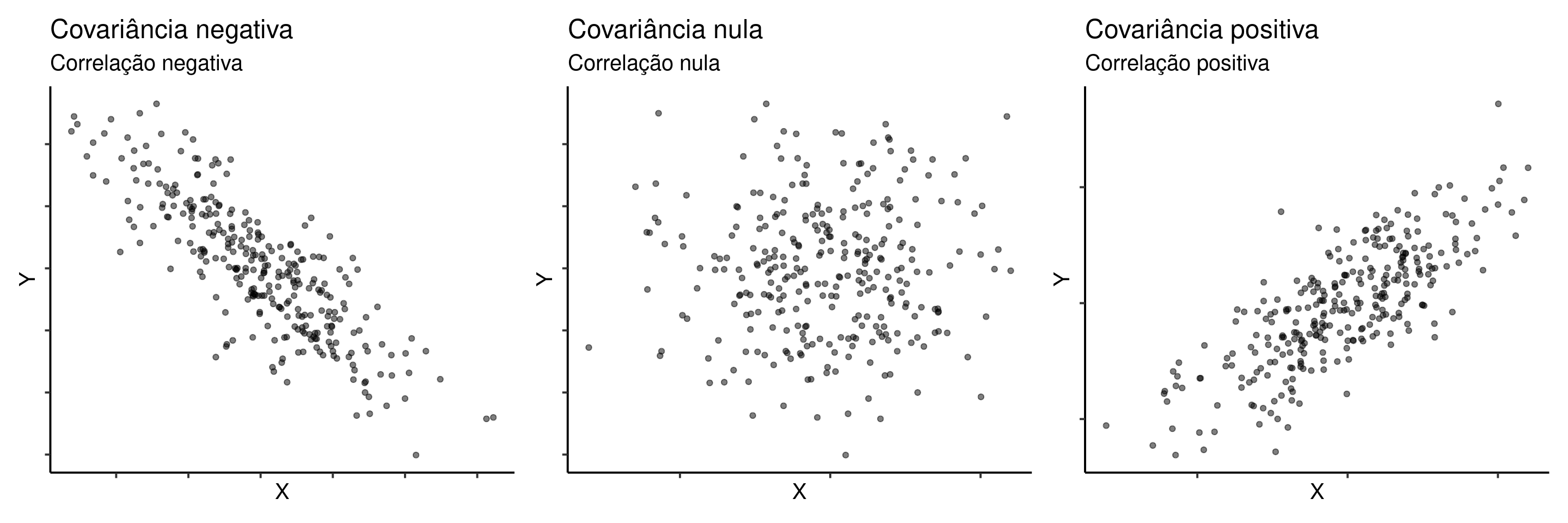
10.1 Covariância entre \(Y\) e \(X\)
Vamos retomar o conceito de variância amostral para em seguida introduzir o conceito de covariância amostral.
A variância amostral de \(Y\) por exemplo, pode ser obtida subtraindo cada observação em \(Y\) de sua média (\(\overline{Y}\)) e elevando esta subtração ao quadrado \((Y_i - \overline{Y})^2\). Ao somar para todos os valores de \(Y_i\) teremos o somatório dos quadrados de \(Y\) (\(SQ_Y\)).
\[SQ_Y = \sum_{i-1}^{n} (Y_i - \overline{Y})^2 = \sum_{i-1}^{n}(Y_i - \overline{Y}) (Y_i - \overline{Y})\]
Dividindo \(SQ_Y\) por \(n-1\) teremos a variância amostral de \(Y\) (\(s^2_Y\)).
\[s^2_Y = \frac{\sum_{i-1}^{n} (Y_i - \overline{Y})^2}{n-1}\]
No capítulo 6 denominamos esta quantia simplesmente por \(s^2\). Aqui vamos usar uma notação diferente (\(s^2_Y\)), pois haverá outros estimadores de variância envolvidos, de modo que deveremos ser mais claros a respeito de qual estimador estaremos nos referindo.
Adotando o mesmo procedimento para \(X\), podemos calcular o somatório dos quadrados de \(X\) (\(SQ_X\)).
\[SQ_X = \sum_{i-1}^{n} (X_i - \overline{X})^2 = \sum_{i-1}^{n}(X_i - \overline{X}) (X_i - \overline{X})\]
e a variância amostral de \(X\) (\(s^2_X\)).
\[s^2_X = \frac{\sum_{i-1}^{n} (X_i - \overline{X})^2}{n-1}\]
Combinando as duas ideias, teremos o produto cruzado de \(Y\) e \(X\) (\(SQ_{YX}\))
\[SQ_{YX} = \sum_{i-1}^{n}(Y_i - \overline{Y}) (X_i - \overline{X})\]
e finalmente a covariância amostral entre \(Y\) e \(X\) (\(s_{YX}\)).
\[s_{YX} = \frac{\sum_{i-1}^{n}(Y_i - \overline{Y}) (X_i - \overline{X})}{n-1}\]
10.2 Coeficiente de correlação linear de Pearson \(r\)
Quando estamos interessados em medir o grau de correlação entre duas variáveis utilizamos o coeficiente de correlação de Pearson (\(r\)). O coeficiente \(r\) mede a intensidade da correlação linear entre \(Y\) e \(X\). Vimos que a covariância amostral (\(s_{YX}\)) mede a intensidade de uma associação linear entre \(Y\) e \(X\). A covariância entretanto, não tem limite superior ou inferior, pois sua magnitude depende da ordem de grandeza das variáveis envolvidas. O coeficiente de correlação \(r\) é calculado como a covariância entre \(Y\) e \(X\) padronizada pelo produto dos desvios padrões de \(Y\) e de \(X\).
\[r = \frac{s_{YX}}{s_Y s_X} = \frac{\frac{\sum{(Y_i - \overline{Y})(X_i - \overline{X})}}{n-1}} {\sqrt{\frac{\sum{(Y_i - \overline{Y})^2}}{n-1}} \times \sqrt{\frac{\sum{(X_i - \overline{X})^2}}{n-1}}}\]
\[r = \frac{\sum{(Y_i - \overline{Y})(X_i - \overline{X})}}{\sqrt{\sum{(Y_i - \overline{Y})^2 \sum{(X_i - \overline{X})^2}}}}\]
Esta padronização garante que o índice pode variar entre \(-1\) (correlação perfeitamente linear e negativa) e \(+1\) (correlação perfeitamente linear e positiva), se aproximando de zero quando não existe correlação.
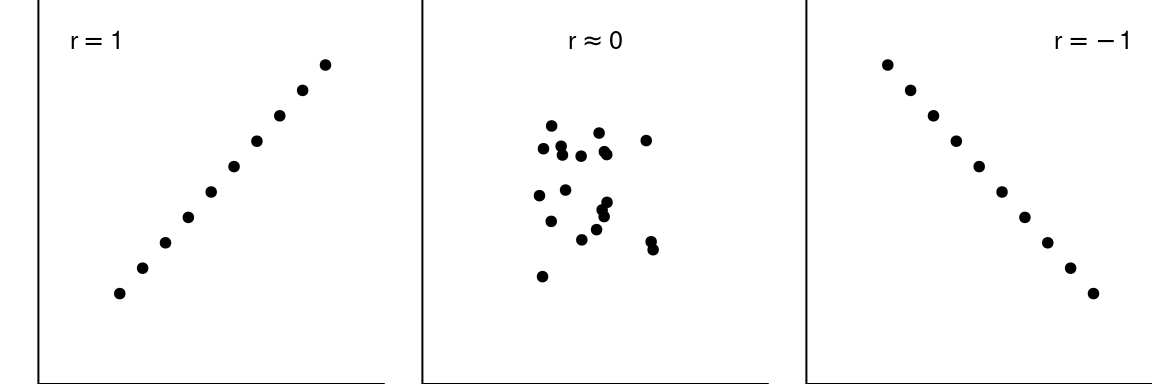
10.3 Exemplo
No conjunto de dados abaixo (Haddon 2010) (disponível em ctigre_haddon.csv) mostra dados da pesca do camarão tigre e do camarão rei entre nos anos de 1976 a 1987. O camarão tigre constitui a espécie alvo da pesca, enquanto o camarão rei aparece como uma espécie acidental.
Importe a base de dados (Disponível em :):
tigre = read_csv("ctigre_haddon.csv")
tigre| Ano | Camarão tigre | Camarão rei |
|---|---|---|
| 1976 | 566 | 10 |
| 1977 | 1437 | 22 |
| 1978 | 1646 | 42 |
| 1979 | 2056 | 33 |
| 1980 | 3171 | 64 |
| 1981 | 2743 | 34 |
| 1982 | 2838 | 59 |
| 1983 | 4434 | 146 |
| 1984 | 4149 | 78 |
| 1985 | 3480 | 75 |
| 1986 | 2375 | 81 |
| 1987 | 3355 | 52 |
c1 = ggplot(tigre, aes(x = Year, y = Tiger)) +
geom_line(color = "red") +
geom_point(color = "red", shape = 19) +
geom_line(mapping = aes(y = King), color = "blue") +
geom_point(mapping = aes(y = King), color = "blue", shape = 19) +
geom_segment(x = 1976, xend = 1976.3, y = 4000, yend = 4000, color = "red") +
geom_segment(x = 1976, xend = 1976.3, y = 3700, yend = 3700, color = "blue") +
geom_text(x = 1976.4, y = 4000, label = "Camarão tigre", hjust = 0) +
geom_text(x = 1976.4, y = 3700, label = "Camarão rei", hjust = 0) +
scale_x_continuous(breaks = tigre$Year) +
theme_classic()
c2 = ggplot(tigre, aes(y = King, x = Tiger)) +
geom_point(shape = 19) +
scale_y_continuous(breaks = seq(0, 150, by = 20)) +
scale_x_continuous(breaks = seq(500, 5000, by = 500)) +
labs(x = "Camarão tigre (Ton)", y = "Camarão rei (Ton)") +
theme_classic()
c1 + c2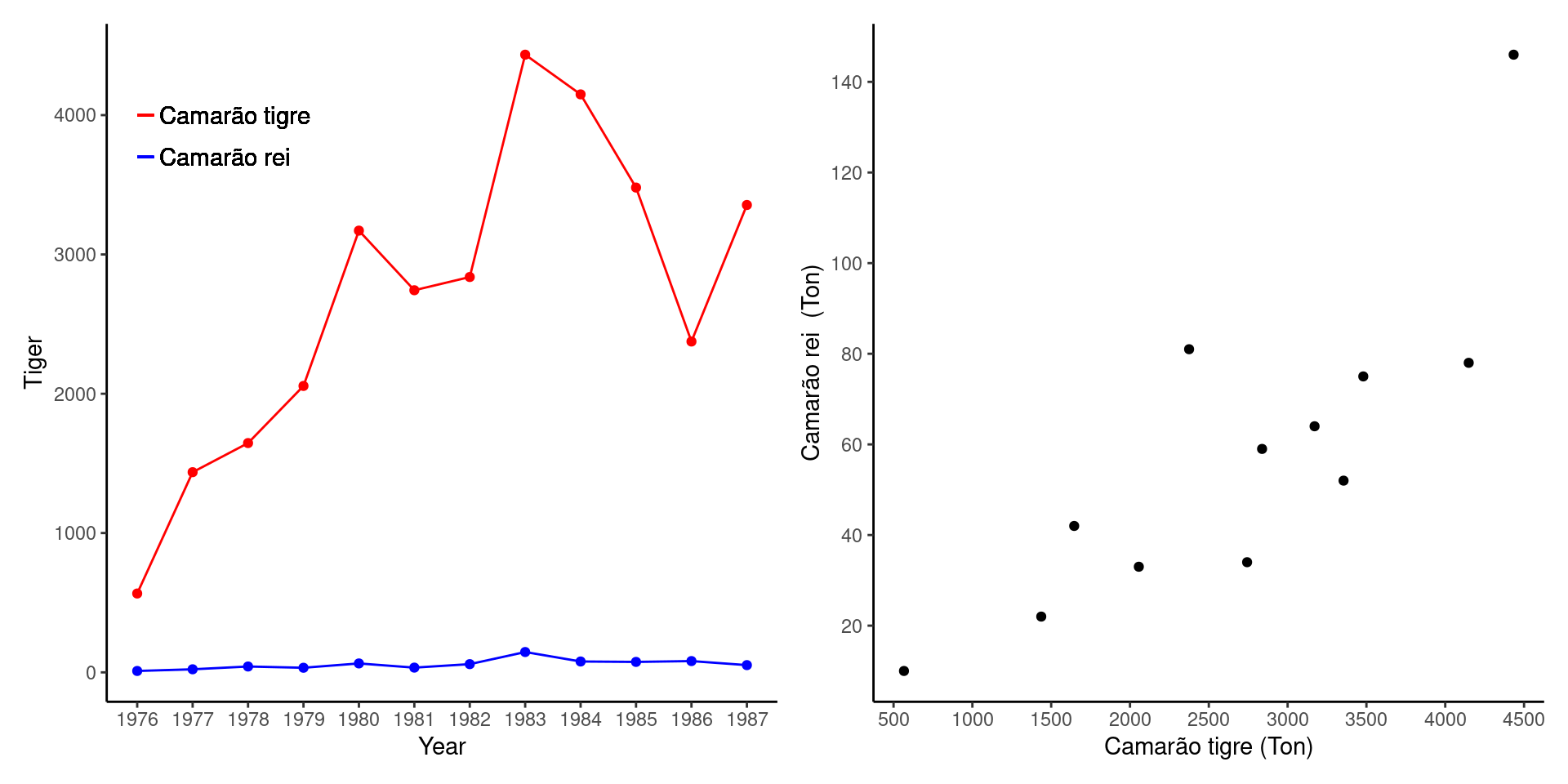
A captura em toneladas do camarão tigre é sempre mais elevada. Entretanto, a figura da direita sugere haver uma associação linear entre as capturas. Nos anos em que houve maiores capturas do camarão tigre parece ter havido também um aumento nas capturas do camarão rei. Dizemos as capturas covariam positivamente. Portanto existe uma correlação positiva entre a captura das duas espécies.
Em nenhum momento estamos dizendo que a captura de uma espécie é a causa do aumento na captura da outra. Muito provavelmente, as abundâncias das duas espécies estão relacionadas a um terceiro fator que gera um comportamento similar na variação das capturas ano a ano. Estamos interessados em mensurar o grau de associação seja pela covariância ou pelo coeficiente de correlação de Pearson.
Em nosso exemplo, a covariância entre as abundâncias dos camarões tigre e rei é positiva (\(s_{tigre-rei} = 3.3293\times 10^{4}\)) e consequentemente a correlação de Pearson também é positiva (\(r = 0.82\)). Confira os cálculos utilizando as expressões apresentadas no capítulo.
No R, a covariância entre \(Y\) e \(X\) pode ser obtida pela função cov:
cov(tigre$Tiger, tigre$King)## [1] 33293E a correlação pela função cor:
cor(tigre$Tiger, tigre$King)## [1] 0.8196913