import pandas as pd # Para manipulação de dados
import matplotlib.pyplot as plt # Para criação e manipulação gráfica
import seaborn as sns # Para criação e manipulação gráfica
import numpy as np # Para operações matemáticas e matriciaisMétodo dos Mínimos Quadrados na Regressão Polinomial
Implementação em Python usando Álgebra Matricial
Tutorial prático para implementar o método dos mínimos quadrados em Python para modelos polinomiais, aplicando os conceitos de álgebra linear e estatística básica.
1 📚 Introdução
DicaObjetivos
Neste tutorial, vamos implementar o Método dos Mínimos Quadrados (MMQ) em Python para ajustar um modelo de regressão polinomial de segundo grau.
Objetivo: Encontrar os coeficientes \(\beta_0\), \(\beta_1\) e \(\beta_2\) da equação \(\hat{y} = \beta_0 + \beta_1 x + \beta_2 x^2\) que melhor se ajustam aos nossos dados.
2 🛠️ Importando as Bibliotecas
Vamos começar importando as bibliotecas necessárias:
3 📊 Inserindo os Dados
Vamos trabalhar com dados que apresentam uma relação quadrática. Ao invés de digitarmos os dados diretamente \(y\) e \(x\) como listas, iremos ler os dados a partir de um arquivo que está disponível no link regressao_polinomial_exemplo. O arquivo esta no formato .csv em que cada coluna é separada por uma vírgula, um tipo de formatação muito comum.
df = pd.read_csv('https://raw.githubusercontent.com/FCopf/datasets/refs/heads/main/regressao_polinomial_exemplo.csv')Utilizando a função read_csv() da bilbioteca Pandas, os dados foram importados no formato de data frame, basicamento uma estrutura de dados em linhas e colunas, em que as colunas são denominadas de atributos.
print(df) x y
0 0 5
1 1 2
2 2 10
3 3 8
4 4 15
5 5 354 📈 Visualizando os Dados
Antes de ajustar o modelo, vamos visualizar nossos dados:
# Criando the gráfico de dispersão
plt.figure(figsize=(8, 6))
sns.scatterplot(data = df, x = 'x', y = 'y', color = '#0072B2', s=120, label='Dados observados')
# Configurando o gráfico
plt.title('Gráfico de Dispersão dos Dados', fontsize=14, fontweight='bold')
plt.xlabel('Variável X', fontsize=12)
plt.ylabel('Variável Y', fontsize=12)
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()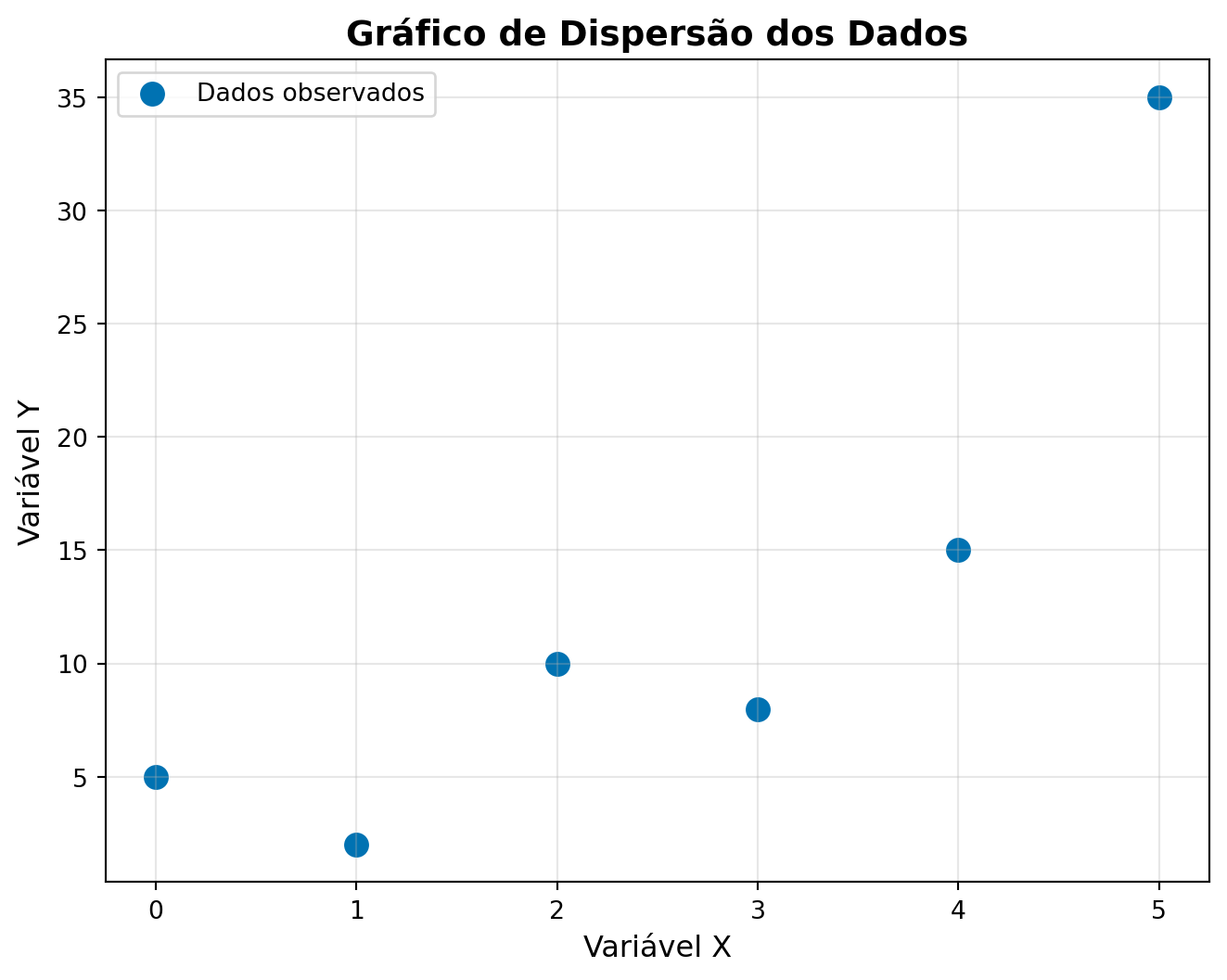
📝 Observação 1: Aparentemente, um modelo polinomial de segundo grau pode oferecer um ajuste melhor a estes dados do que a regressão linear simples. Nosso objetivo será explorar esse modelo e, ao final, compará-lo com o modelo linear.
📝 Observação 2: Como importamos os dados diretamente de um arquivo .csv para o objeto df, utilizamos a função scatterplot da biblioteca Seaborn para plotar o gráfico de dispersão entre as variáveis \(y\) e \(x\).
5 🧮 Implementando o MMQ Polinomial - Passo a Passo
5.1 Criando os Vetores Base
Para o modelo polinomial \(\hat{y} = \beta_0 + \beta_1 x + \beta_2 x^2\), precisamos dos vetores:
\[\vec{f}_0 = \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix} \quad \text{,} \quad \vec{f}_1 = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \quad \text{,} \quad \vec{f}_2 = \begin{bmatrix} x_1^2 \\ x_2^2 \\ \vdots \\ x_n^2 \end{bmatrix} \quad \text{e} \quad \vec{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}\]
# Número de observações
n = len(df['x'])
# Vetor f0: vetor de 1's (para o intercepto β₀)
f0 = [1] * n
# Vetor f1: valores de x (para o coeficiente linear β₁)
f1 = df['x'].copy()
# Vetor f2: valores de x² (para o coeficiente quadrático β₂)
f2 = np.array(df['x'])**2 # Eleva cada elemento de x ao quadradoVisualizando os vetores \(\vec{f}_0\), \(\vec{f}_1\) e \(\vec{f}_2\).
print("Vetor f0 (intercepto):", f0)
print("Vetor f1 (termo linear):", f1)
print("Vetor f2 (termo quadrático):", f2)Vetor f0 (intercepto): [1, 1, 1, 1, 1, 1]
Vetor f1 (termo linear): 0 0
1 1
2 2
3 3
4 4
5 5
Name: x, dtype: int64
Vetor f2 (termo quadrático): [ 0 1 4 9 16 25]5.2 Construindo as Matrizes X e Y
Agora vamos montar as matrizes do sistema polinomial:
\[X = \begin{bmatrix} \vec{f}_0 & \vec{f}_1 & \vec{f}_2 \end{bmatrix} = \begin{bmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & x_n^2 \end{bmatrix} \quad \text{e} \quad Y = \begin{bmatrix} \vec{y} \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}\]
# Matriz X: combinando f0, f1 e f2 em colunas
X = np.column_stack((f0, f1, f2))
# Matriz Y: transformando y em matriz com n linhas e 1 coluna
Y = np.array(df['y']).reshape(n, 1)5.3 Resolvendo o Sistema Normal
Calculamos os coeficientes usando a mesma fórmula:
\[B = (X^T X)^{-1} X^T Y\]
# Calculando X transposta vezes X
XTX = X.T @ X # X.T é a transposta de X
# Calculando X transposta vezes Y
XTY = X.T @ Y
# Calculando a matriz inversa (X^T X)^(-1)
XTX_inv = np.linalg.inv(XTX) # Inversa de X^T X
# Coeficientes de regressão
B = XTX_inv @ XTY
NotaInterpretação
- \(\beta_0\) (intercepto): valor de y quando x = 0
- \(\beta_1\) (coeficiente linear): relacionado à taxa de variação linear
- \(\beta_2\) (coeficiente quadrático): relacionado à curvatura da parábola
- Se \(\beta_2 > 0\): parábola com concavidade para cima
- Se \(\beta_2 < 0\): parábola com concavidade para baixo
5.4 Obtendo os Valores Ajustados de y
Tendo obtido os coeficientes de regressão, os valores ajustados de y (\(\hat{y}\)) podem ser obtido pela multiplicação matricial:
\[F = XB = \begin{bmatrix} 1 & x_1 & x^2_1 \\ 1 & x_2 & x^2_2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & x^2_n \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \end{bmatrix}\]
Obs.: denominamos \(F\) a matriz de valores ajustados de \(y\).
# Valores ajustados (preditos)
F = X @ B5.5 Avaliando a Qualidade do Ajuste
5.5.1 Calculando a Soma dos Quadrados dos Resíduos (\(SQ_{res}\))
\(SQ_{res}\) pode ser obtida pela multiplicação matricial:
\[SQ_{res} = \boldsymbol{e}^T \boldsymbol{e}\]
Em que \(\boldsymbol{e}\) é a matriz coluna dos resíduos obtida pela diferença entre os valores observados e ajustados de \(y\):
\[\boldsymbol{e} = Y - F = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} - \begin{bmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_n \end{bmatrix} = \begin{bmatrix} e_1 \\ e_2 \\ \vdots \\ e_n \end{bmatrix}\]
# Resíduos: diferença entre valores observados e ajustados
e = Y - F
# Soma dos Quadrados dos Resíduos
SQres = (e.T @ e)[0, 0]5.5.2 Calculando a Soma dos Quadrados Totais (\(SQ_{tot}\))
\(SQ_{tot}\) pode ser obtida pela multiplicação matricial:
\[SQ_{tot} = \boldsymbol{D}^T \boldsymbol{D}\]
Em que \(\boldsymbol{D}\) é a matriz coluna dos desvios da médis obtida pela diferença entre os valores observados de \(y\) e a média de \(\overline{y}\):
\[\boldsymbol{D} = Y - \overline{Y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} - \begin{bmatrix} \overline{y} \\ \overline{y} \\ \vdots \\ \overline{y} \end{bmatrix} = \begin{bmatrix} d_1 \\ d_2 \\ \vdots \\ d_n \end{bmatrix}\]
# Soma dos Quadrados Total
Y_medio = np.mean(Y)
D = Y - Y_medio
SQtot = (D.T @ D)[0, 0]5.5.3 Calculando o coeficiente de determinação \(R^2\):
O \(R^2\) é dado pela expressão:
\[R^2 = 1 - \frac{SQ_{res}}{SQ_{tot}}\]
# Coeficiente de Determinação R²
R2 = 1 - (SQres / SQtot)Visualizando os resultados:
print("📊 Medidas de Qualidade do Ajuste:")
print(f"Soma dos Quadrados dos Resíduos (SQres): {SQres:.4f}")
print(f"Soma dos Quadrados Total (SQtot): {SQtot:.4f}")
print(f"Coeficiente de Determinação (R²): {R2:.4f}")
print(f"Porcentagem da variação explicada: {R2*100:.2f}%")📊 Medidas de Qualidade do Ajuste:
Soma dos Quadrados dos Resíduos (SQres): 59.2643
Soma dos Quadrados Total (SQtot): 705.5000
Coeficiente de Determinação (R²): 0.9160
Porcentagem da variação explicada: 91.60%6 📊 Visualizando o Resultado Final
Vamos plotar os dados originais junto com a curva ajustada:
Criando uma linha contínua para \(\hat{y}\)
# Criando pontos para desenhar a curva suave
x_curva = np.linspace(min(df['x']), max(df['x']), 100)
y_curva = B[0, 0] + B[1, 0] * x_curva + B[2, 0] * x_curva**2# Criando o gráfico final
plt.figure(figsize=(8, 6))
# Pontos observados
sns.scatterplot(data = df, x = 'x', y = 'y',
color = '#0072B2', s=120,
label=f'Dados observados (n={n})')
# Valores ajustados
plt.scatter(df['x'], F[:,0],
color='#000000', marker='*', s=120,
label='Valores ajustados')
# Curva ajustada
plt.plot(x_curva, y_curva,
color='#D55E00',
label=fr'Curva ajustada: $\hat{{y}} = {B[0,0]:.3f} {B[1,0]:.3f}x + {B[2,0]:.3f}x^2$')
# Configurações do gráfico
plt.title(f'Regressão Polinomial (2º grau) - MMQ\nR² = {R2:.4f}',
fontsize=15, fontweight='bold')
plt.xlabel('Variável X', fontsize=12)
plt.ylabel('Variável Y', fontsize=12)
plt.grid(True, alpha=0.3)
plt.legend(fontsize=10)
plt.tight_layout()
plt.show()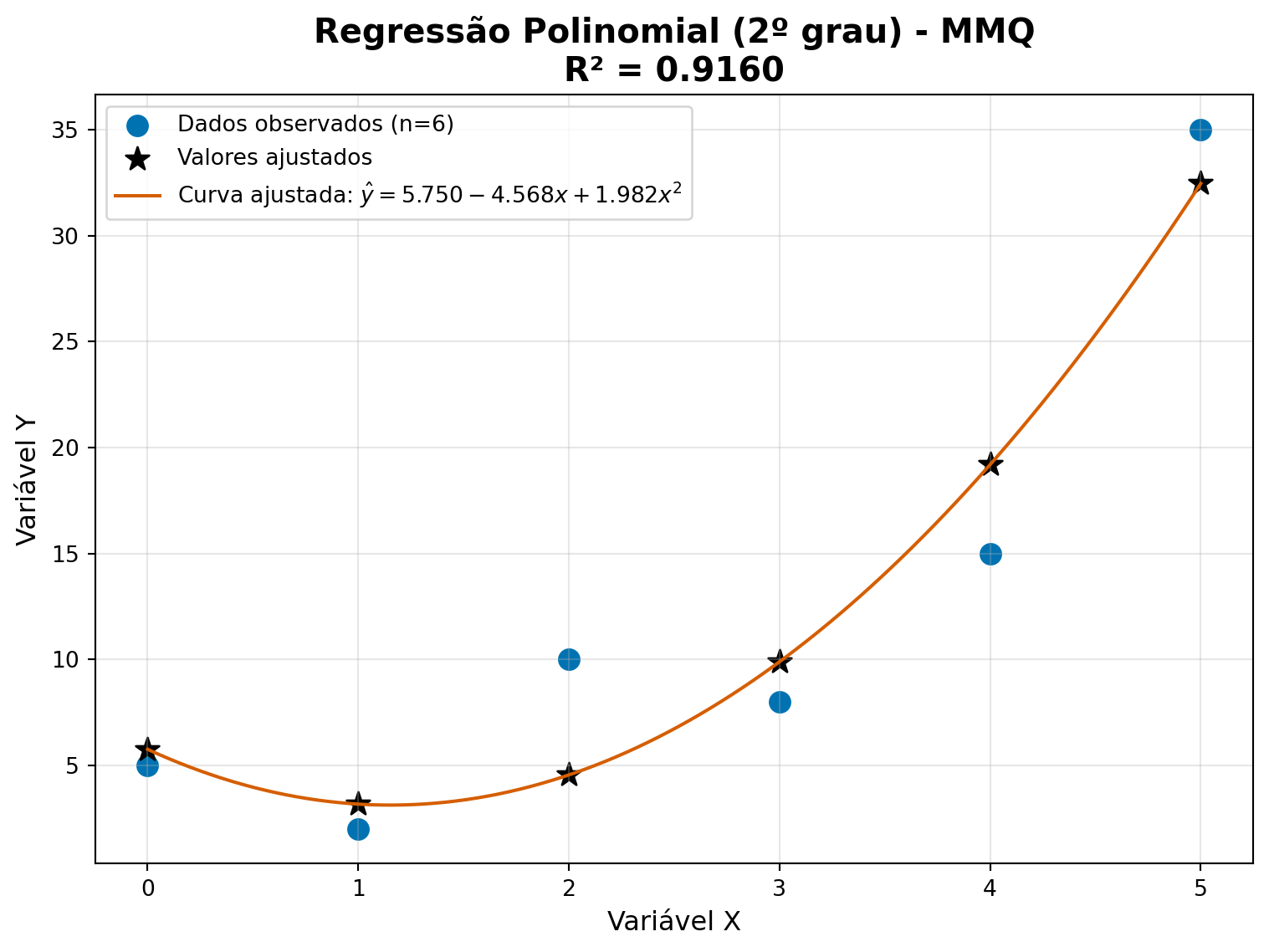
7 🎯 Resumo dos Resultados
print("="*60)
print(" RESUMO DA REGRESSÃO POLINOMIAL")
print("="*60)
print(f"Equação ajustada: y = {B[0,0]:.4f} {B[1,0]:.4f}x + {B[2,0]:.4f}x²")
print(f"Coeficiente de determinação (R²): {R2:.4f}")
print(f"Porcentagem da variação explicada: {R2*100:.2f}%")
print("="*60)============================================================
RESUMO DA REGRESSÃO POLINOMIAL
============================================================
Equação ajustada: y = 5.7500 -4.5679x + 1.9821x²
Coeficiente de determinação (R²): 0.9160
Porcentagem da variação explicada: 91.60%
============================================================8 🔍 Comparação: Linear vs Polinomial
Vamos comparar o ajuste linear e polinomial para os mesmos dados:
# Ajuste LINEAR para comparação
X_linear = np.column_stack((f0, f1)) # Apenas f0 e f1
B_linear = np.linalg.inv(X_linear.T @ X_linear) @ (X_linear.T @ Y)
# R² do modelo linear
F_linear = X_linear @ B_linear
residuos_linear = Y - F_linear
SQres_linear = (residuos_linear.T @ residuos_linear)[0, 0]
R2_linear = 1 - (SQres_linear / SQtot)
print("📊 Comparação dos Modelos:")
print("-" * 40)
print(f"Modelo Linear: R² = {R2_linear:.4f}")
print(f"Modelo Polinomial: R² = {R2:.4f}")
print(f"Melhoria no R²: {R2 - R2_linear:.4f}")📊 Comparação dos Modelos:
----------------------------------------
Modelo Linear: R² = 0.7081
Modelo Polinomial: R² = 0.9160
Melhoria no R²: 0.2079Gráficos de dispersão
y_linear = B_linear[0, 0] + B_linear[1, 0] * np.array(df['x'])
# Gráfico comparativo
plt.figure(figsize=(8, 6))
# plt.subplot(1, 2, 1)
sns.scatterplot(data = df, x = 'x', y = 'y', s=100, color = '#0072B2', label='Dados observados')
plt.plot(df['x'], y_linear, color='#D55E00', label=f'Modelo Linear\nR² = {R2_linear:.4f}')
plt.plot(x_curva, y_curva, color='#009E73', label=f'Modelo Polinomial\nR² = {R2:.4f}')
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True, alpha=0.3)
plt.legend()
# plt.tight_layout()
plt.show()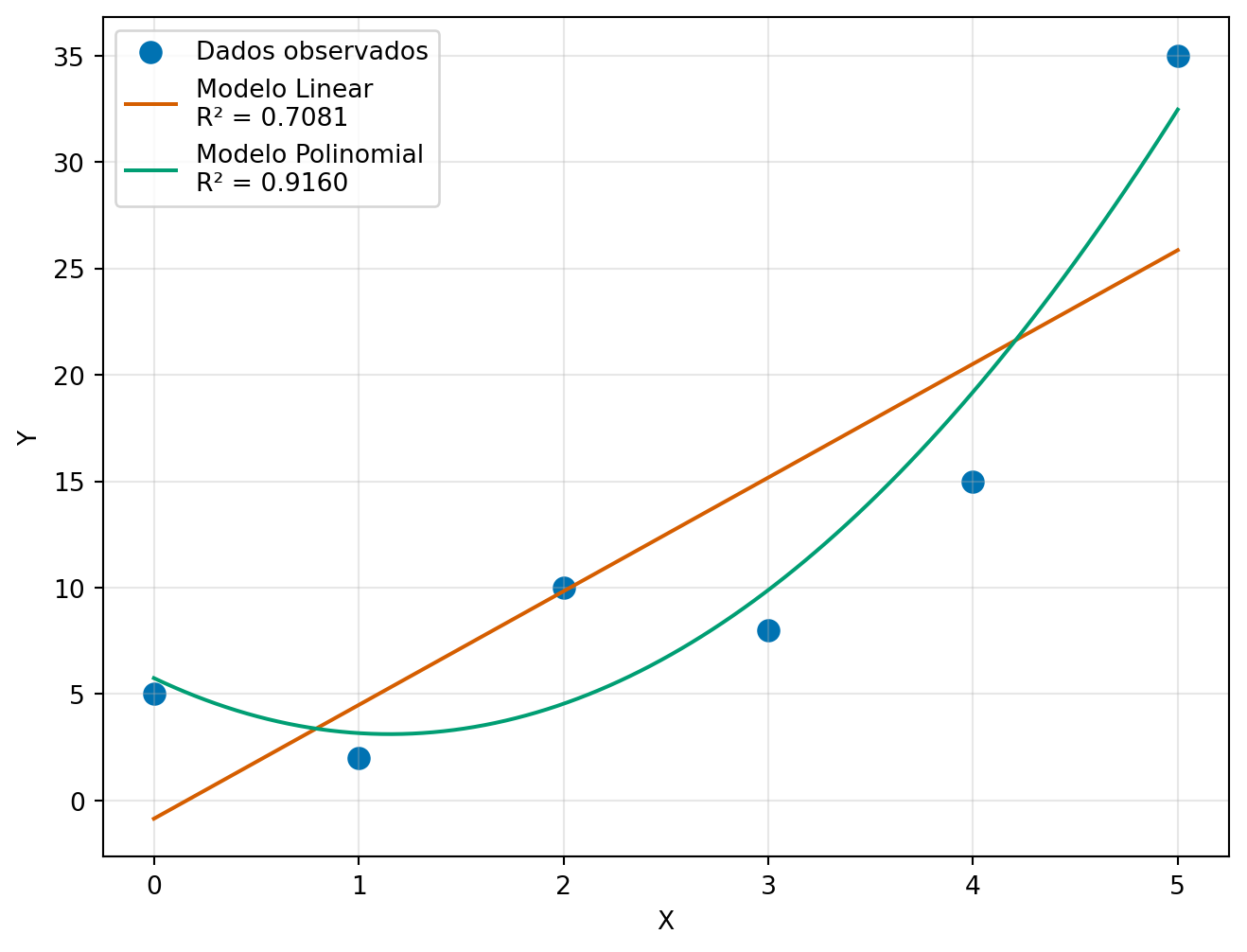
9 🧾 Resumo do Código (modelo polinomial)
- Inserção dos Dados
df = pd.read_csv('https://raw.githubusercontent.com/FCopf/datasets/refs/heads/main/regressao_polinomial_exemplo.csv')- Definição das matrizes do sistema
n = len(df['x'])
f0 = [1] * n
f1 = df['x'].copy()
f2 = np.array(df['x'])**2
X = np.column_stack((f0, f1, f2))
Y = np.array(df['y']).reshape(n, 1)- Cálculo dos coeficientes
XTX = X.T @ X
XTY = X.T @ Y
XTX_inv = np.linalg.inv(XTX)
B = XTX_inv @ XTY- Qualidade do ajuste
Y_ajustado = X @ B
e = Y - Y_ajustado
SQres = (e.T @ e)[0, 0]
Y_medio = np.mean(Y)
D = Y - Y_medio
SQtot = (D.T @ D)[0, 0]
R2 = 1 - (SQres / SQtot)10 🚀 Exercício Prático
Teste o código com novos dados:
# Experimente com estes dados (padrão quadrático diferente):
df_novo = pd.DataFrame({
'x_novo': [1, 2, 3, 4, 5, 6, 7],
'y_novo': [30, 12, 18, 9, 7, 8, 6]
})
print(df_novo)
# Questões para investigar:
# 1. Qual é o R² do modelo polinomial para estes dados?
# 2. O coeficiente β₂ é positivo ou negativo? O que isso significa?
# 3. Compare com o modelo linear - qual é a diferença no R²?
# Implemente todo o processo do MMQ polinomial com os novos dados
# Dica: você pode copiar e adaptar o código acima! x_novo y_novo
0 1 30
1 2 12
2 3 18
3 4 9
4 5 7
5 6 8
6 7 611 💡 Conceitos Importantes Revisados
- Regressão Polinomial: Extensão da regressão linear para relações curvas
- Matriz de Design: Agora com três colunas: \([1, x, x^2]\)
- Interpretação dos Coeficientes: Cada coeficiente tem significado específico
- Comparação de Modelos: Uso do \(R^2\) para avaliar qual modelo é melhor
12 🔗 Próximos Passos
- Experimente com polinômios de grau maior (\(x^3\), \(x^4\), etc.)
- Investigue o conceito de overfitting com graus muito altos