Modelos Estatísticos e Modelos Científicos

Complexidade Tecnológica em Ilhas da Oceania

Três estratégias para modelar a relação entre tamanho populacional e número de ferramentas

Vamos utilizar modelos estatísticos para analisar a complexidade tecnológica tradicional em ilhas da Oceania (Kline e Boyd 2010). Nosso objetivo é compreender como o tamanho populacional influenciou o número de ferramentas disponíveis em cada sociedade.

Compararemos três estratégias de modelagem, todas implementadas com PyMC:

Modelo Linear com Transformação Logarítmica: Utilizando regressão linear após transformar as variáveis
Modelo Linear Generalizado (GLM): Especificamente regressão de Poisson para dados de contagem
Modelo Científico (Mecanicista): Baseado em uma descrição teórica da dinâmica de aquisição e perda de ferramentas (McElreath 2018)

1 Analisando o conjunto de dados

Importe os dados kline.csv.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pymc as pm
import bambi as bmb
import arviz as az
import xarray as xr

kline = pd.read_csv('https://raw.githubusercontent.com/FCopf/datasets/refs/heads/main/kline.csv')
kline

	culture	population	contact	total_tools	mean_TU	lat	lon
0	Malekula	1100	low	13	3.2	-16.3	167.5
1	Tikopia	1500	low	22	4.7	-12.3	168.8
2	Santa Cruz	3600	low	24	4.0	-10.7	166.0
3	Yap	4791	high	43	5.0	9.5	138.1
4	Lau Fiji	7400	high	33	5.0	-17.7	178.1
5	Trobriand	8000	high	19	4.0	-8.7	150.9
6	Chuuk	9200	high	40	3.8	7.4	151.6
7	Manus	13000	low	28	6.6	-2.1	146.9
8	Tonga	17500	high	55	5.4	-21.2	-175.2
9	Hawaii	275000	low	71	6.6	19.9	-155.6

Visualize a relação entre tamanho populacional (P) e número total de ferramentas (T).

# Definir tema com fonte maior
plt.figure(figsize=(8, 6))
sns.scatterplot(data=kline, x='population', y='total_tools', 
                s=100, alpha=0.7, color='#1f77b4')

# Personalização dos rótulos e tema
plt.xlabel('Tamanho populacional', fontsize=14)
plt.ylabel('Número total de ferramentas', fontsize=14)
sns.set_theme(style="whitegrid")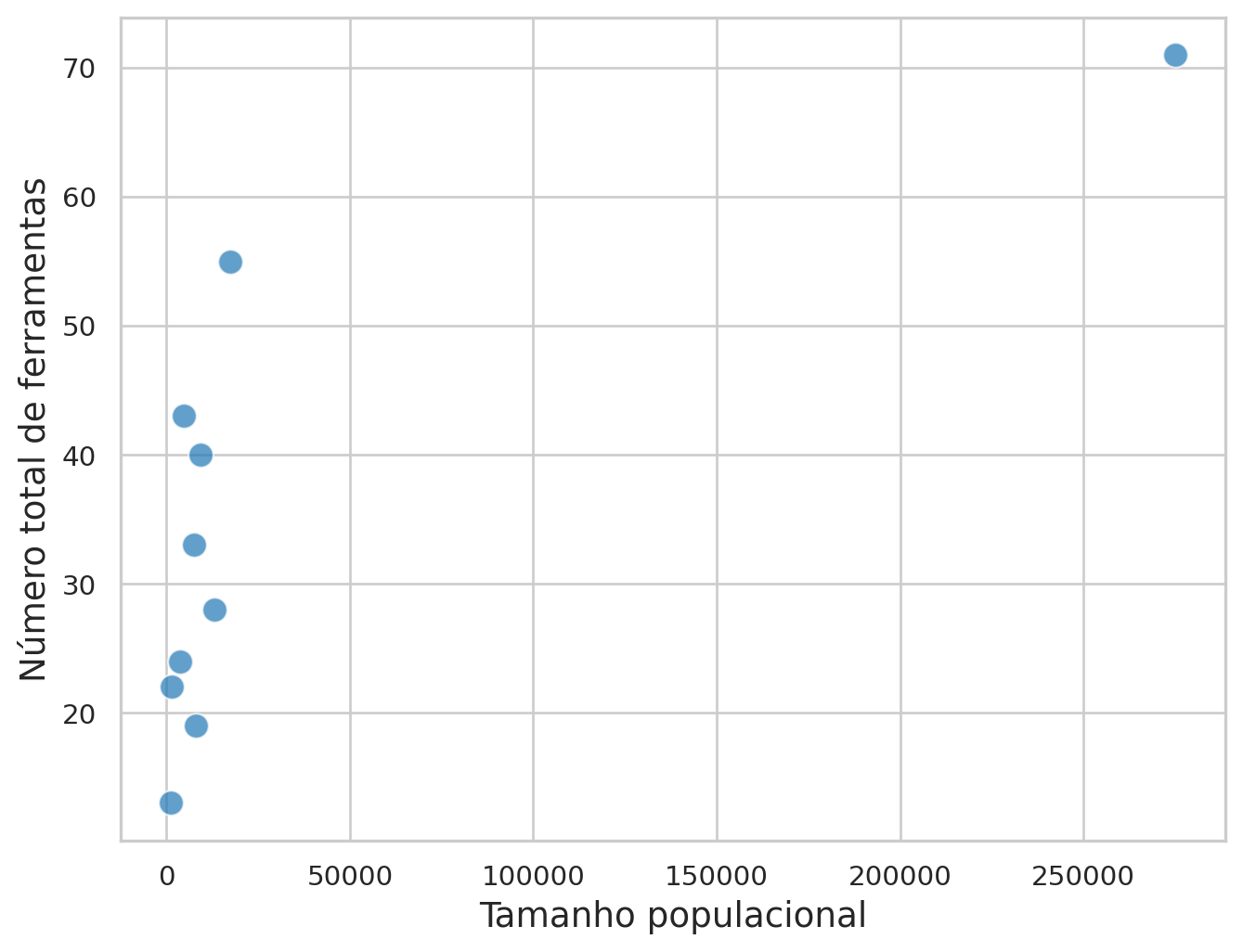

Figura 1: Relação entre o número total de ferramentas e o tamanho populacional em ilhas na Oceania

2 Estratégia 1: Regressão Linear com Transformação Logarítmica

A relação na Figura 1 é claramente não linear e pode ser descrita por:

\[T = \beta_0P^{\beta_1}\]

Uma alternativa simples neste caso é utilizar uma transformação logarítmica para linearizar a expressão:

\[\log(T) = \log(\beta_0P^{\beta_1}) \Rightarrow \log(T) = \log(\beta_0) + \log(P^{\beta_1}) \Rightarrow\]

\[\log(T) = B_0 + \beta_1 \log(P) \tag{1}\]

em que \(B_0 = \log(\beta_0)\)

Visualizando na escala logarítmica:

kline['log_tools'] = np.log(kline['total_tools'])
kline['log_pop'] = np.log(kline['population'])

plt.figure(figsize=(8, 6))
sns.scatterplot(data=kline, x='log_pop', y='log_tools', 
                s=100, alpha=0.7, color='#1f77b4')

# Personalização dos rótulos e tema
plt.xlabel('log do Tamanho populacional', fontsize=14)
plt.ylabel('log do Número total de ferramentas', fontsize=14)

(a) Relação entre o logarítmo do número total de ferramentas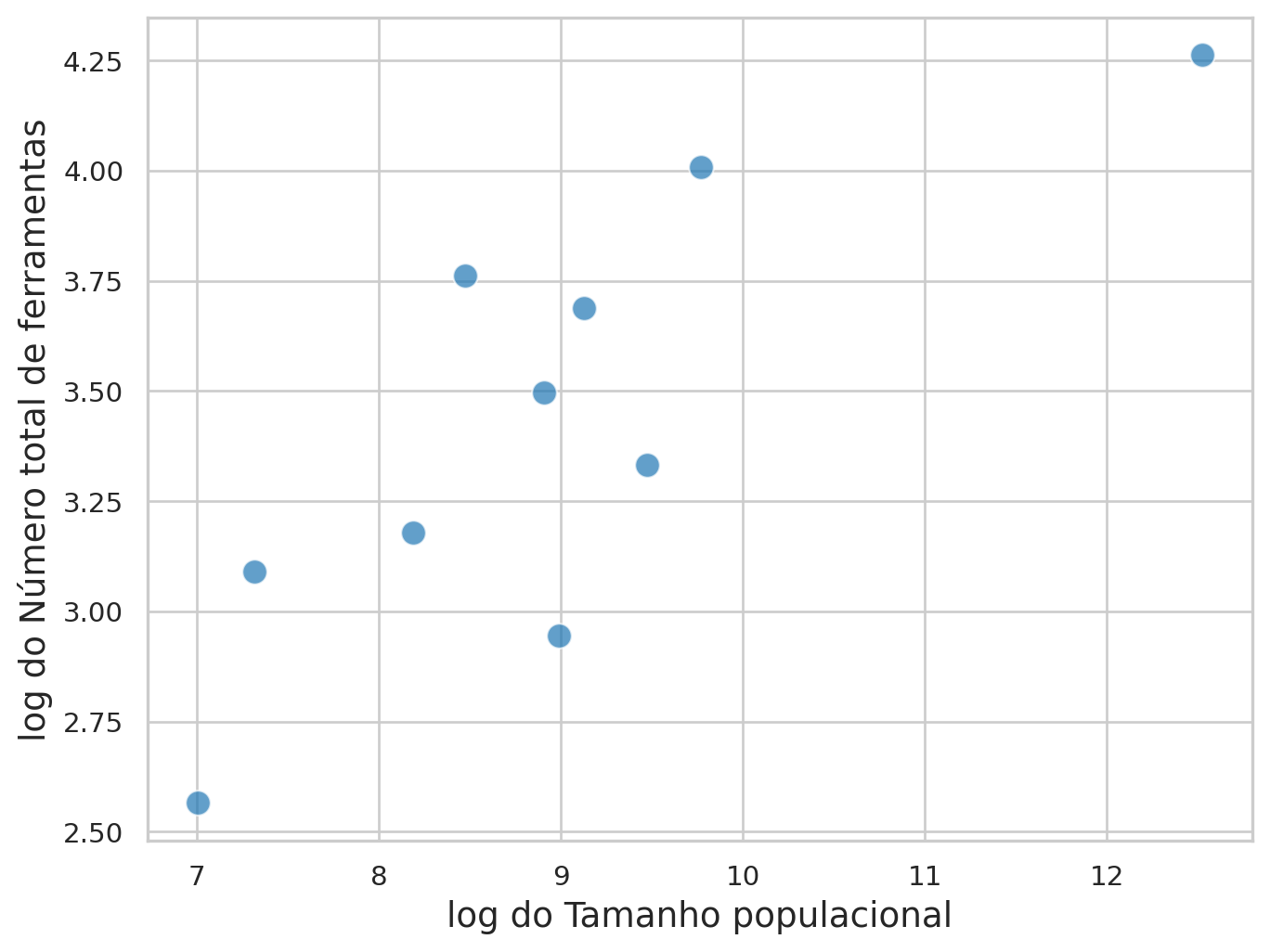 e o logarítmo do tamanho populacional

Considerando que a relação na Figura 2 é aproximadamente linear, vamos ajustar o modelo de regressão linear descrito na Equação 1.

Neste modelo, estamos assumindo que \(\log(T)\) é uma variável aleatória normnalmente distribuída:

\[\log(T) \sim \mathcal{N}(\mu,\,\sigma)\]

\[\mu = B_0 + \beta_1 \log(P)\]

2.1 Implementação

mlinear = bmb.Model("log_tools ~ log_pop", data=kline)
trace_linear = mlinear.fit()

# Resumo dos parâmetros
az.summary(trace_linear)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
sigma	0.367	0.105	0.208	0.557	0.002	0.003	2459.0	2370.0	1.0
Intercept	0.989	0.752	-0.449	2.410	0.015	0.021	2836.0	1925.0	1.0
log_pop	0.272	0.083	0.115	0.434	0.002	0.002	2798.0	1931.0	1.0

2.2 Gerando predições do modelo linear

pred_linear = mlinear.predict(trace_linear, kind = 'response', data = kline, inplace=False)
pred_linear_draws = pred_linear.posterior_predictive.log_tools
pred_linear_mean = pred_linear_draws.mean(dim=['chain', 'draw'])

2.3 Visualização do modelo linear

plt.figure(figsize=(8, 6))
sns.scatterplot(data=kline, x='log_pop', y='log_tools', 
                s=100, alpha=0.7, color='#1f77b4')

plt.plot(kline['log_pop'],pred_linear_mean.values, color='red', linewidth=2, label='Predição média')
az.plot_hdi(
    kline['log_pop'],
    pred_linear.posterior_predictive.log_tools,
    hdi_prob=0.95, # Intervalo de 95%
    color='#f3ae1a',
    fill_kwargs={'alpha': 0.3, 'label': 'Intervalo de Credibilidade (95%)'}
)

plt.xlabel('log(População)', fontsize=14)
plt.ylabel('Número total de ferramentas', fontsize=14)
plt.title('Modelo de linear: log_tools ~ log_pop', fontsize=16)
plt.legend()
plt.grid(True, alpha=0.3)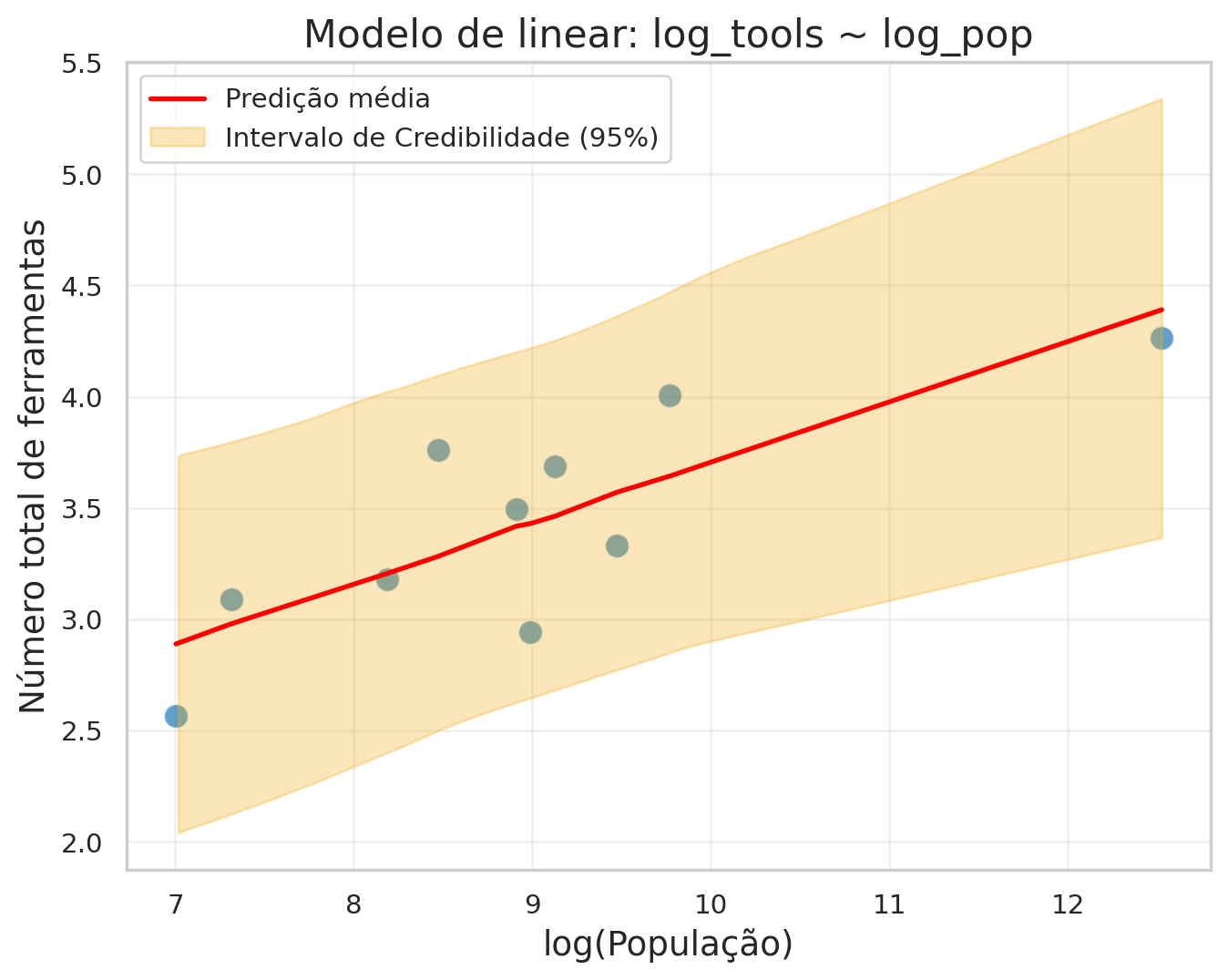

2.3.1 Visualização do modelo linear na escala original

Como a escala original é um modelo não linear, teremos que gerar os valores preditos para mais pontos a partir dos parâmetros estimaos

log_pop = np.linspace(min(kline['log_pop']), np.max(kline['log_pop']), num=1000)
new_x =  xr.DataArray(
    log_pop,
    dims=['obs'],
    coords={'obs': range(len(log_pop))},
    name='log_pop'
)

mlinear_pars = mlinear.predict(trace_linear, kind = 'response_params', data = kline, inplace=False)

B0 = mlinear_pars.posterior['Intercept']
b1 = mlinear_pars.posterior['log_pop']
new_pred_linear_mean = B0.values.mean() + b1.values.mean() * new_x

new_pred_linear = np.exp(B0 + b1 * new_x)
ic_linear = az.hdi(new_pred_linear, hdi_prob=0.95)

plt.figure(figsize=(8, 6))
sns.scatterplot(data=kline, x='population', y='total_tools', 
                s=100, alpha=0.7, color='#1f77b4')

plt.plot(np.exp(new_x),np.exp(new_pred_linear_mean))

plt.fill_between(np.exp(new_x),
                 ic_linear.sel(hdi='lower')['x'],
                 ic_linear.sel(hdi='higher')['x'],
                 alpha=0.3, color='#f3ae1a', 
                 label='HDI 95%')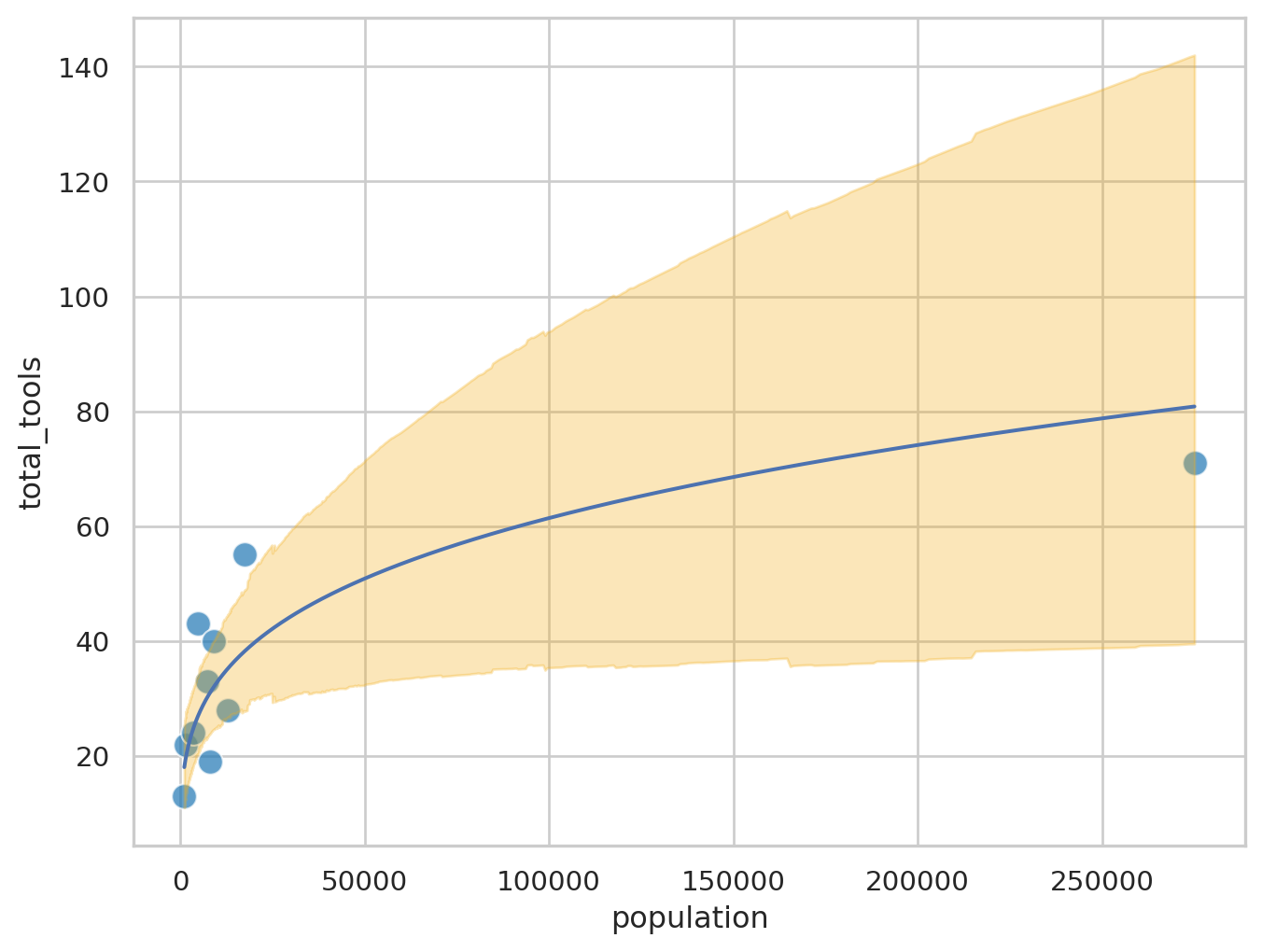

3 Estratégia 2: Regressão de Poisson (GLM)

Embora a transformação logarítmica torne linear a porção determinística do modelo, ela não resolve adequadamente a natureza discreta da variável de resposta. No caso do número de ferramentas (total_tools), estamos lidando com dados de contagem — valores inteiros não negativos. Uma abordagem mais apropriada é utilizar uma regressão de Poisson, que modela diretamente a distribuição da variável como uma variável aleatória de contagem.

Vamos assumir que o que realmente influencia a diversidade tecnológica não é o tamanho absoluto da população, mas sim sua ordem de grandeza (Kline e Boyd 2010). Espera-se, portanto, uma associação positiva entre o número de ferramentas e o logaritmo do tamanho populacional.

Este modelo generativo pode ser descrito como:

\[T_i \sim \text{Poisson}(\lambda_i)\]

\[\log(\lambda_i) = \beta_0 + \beta_1 \cdot \log(P_i)\]

Onde: * \(T_i\) é o número de ferramentas na sociedade i * \(P_i\) é o tamanho populacional * A função de ligação logarítmica garante que \(\lambda_i > 0\)

3.1 Implementação

mpoisson = bmb.Model("total_tools ~ log_pop", 
                     data=kline, 
                     family="poisson")

trace_poisson = mpoisson.fit(draws=2000, tune=1000)

# Resumo dos parâmetros
az.summary(trace_poisson)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
Intercept	1.333	0.307	0.757	1.905	0.004	0.003	6893.0	5122.0	1.0
log_pop	0.239	0.032	0.181	0.299	0.000	0.000	6870.0	5334.0	1.0

3.2 Gerando predições do modelo Poisson

# Predições para os dados originais
pred_poisson = mpoisson.predict(trace_poisson, kind='response', data=kline, inplace=False)
pred_poisson_draws = pred_poisson.posterior_predictive.total_tools
pred_poisson_mean = pred_poisson_draws.mean(dim=['chain', 'draw'])

# Criar dados para predição suave
log_pop_new = np.linspace(min(kline['log_pop']), max(kline['log_pop']), num=100)
new_data = pd.DataFrame({'log_pop': log_pop_new})

# Gerar predições
new_pred_poisson = mpoisson.predict(trace_poisson, kind='response', data=new_data, inplace=False)
new_pred_poisson_mean = new_pred_poisson.posterior_predictive.total_tools.mean(dim=['chain', 'draw'])

3.3 Visualização do modelo Poisson

plt.figure(figsize=(8, 6))

# Pontos originais
sns.scatterplot(data=kline, x='log_pop', y='total_tools', 
                s=100, alpha=0.7, color='#1f77b4', label='Dados observados')

# Linha de predição média
plt.plot(log_pop_new, new_pred_poisson_mean.values, 
         color='red', linewidth=2, label='Predição média')

# Intervalo de credibilidade
az.plot_hdi(
    log_pop_new,
    new_pred_poisson.posterior_predictive.total_tools,
    hdi_prob=0.95,
    color='#f3ae1a',
    fill_kwargs={'alpha': 0.3, 'label': 'HDI 95%'}
)

plt.xlabel('log(População)', fontsize=14)
plt.ylabel('Número total de ferramentas', fontsize=14)
plt.title('Modelo de Poisson: total_tools ~ log_pop', fontsize=16)
plt.legend()
plt.grid(True, alpha=0.3)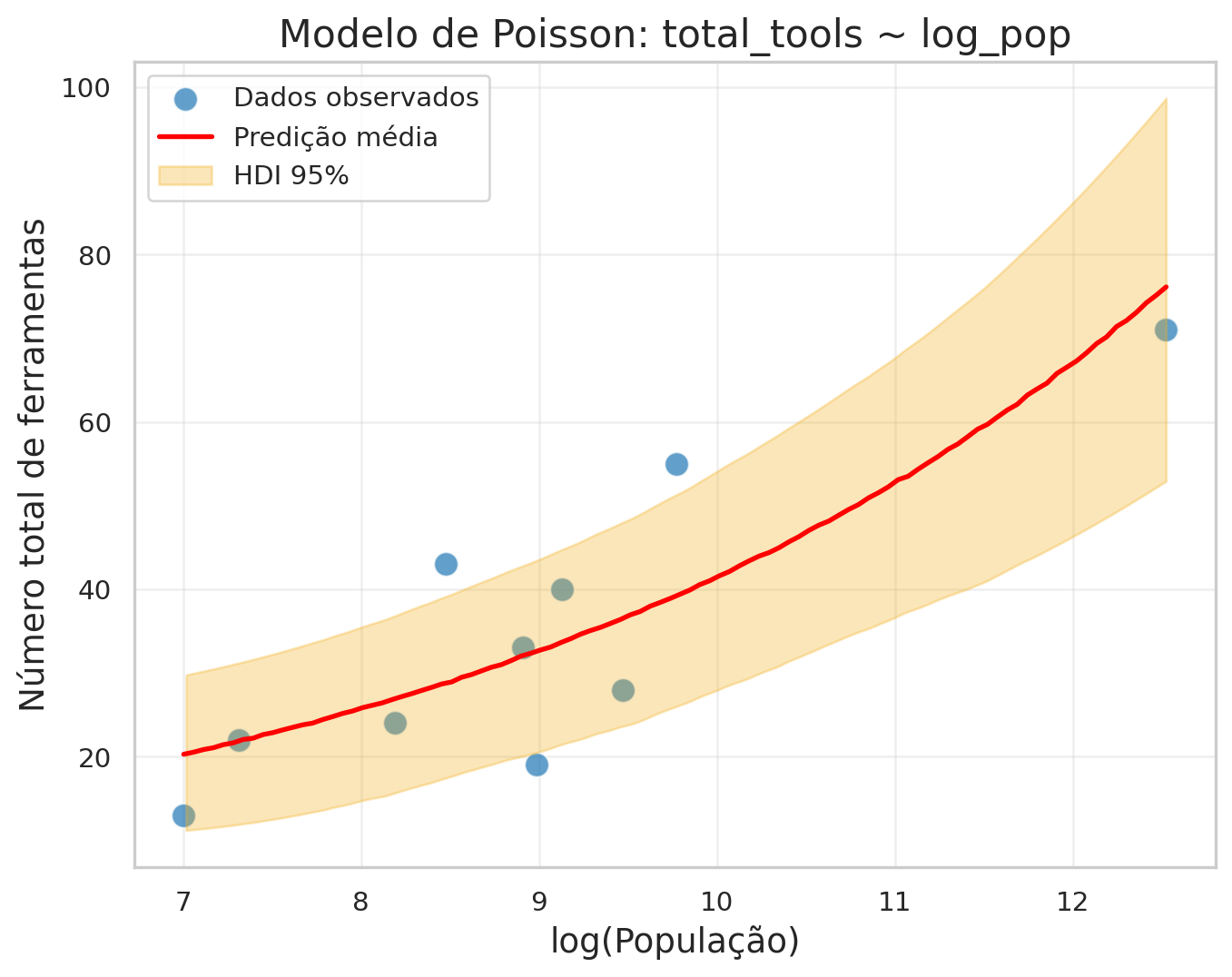

3.4 Visualização na escala original (população)

plt.figure(figsize=(12, 8))

sns.scatterplot(data=kline, x='population', y='total_tools', 
                s=100, alpha=0.7, color='black', label='Dados observados')

plt.plot(np.exp(log_pop_new), new_pred_poisson_mean.values, 
         color='blue', linewidth=2, linestyle='--', label='Modelo Poisson')
az.plot_hdi(
    np.exp(log_pop_new),
    new_pred_poisson.posterior_predictive.total_tools,
    hdi_prob=0.95,
    color='#1f77b4',
    fill_kwargs={'alpha': 0.3, 'label': 'HDI 95% Poisson'},
)

plt.xlabel('População', fontsize=14)
plt.ylabel('Número total de ferramentas', fontsize=14)
plt.title('Comparação de Modelos', fontsize=16)
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()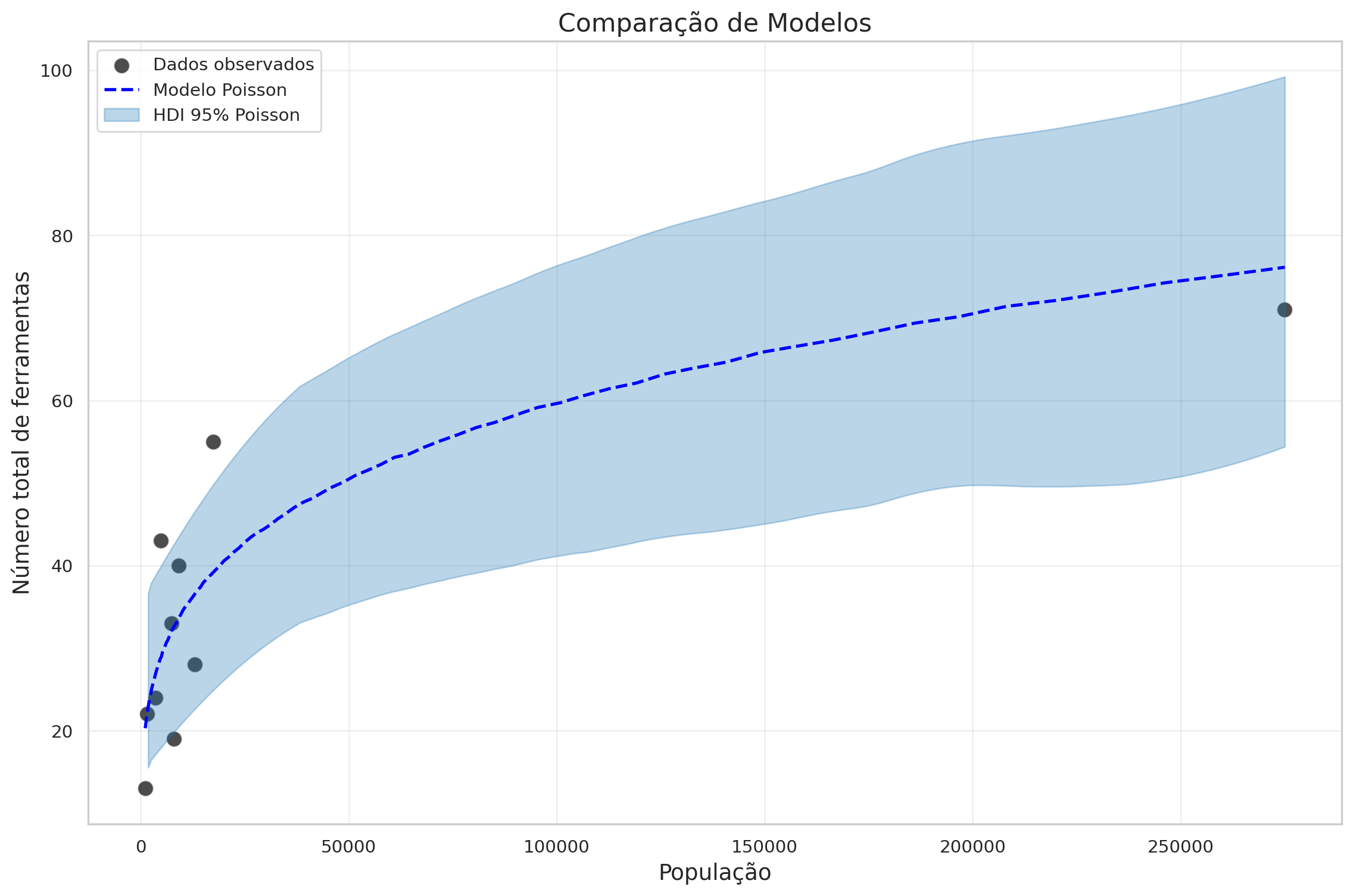

3.5 Comparação com modelo linear

plt.figure(figsize=(12, 8))

sns.scatterplot(data=kline, x='population', y='total_tools', 
                s=100, alpha=0.7, color='black', label='Dados observados')

# Modelo Linear com transformação log (escala original)
plt.plot(np.exp(new_x), np.exp(new_pred_linear_mean), 
         color='red', linewidth=2, label='Modelo Linear')
plt.fill_between(np.exp(new_x),
                 ic_linear.sel(hdi='lower')['x'],
                 ic_linear.sel(hdi='higher')['x'],
                 alpha=0.3, color='#f3ae1a', 
                 label='HDI 95% Linear')

# Modelo Poisson (GLM)
plt.plot(np.exp(log_pop_new), new_pred_poisson_mean.values, 
         color='blue', linewidth=2, linestyle='--', label='Modelo Poisson')
az.plot_hdi(
    np.exp(log_pop_new),
    new_pred_poisson.posterior_predictive.total_tools,
    hdi_prob=0.95,
    color='#1f77b4',
    fill_kwargs={'alpha': 0.3, 'label': 'HDI 95% Poisson'},
)

plt.xlabel('População', fontsize=14)
plt.ylabel('Número total de ferramentas', fontsize=14)
plt.title('Comparação de Modelos', fontsize=16)
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()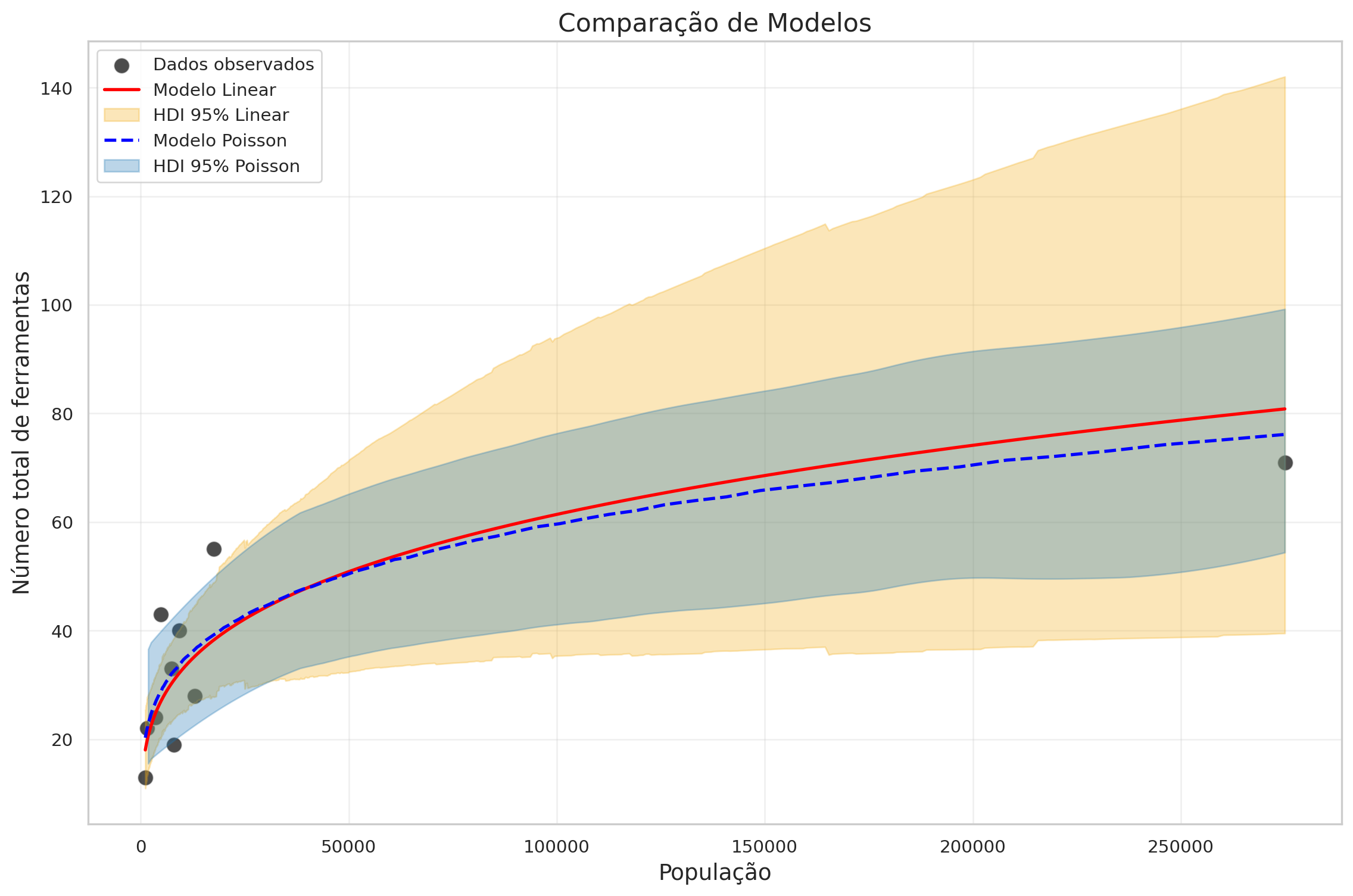

4 Estratégia 3: Modelo Científico (Mecanicista)

Partindo de uma descrição teórica da dinâmica de inovação tecnológica, podemos expressar a mudança esperada no número de ferramentas ao longo do tempo como:

\[\Delta T = \alpha P^\beta - \gamma T\]

Onde: * \(P\) é o tamanho da população * \(T\) é o número de ferramentas * \(\alpha\), \(\beta\) e \(\gamma\) são parâmetros a serem estimados * \(\alpha P^\beta\) representa a taxa de inovação (dependente da população) * \(\gamma T\) representa a taxa de perda de ferramentas

Assumindo que o sistema está em equilíbrio (\(\Delta T = 0\)), podemos resolver para \(T\):

Situação de equilíbrio

Começamos com: \[0 = \alpha P^\beta - \gamma T\]

Isolando o termo \(T\): \[\gamma T = \alpha P^\beta\]

Dividindo ambos os lados por \(\gamma\): \[T = \frac{\alpha P^\beta}{\gamma} \tag{2}\]

Incorporando a Equação 2 a um modelo de Poisson:

\[T_i \sim \text{Poisson}(\lambda_i)\]

\[\lambda_i = \frac{\alpha P_i^{\beta}}{\gamma}\]

4.1 Implementação em PyMC

Para facilitar a implementação, vamos reparametrizar usando:

\[\log(\lambda_i) = \log(\alpha) + \beta \cdot \log(P_i) - \log(\gamma)\]

ou equivalentemente:

\[\log(\lambda_i) = \theta_\alpha + \beta \cdot \log(P_i) + \theta_\gamma\]

onde \(\theta_\alpha = \log(\alpha)\) e \(\theta_\gamma = -\log(\gamma)\).

log_pop = np.log(kline['population'])
tools = kline['total_tools'].values

with pm.Model() as scientific_model:
    # Priors
    theta_alpha = pm.Normal("theta_alpha", mu=0, sigma=2)
    beta = pm.Normal("beta", mu=0, sigma=1)
    theta_gamma = pm.Normal("theta_gamma", mu=0, sigma=1)

    # Esperança em escala log
    log_lambda = theta_alpha + beta * log_pop + theta_gamma
    lambda_ = pm.math.exp(log_lambda)

    # Likelihood
    T_obs = pm.Poisson("total_tools", mu=lambda_, observed=tools)

    # Amostragem
    trace_scientific = pm.sample(2000, tune=1000, target_accept=0.95)
    pm.compute_log_likelihood(trace_scientific)

az.summary(trace_scientific, var_names=["theta_alpha", "beta", "theta_gamma"], hdi_prob=0.89)

	mean	sd	hdi_5.5%	hdi_94.5%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
theta_alpha	1.037	0.941	-0.567	2.440	0.020	0.015	2175.0	2261.0	1.0
beta	0.241	0.031	0.192	0.290	0.001	0.000	2905.0	2778.0	1.0
theta_gamma	0.276	0.920	-1.114	1.813	0.019	0.016	2256.0	2236.0	1.0

4.2 Gerando predições do modelo científico

posterior = trace_scientific.posterior

# Recuperar parâmetros transformados
alpha_samples = np.exp(posterior['theta_alpha'])
beta_samples = posterior['beta']
gamma_samples = np.exp(-posterior['theta_gamma'])

# Grid de população para predições
pop_pred = np.linspace(kline['population'].min(), kline['population'].max(), 200)

# Calcular predições usando a fórmula científica
pred_samples = []
for i in range(len(alpha_samples.chain)):
    for j in range(len(alpha_samples.draw)):
        alpha_val = alpha_samples.isel(chain=i, draw=j).values
        beta_val = beta_samples.isel(chain=i, draw=j).values
        gamma_val = gamma_samples.isel(chain=i, draw=j).values
        
        pred = (alpha_val * (pop_pred ** beta_val)) / gamma_val
        pred_samples.append(pred)

pred_samples = np.array(pred_samples)

# Calcular estatísticas
mean_scientific = pred_samples.mean(axis=0)
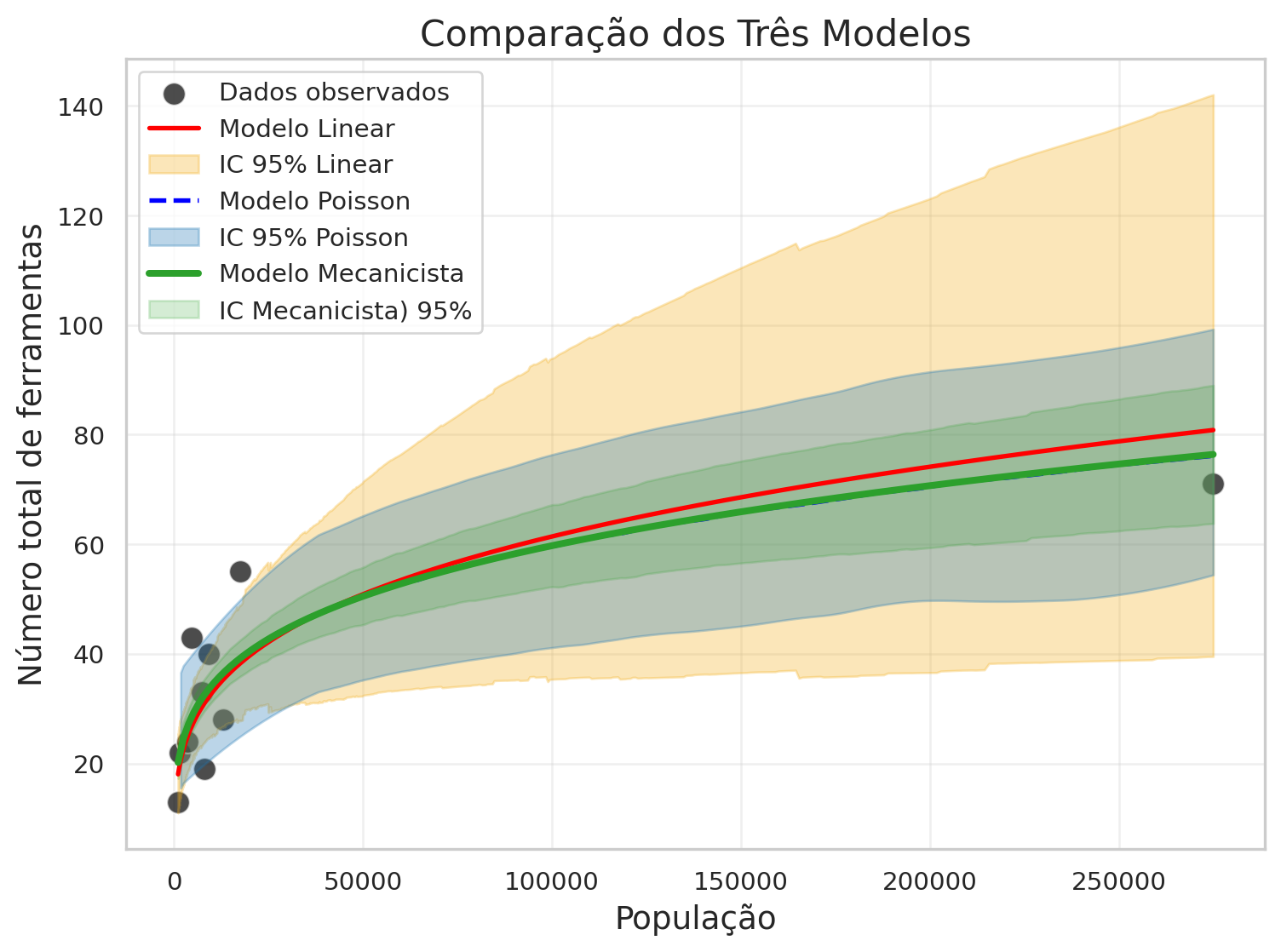
hdi_scientific = az.hdi(pred_samples, hdi_prob=0.89)

5 Comparação dos Três Modelos

Vamos comparar as predições dos três modelos em um único gráfico:

plt.figure(figsize=(8, 6))

# Dados observados (plotados apenas uma vez)
sns.scatterplot(data=kline, x='population', y='total_tools', 
                s=100, alpha=0.7, color='black', label='Dados observados')

# 1. Modelo Linear com transformação log (escala original)
plt.plot(np.exp(new_x), np.exp(new_pred_linear_mean), 
         color='red', linewidth=2, label='Modelo Linear')
plt.fill_between(np.exp(new_x),
                 ic_linear.sel(hdi='lower')['x'],
                 ic_linear.sel(hdi='higher')['x'],
                 alpha=0.3, color='#f3ae1a', 
                 label='IC 95% Linear')

# 2. Modelo Poisson (GLM)
plt.plot(np.exp(log_pop_new), new_pred_poisson_mean.values, 
         color='blue', linewidth=2, linestyle='--', label='Modelo Poisson')
az.plot_hdi(
    np.exp(log_pop_new),
    new_pred_poisson.posterior_predictive.total_tools,
    hdi_prob=0.95,
    color='#1f77b4',
    fill_kwargs={'alpha': 0.3, 'label': 'IC 95% Poisson'},
)

# 3. Modelo Científico (Mecanicista)
# Modelo Científico
plt.plot(pop_pred, mean_scientific, color='#2ca02c', linewidth=3, 
         label='Modelo Mecanicista')
plt.fill_between(pop_pred, hdi_scientific[:, 0], hdi_scientific[:, 1],
                 color='#2ca02c', alpha=0.2, label = 'IC Mecanicista) 95%')

# Configurações do gráfico
plt.xlabel('População', fontsize=14)
plt.ylabel('Número total de ferramentas', fontsize=14)
plt.title('Comparação dos Três Modelos', fontsize=16)
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()

Referências

Kline, Michelle A, e Robert Boyd. 2010. «Population size predicts technological complexity in Oceania». Proceedings of the Royal Society B: Biological Sciences 277 (1693): 2559–64. https://www.researchgate.net/publication/43147721_Population_Size_Predicts_Technological_Complexity_in_Oceania.

McElreath, Richard. 2018. Statistical rethinking: A Bayesian course with examples in R and Stan. Chapman; Hall/CRC.