Explorando Modelos de Regressão Bayesiana

Dos modelos lineares a respostas generalizadas e estruturas hierárquicas

Prof. Fabio Cop

Laboratório de Ecologia e Dinâmica de Comunidades (LaEDCom)

O que aprendemos até aqui: prioris e posterioris

O que aprendemos até aqui: distribuição Normal de Probabilidade

\[ f(y) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{1}{2} \left(\frac{y - \mu}{\sigma} \right)^2} \longrightarrow \quad y \sim \mathcal{N}(\mu, \sigma) \]

O que aprendemos até aqui: o modelo de Regressão linear

---

Variável aleatória resposta

---

\[ y \sim \mathcal{N}(\mu, \sigma) \]

\[ \mu = \beta_0 + \beta_1 x \]

---

Prioris

---

\[ \beta_0 \sim \mathcal{N}(\mu_{\beta_0}, \sigma_{\beta_0}) \]

\[ \beta_1 \sim \mathcal{N}(\mu_{\beta_1}, \sigma_{\beta_1}) \]

\[ \sigma \sim \text{Lognormal}(\mu_{\log \sigma}, \sigma_{\log \sigma}) \]

O que aprendemos até aqui: Programação Probabilística

---

PyMC

---

with pm.Model() as modelo:
    # Definição das prioris
    Intercept = pm.Normal("Intercept", mu=60, sigma=5)
    calcado = pm.Normal("calcado", mu=2.8, sigma=0.1)
    sigma = pm.HalfNormal("sigma", sigma=10)
    
    # Definição do modelo
    mu = beta_0 + beta_1 * X
    altura = pm.Normal("altura", mu=mu, sigma=sigma, 
                        observed=Y)
    
    # Amostra a distribuição posterior
    resultados = pm.sample()

---

Bambi

---

# Definição das prioris
custom_priors = {
    "Intercept": bmb.Prior("Normal", mu=60, sigma=5),
    "calcado": bmb.Prior("Normal", mu=2.8, sigma=0.1),
    "sigma": bmb.Prior("HalfNormal", sigma=10)
}

# Definição do modelo
modelo = bmb.Model("altura ~ calcado", df, 
                    priors=custom_priors)

# Amostra a distribuição posterior
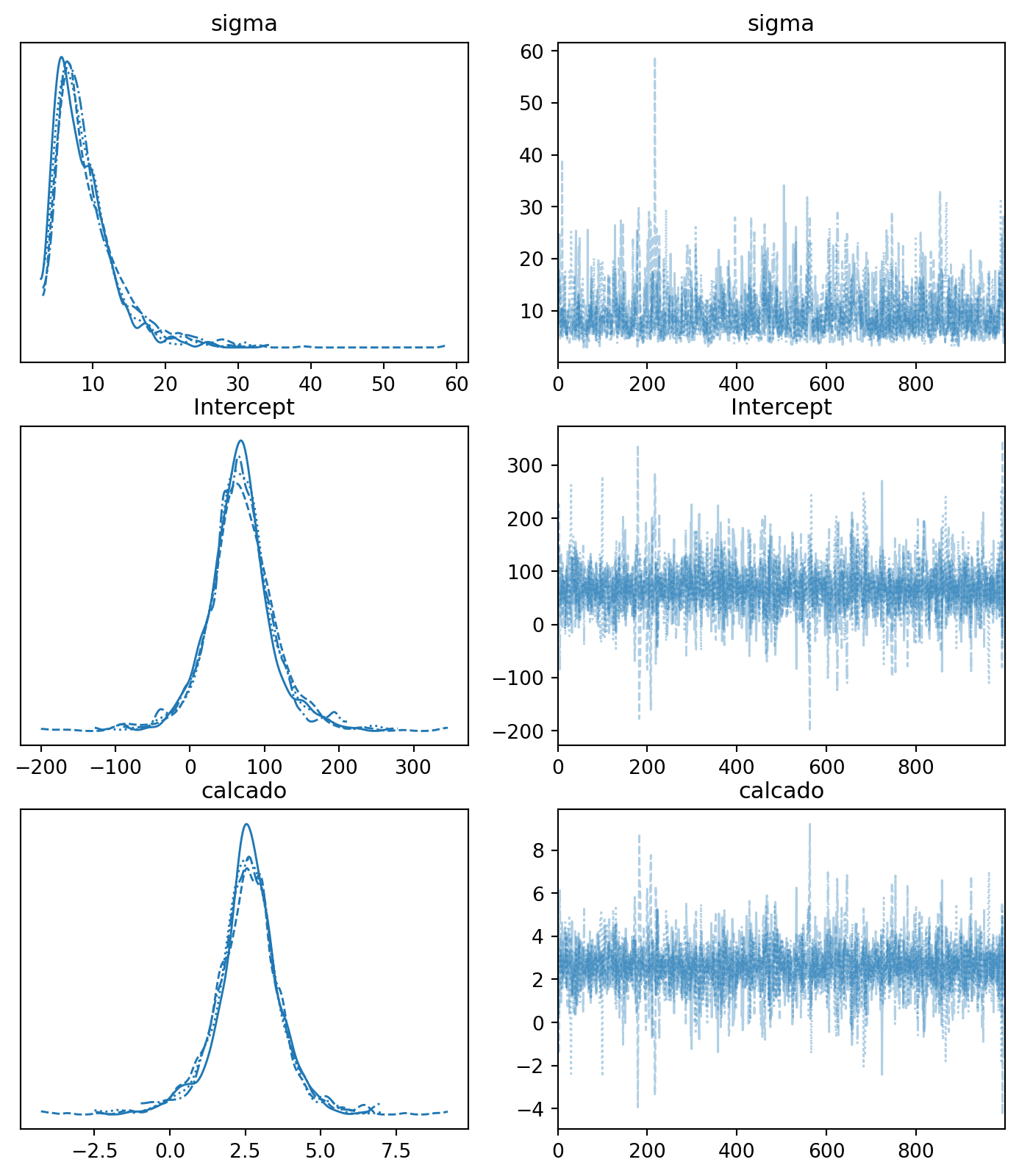
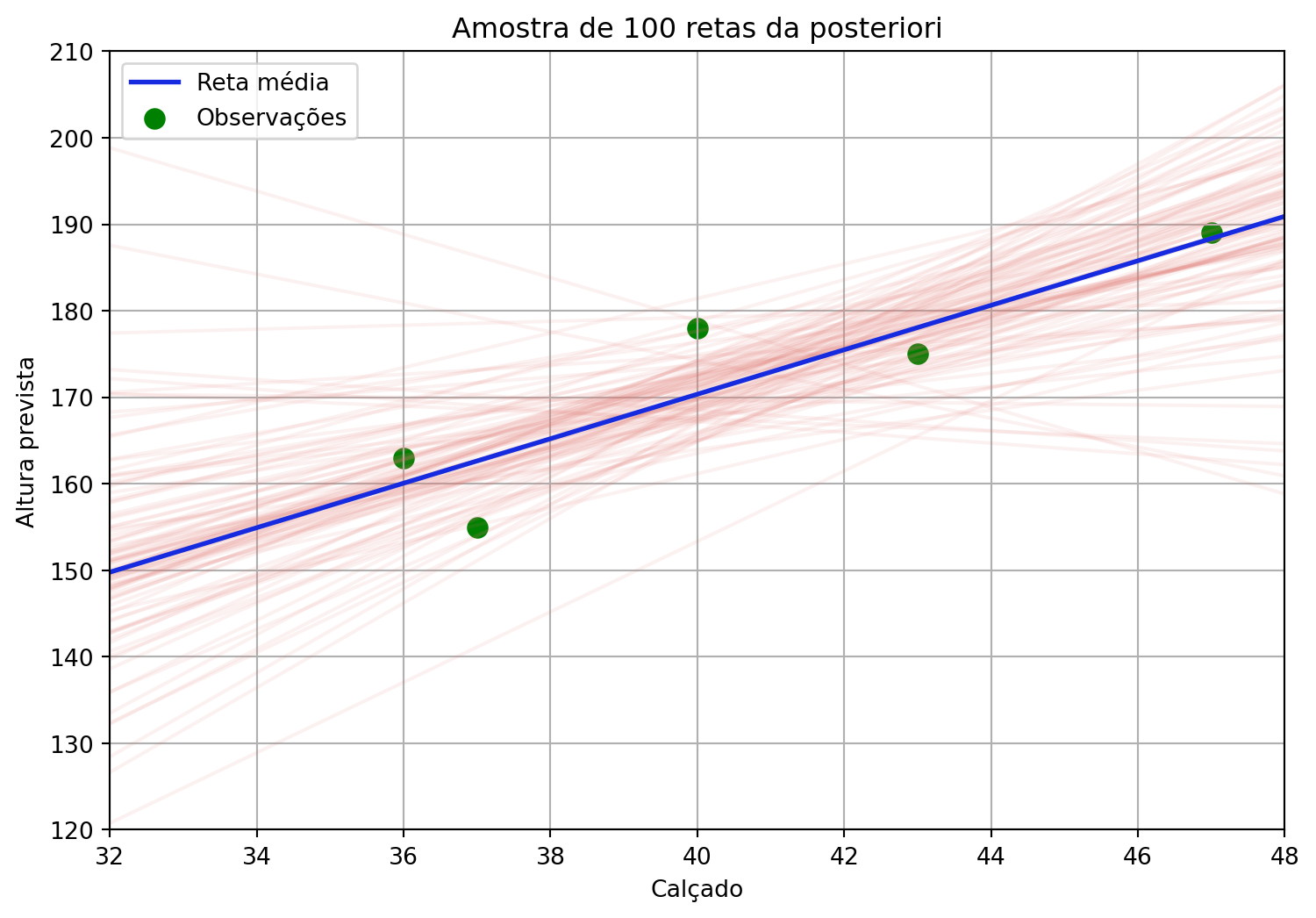
resultados = modelo.fit()

O que aprendemos até aqui: ajuste da posteriori

Daqui para frente: uma variedade de modelos e estruturas

1. Extenção da Regressão Linear para:
   • Múltiplos preditores.
   • Diferentes tipos de variáveis resposta (GLMs).
   • Dados com estrutura de agrupamento (Modelos Hierárquicos).

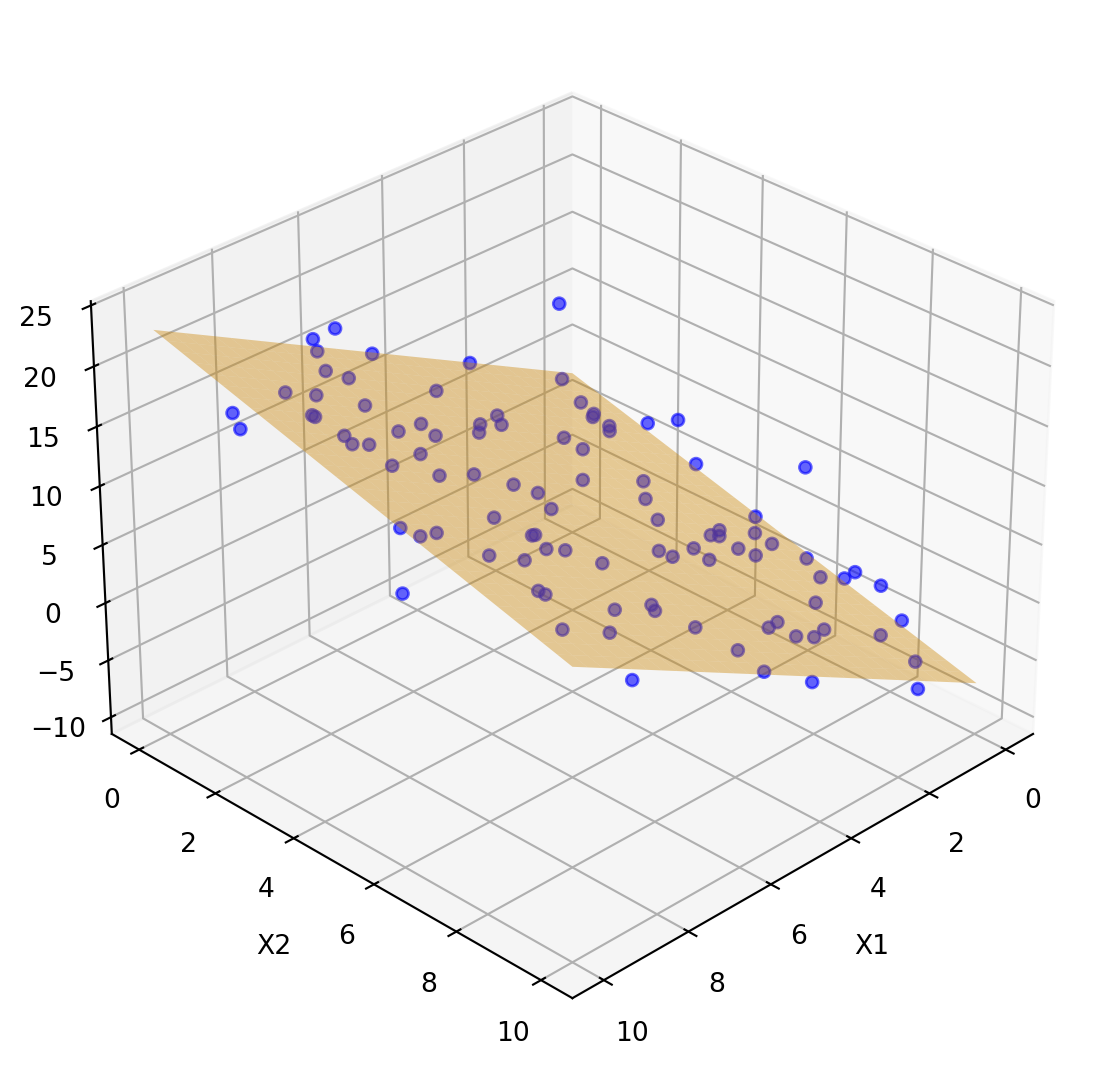
Regressão linear múltipla

---

Variável aleatória resposta

---

\[ y \sim \mathcal{N}(\mu, \sigma) \]

\[ \mu = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_k x_k \]

---

Prioris

---

\[ \beta_0 \sim \mathcal{N}(\mu_{\beta_0}, \sigma_{\beta_0}) \]

\[ \beta_j \sim \mathcal{N}(\mu_{\beta_j}, \sigma_{\beta_j}) \quad \text{para } j = 1, \dots, k \]

\[ \sigma \sim \text{Lognormal}(\mu_{\log \sigma}, \sigma_{\log \sigma}) \]

Programação Probabilística

---

PyMC

---

with pm.Model() as modelo:
    # Definição das prioris
    Intercept = pm.Normal("Intercept", mu=60, sigma=5)
    beta_1 = pm.Normal("beta_1", mu=2.8, sigma=0.1)
    beta_2 = pm.Normal("beta_2", mu=1.5, sigma=0.1)
    sigma = pm.HalfNormal("sigma", sigma=10)

    # Definição do modelo
    mu = Intercept + beta_1 * X1 + beta_2 * X2
    altura = pm.Normal("altura", mu=mu, sigma=sigma, 
                       observed=Y)

    # Amostra a distribuição posterior
    resultados = pm.sample()

---

Bambi

---

# Definição das prioris
custom_priors = {
    "Intercept": bmb.Prior("Normal", mu=60, sigma=5),
    "X1": bmb.Prior("Normal", mu=2.8, sigma=0.1),
    "X2": bmb.Prior("Normal", mu=1.5, sigma=0.1),
    "sigma": bmb.Prior("HalfNormal", sigma=10)
}

# Definição do modelo
modelo = bmb.Model("altura ~ X1 + X2", df, 
                   priors=custom_priors)

# Amostra a distribuição posterior
resultados = modelo.fit()

Regressão de Poisson: dados de contagem

\[ y \sim \text{Poisson}(\lambda) \]

\[ \log(\lambda) = \mu = \beta_0 + \beta_1 x \]

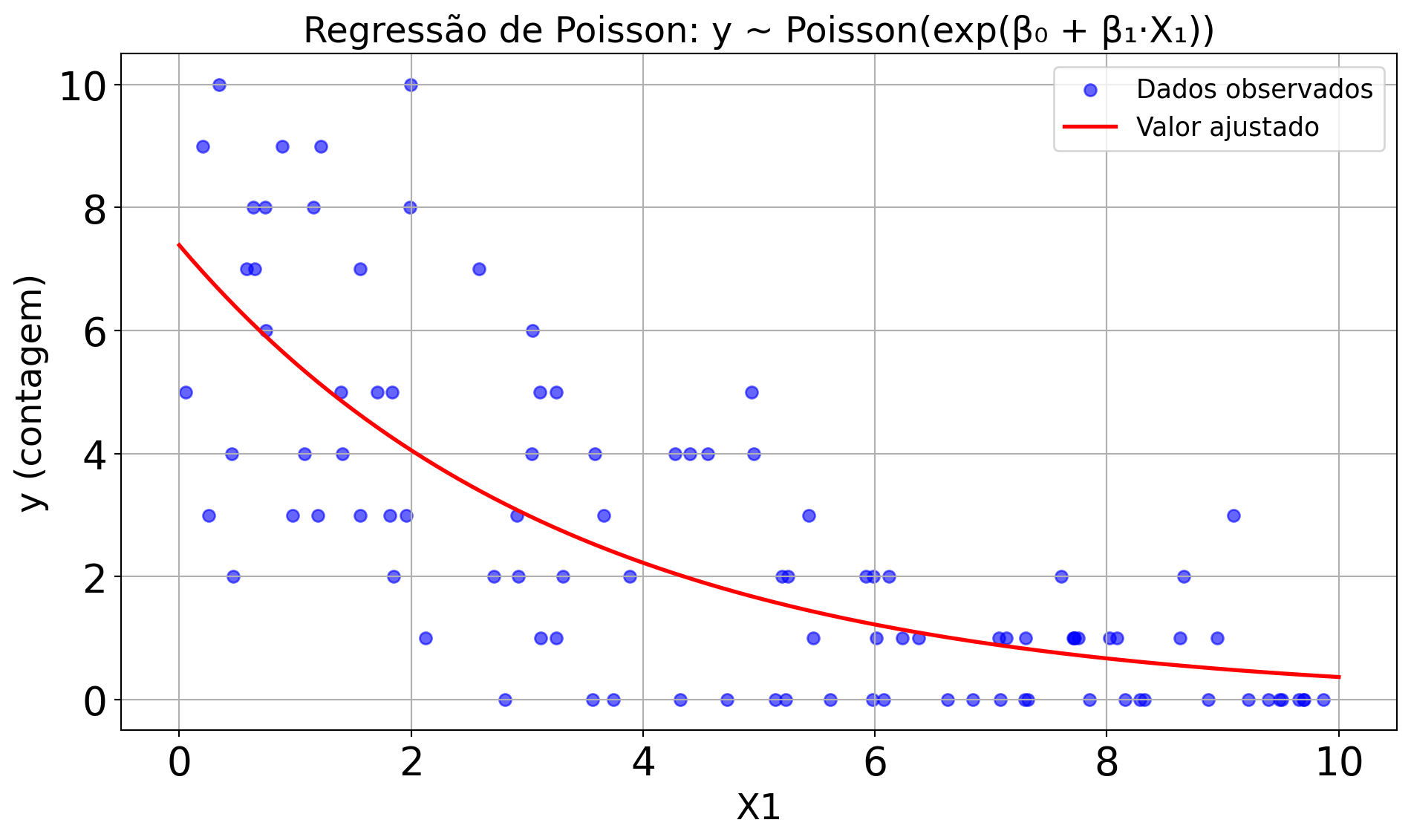
Regressão de Poisson: dados de contagem

\[ f(y) = \frac{e^{-\lambda} \lambda^y}{y!} \longrightarrow \quad y \sim \text{Poisson}(\lambda) \]

\[ \log(\lambda) = \mu \]

---

Variável aleatória resposta

---

\[ y \sim \text{Poisson}(\lambda) \]

\[ \log(\lambda) = \mu = \beta_0 + \beta_1 x \]

---

Prioris

---

\[ \beta_0 \sim \mathcal{N}(\mu_{\beta_0}, \sigma_{\beta_0}) \]

\[ \beta_1 \sim \mathcal{N}(\mu_{\beta_1}, \sigma_{\beta_1}) \]

Programação Probabilística

---

PyMC

---

with pm.Model() as modelo:
    # Definição das prioris
    Intercept = pm.Normal("Intercept", mu=0, sigma=5)
    beta = pm.Normal("beta", mu=0, sigma=2)
    
    # Função de ligação log: log(λ) = μ = Intercept + beta * X
    mu = Intercept + beta * X
    lambda_ = pm.math.exp(mu)
    
    # Modelo de verossimilhança
    contagem = pm.Poisson("contagem", mu=lambda_, 
                          observed=Y)
    
    # Amostragem
    resultados = pm.sample()

---

Bambi

---

# Definição das prioris
custom_priors = {
    "Intercept": bmb.Prior("Normal", mu=0, sigma=5),
    "x": bmb.Prior("Normal", mu=0, sigma=2),
}

# Modelo com função de ligação log (default da família Poisson)
modelo = bmb.Model("contagem ~ x", df, 
                   family="poisson", priors=custom_priors)

# Amostragem
resultados = modelo.fit()

Regressão Logística: dados dicotômicos

\[ y \sim \text{Bernoulli}(p) \]

\[ \log\left(\frac{p}{1-p}\right) = \mu = \beta_0 + \beta_1 x \]

\[ p = \frac{e^{\beta_0 + \beta_1 x}}{1 + e^{\beta_0 + \beta_1 x}} \]

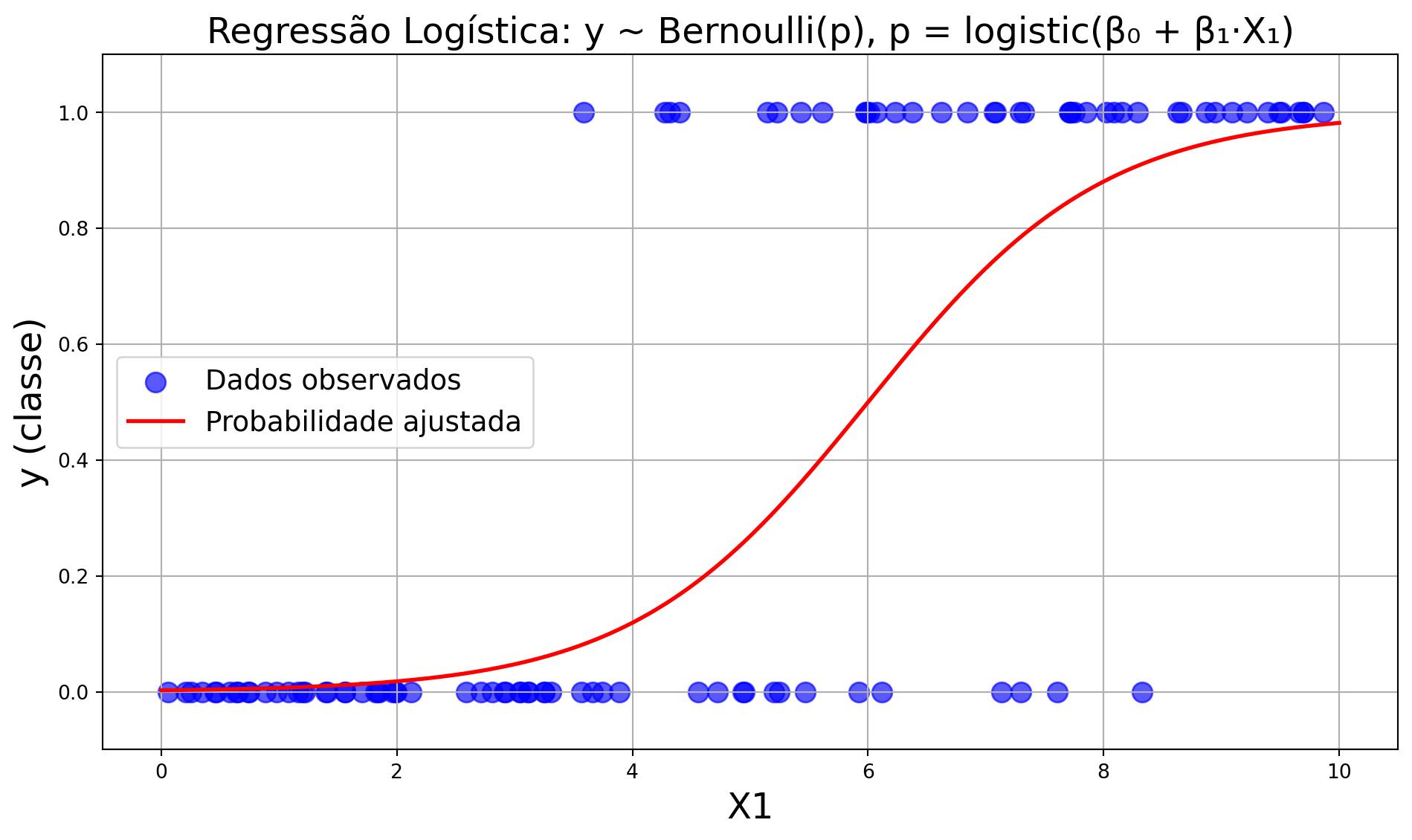
Regressão Logística: dados dicotômicos

---

Distribuição da variável resposta

---

\[ f(y) = p^y (1 - p)^{1 - y} \]

\[ y \sim \text{Bernoulli}(p) \]

---

Função de ligação

---

\[ \text{logit}(p) = \mu = \beta_0 + \beta_1 x \]

\[ \text{logit}(p) = \log\left(\frac{p}{1 - p}\right) \]

\[ \log\left(\frac{p}{1 - p}\right) = \beta_0 + \beta_1 x \]

\[ \frac{p}{1 - p} = e^{\beta_0 + \beta_1 x} \]

\[ p = (1 - p) \cdot e^{\beta_0 + \beta_1 x} \]

\[ p = e^{\beta_0 + \beta_1 x} - p \cdot e^{\beta_0 + \beta_1 x} \]

\[ p \left(1 + e^{\beta_0 + \beta_1 x}\right) = e^{\beta_0 + \beta_1 x} \]

\[ p = \frac{e^{\beta_0 + \beta_1 x}}{1 + e^{\beta_0 + \beta_1 x}} = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x)}} \]

Programação Probabilística

---

PyMC

---

with pm.Model() as modelo:
    # Definição das prioris
    Intercept = pm.Normal("Intercept", mu=0, sigma=5)
    beta = pm.Normal("beta", mu=0, sigma=2)
    
    # Preditor linear e função de ligação logit
    mu = Intercept + beta * X
    p = pm.math.sigmoid(mu)
    
    # Verossimilhança
    y_obs = pm.Bernoulli("y_obs", p=p, observed=Y)
    
    # Amostragem
    resultados = pm.sample()

---

Bambi

---

# Definição das prioris
custom_priors = {
    "Intercept": bmb.Prior("Normal", mu=0, sigma=5),
    "x": bmb.Prior("Normal", mu=0, sigma=2),
}

# Modelo logístico (ligação logit é padrão para bernoulli)
modelo = bmb.Model("y ~ x", df, 
                   family="bernoulli", priors=custom_priors)

# Amostragem
resultados = modelo.fit()

Modelo Hierárquico Normal com Intercepto e Inclinação Variáveis

\[ y_{ij} \sim \mathcal{N}(\mu_{ij}, \sigma^2) \]

\[ \mu_{ij} = \beta_{0j} + \beta_{1j} x_{ij} \]

\[ \beta_{0j} \sim \mathcal{N}(\gamma_0, \tau_0^2) \\ \beta_{1j} \sim \mathcal{N}(\gamma_1, \tau_1^2) \]

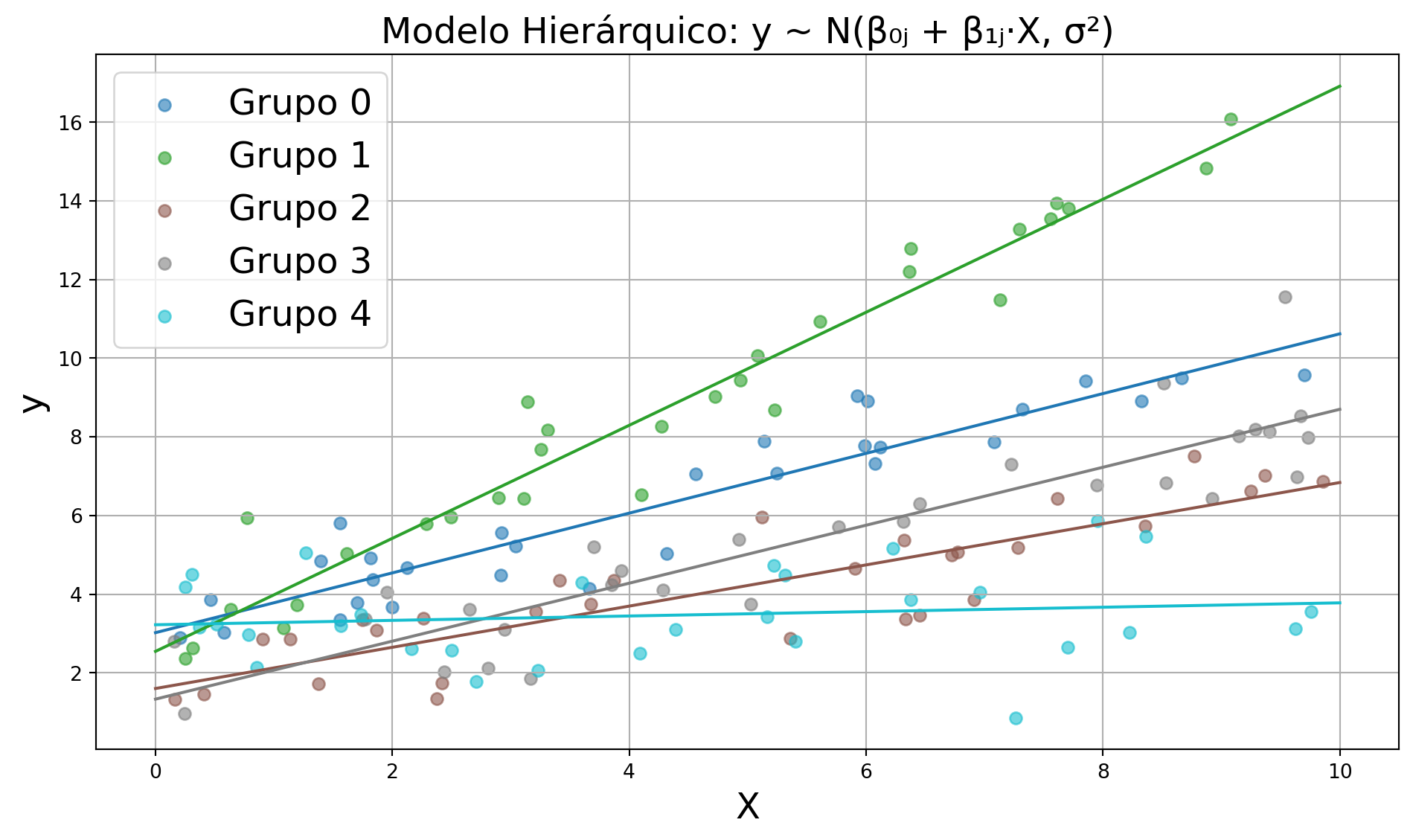
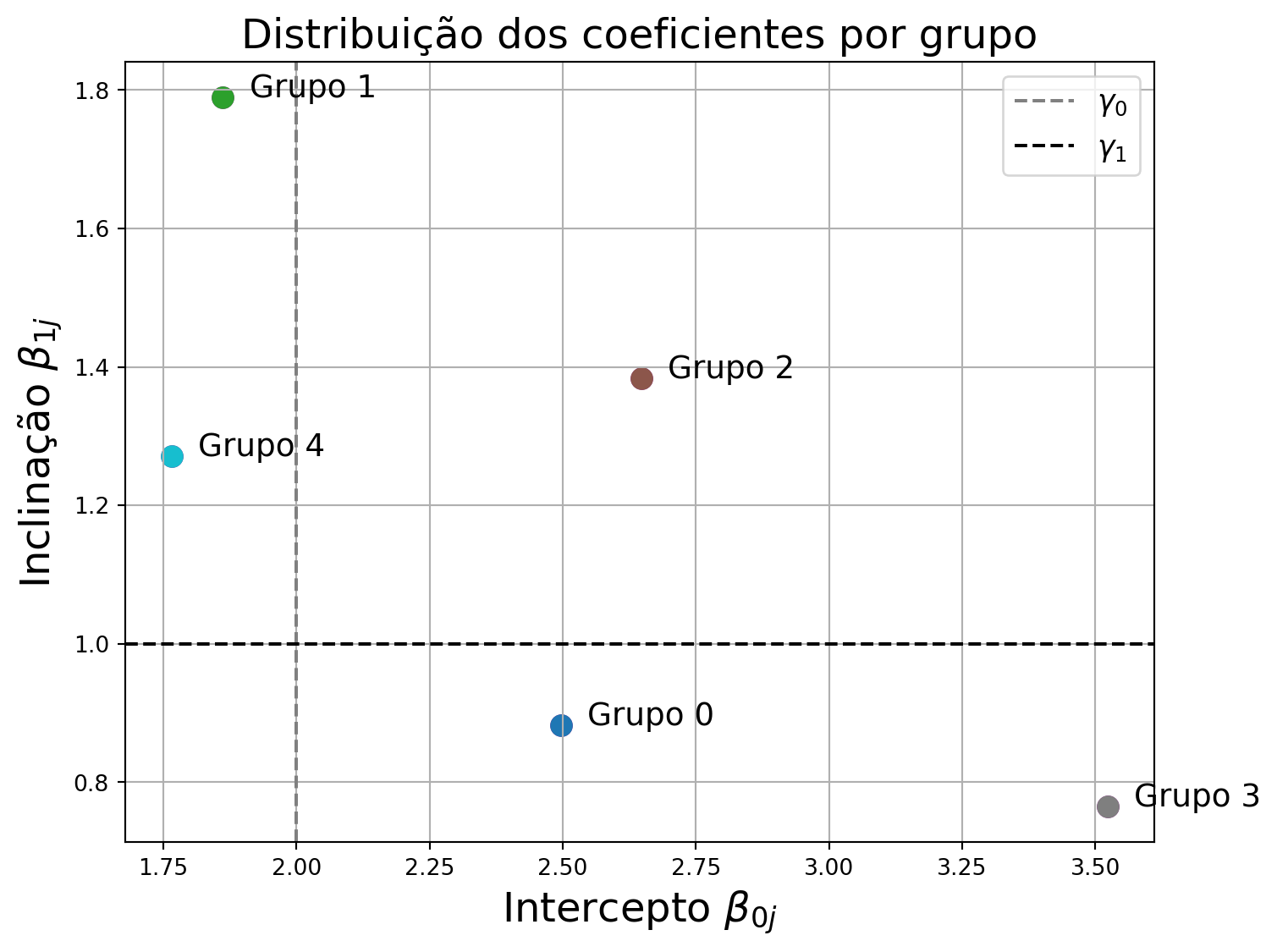
Variação entre grupos: coeficientes do modelo hierárquico

Coeficientes específicos por grupo:

\[ \beta_{0j} \sim \mathcal{N}(\gamma_0, \tau_0^2) \\ \beta_{1j} \sim \mathcal{N}(\gamma_1, \tau_1^2) \]

Visualizando a dispersão dos parâmetros em relação às médias populacionais \(\gamma_0, \gamma_1\).