Associação entre duas variáveis qualitativas

Estatística

Análise qualitativa

Tabelas de contingência

Medidas de associação

Análise da associação entre variáveis qualitativas, uso de tabelas de contingência e estatísticas de associação.

Pacotes e funções utilizadas no capítulo

library(tidyverse)
library(gt)
library(patchwork)
library(gridExtra)
source('scripts/assoc_municipies.r')

Imagine que haverá uma obra de revitalização de uma área na região central da cidade. A obra implicará na melhoria de acesso, de segurança e na oferta de serviços. Entretanto como levará tempo para ser concluída, haverá ações de remoção de moradias irregulares, interdição de ruas e avenidas por longos períodos, etc. A prefeitura encomenda uma pesquisa para saber a opinião dos munícipes. A cada entrevistado são feitas duas perguntas:

Qual sua opinião sobre a necessidade de realização da obra?

A favor
Contra

Você reside na região diretamente afetada:

Residente
Não-Residente

A base de dados completa está disponível em datasets

Com estas entrevistas desejamos responder à seguinte questão:

Questão do capítulo

Moradores Residentes da região central têm uma opinião consistentemente diferente de moradores Não-residentes no que se refere a ser A favor ou Contra a obra?

Importe a base de dados

mun = read_delim('https://raw.githubusercontent.com/FCopf/datasets/refs/heads/main/Entrevista_municipes.csv',
                  delim = ',')

n_amostra = 12
n = nrow(mun)  # Número de entrevistados

Após entrevistar 200 pessoas selecionadas ao acaso de uma lista da moradores da cidade, foi construída uma tabela com três colunas: Entrevistado (sequência numérica do primeiro ao último respondente), Opinião e Moradia.

Veja os primeiros 12 resultados das entrevistas:

Tabela 1: Respostas dos primeiros munícipies entrevistados.

Entrevistado	Opiniao	Moradia
1	A favor	Residente
2	A favor	Residente
3	A favor	Residente
4	A favor	Residente
5	Contra	Não-Residente
6	Contra	Residente
7	A favor	Não-Residente
8	Contra	Não-Residente
9	A favor	Não-Residente
10	A favor	Não-Residente
11	A favor	Residente
12	A favor	Não-Residente

Estão descritos na Tabela 1 os resultados das primeiras 12 entrevistas, onde é possível ver ao menos uma combinação de todas as possíveis respostas. O entrevistado pode ser:

A favor e ser Residente da região;
A favor e ser Não-Residente;
Contra e ser Residente;
Contra e ser Não-Residente.

1 Tabelas de frequência e gráficos de barras

Inicialmente, vamos representar cada uma das variáveis por meio de uma tabela de frequência dos 200 entrevistados.

Código

resumo_opiniao = mun |> 
  group_by(Opiniao) |> 
  summarise(Op_n = n()) |> 
  mutate(Op_rel = Op_n/sum(Op_n))

resumo_opiniao |> 
  gt()

Opiniao	Op_n	Op_rel
A favor	144	0.72
Contra	56	0.28

Das $200$ respostas tivemos $144$ pessoas A favor ($72\%$) e $56$ pessoas Contra ($28\%$).

Código

resumo_opiniao = mun |> 
  group_by(Opiniao) |> 
  summarise(Op_n = n()) |> 
  mutate(Op_rel = Op_n/sum(Op_n))

resumo_opiniao |> 
  gt()

Opiniao	Op_n	Op_rel
A favor	144	0.72
Contra	56	0.28

Com relação ao local de residência:

Código

resumo_morad = mun |> 
  group_by(Moradia) |> 
  summarise(Morad_n = n()) |> 
  mutate(Morad_rel = Morad_n/sum(Morad_n))

resumo_morad |> 
  gt()

Moradia	Morad_n	Morad_rel
Não-Residente	117	0.585
Residente	83	0.415

Responderam à entrevistas um total de $117$ pessoas Não-Residente ($58.5\%$) e $83$ pessoas Residente ($41.5\%$)

Se visualizarmos estes totais em gráficos de barras individuais teremos:

Código

plt_op = ggplot(mun, aes(x = Opiniao)) +
  geom_bar(fill = 'darkblue', color = 'white') +
  coord_cartesian(ylim = c(0, 150)) +
  labs(y = 'Número de respostas') +
  theme_classic(base_size = 15)

plt_morad = ggplot(mun, aes(x = Moradia)) +
  geom_bar(fill = 'darkred', color = 'white') +
  coord_cartesian(ylim = c(0, 150)) +
  labs(y = 'Número de respostas') +
  theme_classic(base_size = 15)

plt_op + plt_morad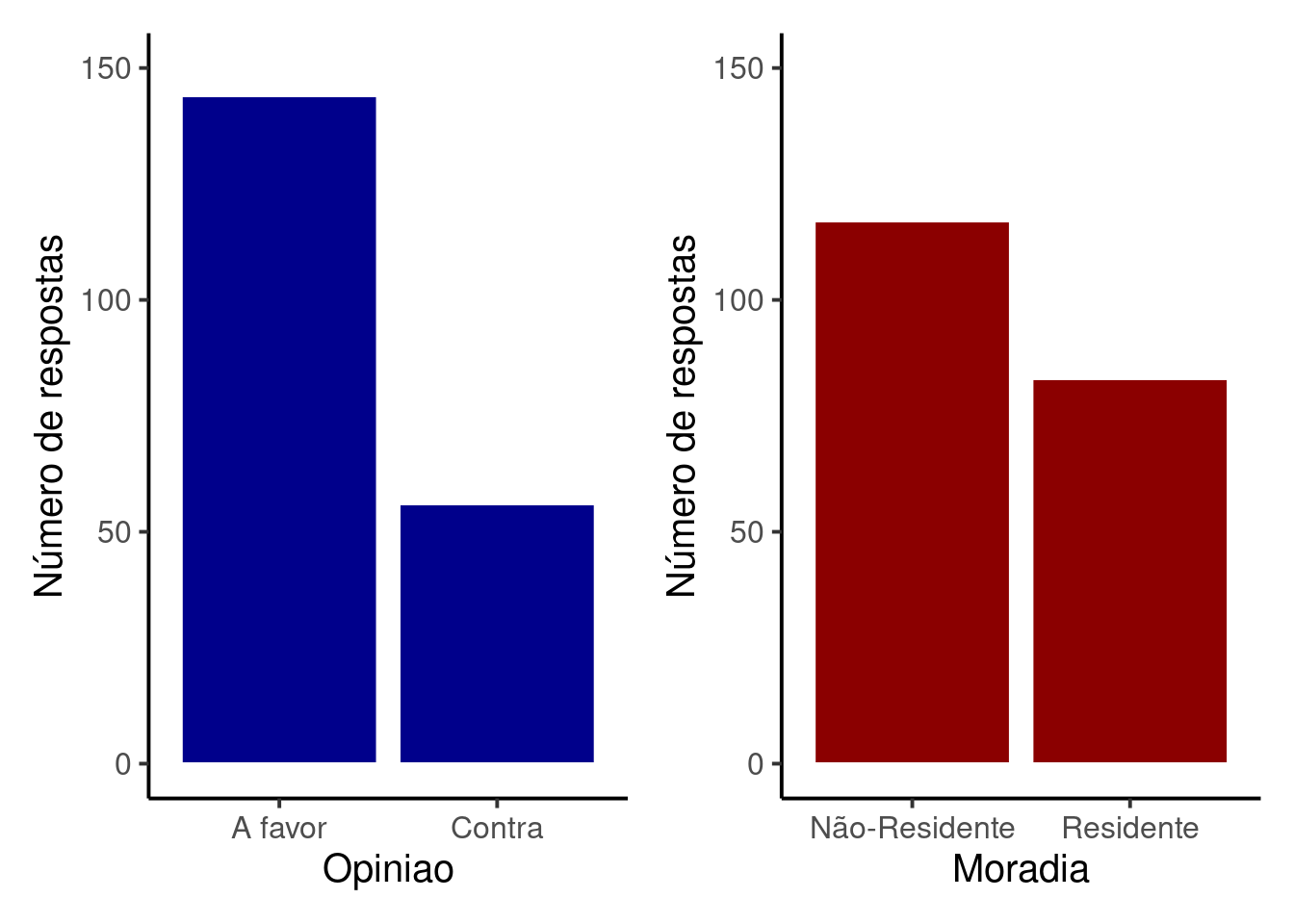

Figura 1: Respostas dos munícipies entrevistados para cada questão separadamente.

Existe portanto um predomínio de pessoas A Favor e um ligeiro predomínio de entrevistados Não-Residentes.

Para responder à questão do capítulo, precisamos verificar se existe alguma associação entre as respostas dadas às duas perguntas explorando a distribuição conjunta dos totais respondidos.

2 Tabelas de contingência

Tabelas de contigência são organizadas para verificarmos a associação entre duas variáveis qualitativas. São conhecidas também como tabelas de dupla entrada. Nas colunas estão os níveis da variável $X$ e nas linhas os níveis da variável $Y$.

Para nosso exemplo, podemos fazer simplesmente:

tcont = table(mun$Opiniao, mun$Moradia)
tcont

         
          Não-Residente Residente
  A favor            81        63
  Contra             36        20

Temos:

81 - A favor e Não-Residente;
63 - A favor e Residente;
36 - Contra e Não-Residente;
20 - Contra e Residente

Podemos ver os totais marginais das linhas:

tcont_linhas = apply(tcont, 1, sum)
tcont_linhas

A favor  Contra 
    144      56

Ou os totais marginais das colunas:

tcont_colunas = apply(tcont, 2, sum)
tcont_colunas

Não-Residente     Residente 
          117            83

Que são justamente os totais que verificamos nas distribuições individuais.

Se quisermos ver as frequências relativas marginais podemos fazer:

trel_linha = prop.table(tcont, 1)
trel_linha

         
          Não-Residente Residente
  A favor     0.5625000 0.4375000
  Contra      0.6428571 0.3571429

Neste caso estamos vendo as frequências relativas das linhas, isto é, cada linha nesta tabela soma $1$. O que vemos nesta tabela é que:

dos $144$ entrevistados que são A favor, cerca de $56.25\%$ são Não-Residente, enquanto os demais $43.75\%$ são Residente
dos $56$ entrevistados que são Contra, cerca de $64.29\%$ são Não-Residente, enquanto os demais $35.71\%$ são Residente

Podemos fazer exatamente o mesmo olhando para as frequências marginais por colunas:

trel_coluna = prop.table(tcont, 2)
trel_coluna

         
          Não-Residente Residente
  A favor     0.6923077 0.7590361
  Contra      0.3076923 0.2409639

Neste caso são as colunas que somam $1$, portanto:

dos $117$ entrevistados que são Não-Residente, cerca de $69.23\%$ são A favor, enquanto os demais $30.77\%$ são Contra
dos $83$ entrevistados que são Residente, cerca de $75.9\%$ são A favor, enquanto os demais $75.9\%$ são Contra

Podemos finalmente ver a frequência relativa conjunta:

trel_conjunta = prop.table(tcont)
trel_conjunta

         
          Não-Residente Residente
  A favor         0.405     0.315
  Contra          0.180     0.100

Em que o somatório das linhas é igual a:

tcont_linhas / sum(tcont_linhas)

A favor  Contra 
   0.72    0.28

indicando os valores relativos das opiniões A Favor e Contra.

O somatório das colunas é igual a:

tcont_colunas / sum(tcont_colunas)

Não-Residente     Residente 
        0.585         0.415

indicando os valores relativos de Não-Residentes e Residentes.

Na tabela de frequência relativa conjunta, o somatório total da tabela deve ser igual a $1$.

3 O gráfico de barras para duas variáveis qualitativas

Existem várias formas de gerar um gráfico de barras combinando as duas variáveis. Se quisermos utilizar a própria tabela de contingência obtida a partir do comando table(mun$Opiniao, mun$Moradia), podemos utilizar o comando barplot(). Por outro lado, se quisermos utilizar a tabela original de dados (objeto mun) podemos fazer uso do pacote ggplot2:

Código

plt_bar1 = ggplot(mun) +
  aes(x = Moradia, fill = Opiniao) +
  geom_bar(color = 'white', position = 'dodge') +
  scale_fill_manual(values = c('Contra' = 'darkred',
                               'A favor' = 'darkblue')) +
  coord_cartesian(ylim = c(0, 80)) +
  labs(y = 'Número de respostas') +
  theme_classic(base_size = 15)

plt_bar1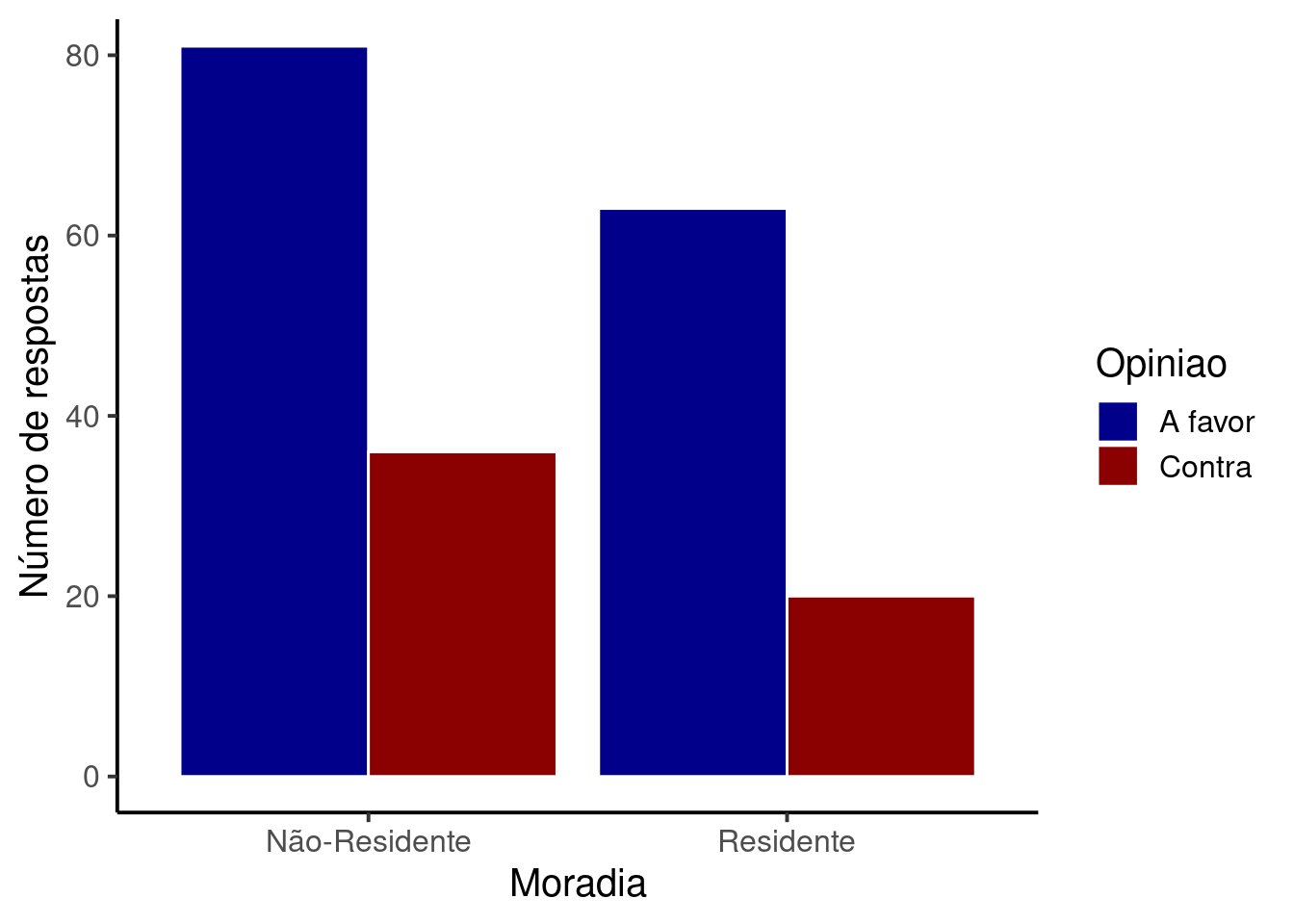

Figura 2: Respostas dos munícipies entrevistados combinando local de moradia e opinião.

Veja que nesta figura, existem mais opiniões A favor, independente do entrevistado ser ou não residente da região central. Este padrão é o mesmo que observamos no gráfico da variável Opinião isoladamente, o que sugere não haver associação entre as variáveis Opinião e Moradia. Ao que parece, a opinião de um entrevistado sobre a construção da obra não depende de seu local de moradia.

Exemplos de associações entre duas variáveis

Abaixo são apresentadas quatro situações em que existe associação Opinião e Moradia.

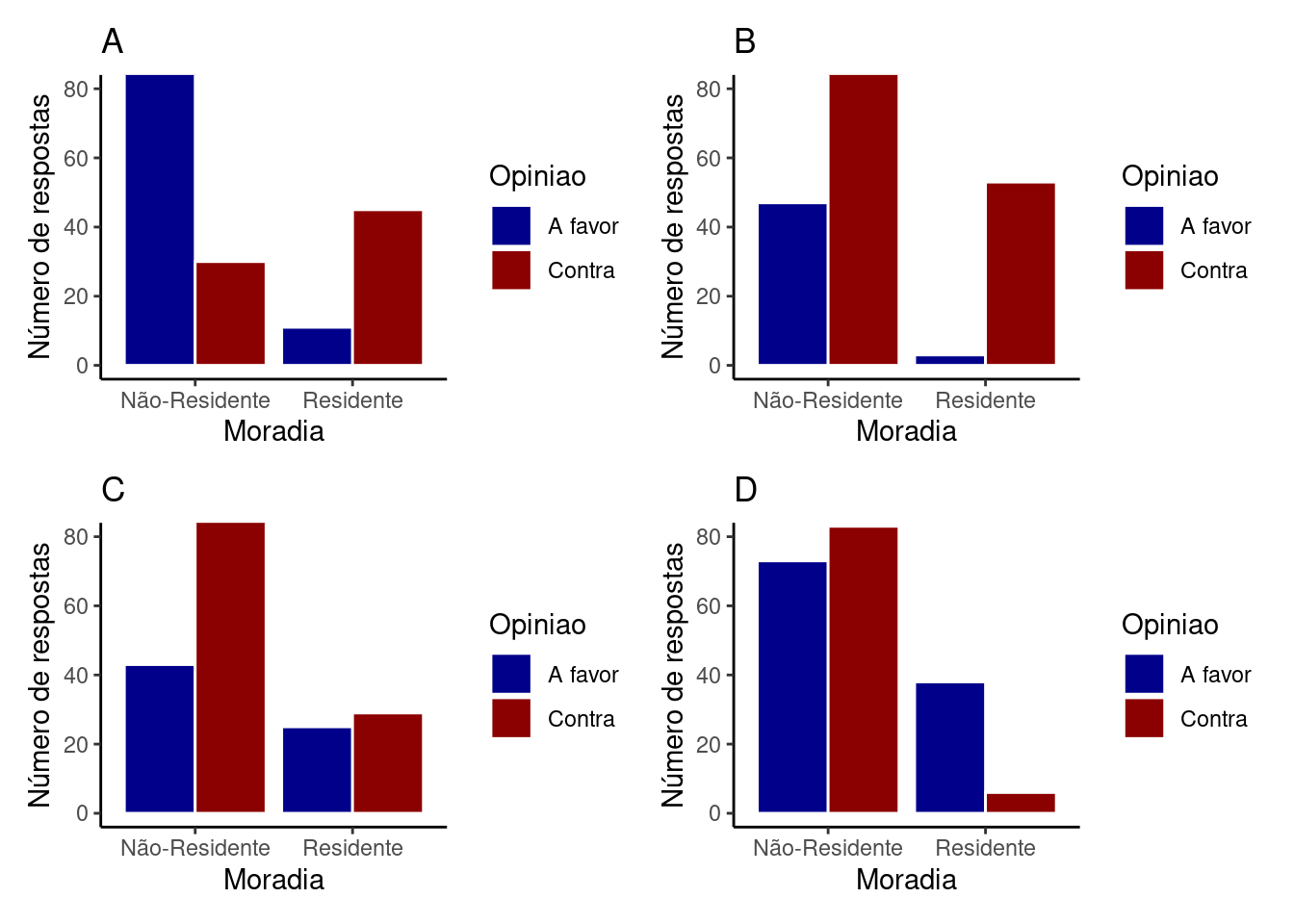
Em todos estes exemplos, note que a relação as opiniões A favor ou Contra dependem se o entrevistado é ou não Residente na região. Esses padrões configuram diferentes tipos de associação entre as variáveis Opinião e Moradia, a saber:

Figura A: Não-Residentes tendem a ser A favor e Residentes são em sua maioria Contra;
Figura B: todos tendem a ser Contra, mas a diferença de opiniões é maior entre os Residentes;
Figura C: Não-Residentes tendem a ser Contra, enquanto não parece haver diferenças entre os Residentes;
Figura D: Residentes tendem a ser A favor, enquanto não parece haver diferenças entre os Residentes;

4 Medindo a discrepância com o índice de $\chi^2$ de Pearson

O índice de qui-quadrado ($\chi^2$) mede a discrepância entre os valores observados e os valores esperados em uma tabela de contingência.

Digamos que um município tenha $20\%$ de sua população morando em área Rural e os outros $80\%$ em área Urbana. Se fizermos uma amostragem ao acaso dos moradores é esperado que esta frequência relativa se reflita na amostra. Neste caso se sorteamos $200$ pessoas, seria esperado:

Zona Rural: $40$ moradores
Zona Urbana $160$ moradores

Entretando, se fazemos um sorteio ao acaso, haverá alguma variação ao redor destes valores, de modo que as frequências observadas ($o$) deverão ser diferentes das esperadas ($e$). O $\chi^2$ mede a discrepância entre $o$ e $e$ para cada célula de uma tabela de contigência como:

\[\chi^2 = \sum_{i=1}^{n}\frac{(o_i - e_i)^2}{e_i}\] Para uma tabela de frequências, devemos determinar portanto os valores de $o_i$ e $e_i$.

Suponha que uma amostra de $200$ moradores tenha resultado em:

Código

set.seed(10)
nor = sum(rbinom(n = n, size = 1, prob = pr))
Moradia_obs = data.frame(Regiao = c(rep('Rural', nor),
                           rep('Urbana', n - nor)))

tb_dfo = table(Moradia_obs)
tb_dfo

Regiao
 Rural Urbana 
    31    169

As frequências observadas e esperadas serão:

Zona Rural:

$o_{Rural} = 31$

$e_{Rural} = 0.2 \times 200 = 40$

Zona Urbana

$o_{Urbana} = 169$

$e_{Urbana} = 0.8 \times 200 = 160$

De modo que o valor de $\chi^2$ será:

$\chi^2 = \frac{(31 - 40)^2}{40} + \frac{(169 - 160)^2}{160} = \frac{(-9)^2}{40} + \frac{(9)^2}{160} = 2.025 + 0.50625 = 2.53125$

5 O índice de $\chi^2$ em uma tabela de contigência

No exemplo acima, as contagens esperadas foram definidas a partir de um modelo que dizia que as populações rurais e urbanas se dividiam nas proporções $20\%:80\%$. Em uma tabela de contigência, a hipótese em verificação é a de que não há associação entre $X$ e $Y$. Se for assim, é esperado que as frequências conjuntas sejam porporcionais às frequências marginais. Vamos apresentar esta ideia utilizando uma notação geral para tabelas de contingência e, em seguida, discutir com um exemplo.

A tabela Tabela 2 apresenta $r$ linhas por $s$ colunas com as contagens de todas as combinações dos níveis da variável $X$ (Níveis $A_{1}$ a $A_{r}$) e da variável $Y$ (Níveis $B_{1}$ a $B_{s}$). Os totais marginais de $X$ e $Y$ são expressos respectivamente na última coluna e na última linha.

Tabela 2: Representação de uma tabela de contigência.

X ⟍ Y	$B_{1}$	$B_{2}$	$\cdots$	$B_{j}$	$\cdots$	$B_{s}$	Totais em $X$
$A_{1}$	$n_{11}$	$n_{12}$	$\cdots$	$n_{1j}$	$\cdots$	$n_{1s}$	$n_{1.}$
$A_{2}$	$n_{21}$	$n_{22}$	$\cdots$	$n_{2j}$	$\cdots$	$n_{2s}$	$n_{2.}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$A_{i}$	$n_{i1}$	$n_{i2}$	$\cdots$	$n_{ij}$	$\cdots$	$n_{is}$	$n_{i.}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\cdots$	$\cdots$	$\vdots$	$\vdots$
$A_{r}$	$n_{r1}$	$n_{r2}$	$\cdots$	$n_{rj}$	$\cdots$	$n_{rs}$	$n_{r.}$
Totais em $Y$	$n_{.1}$	$n_{.2}$	$\cdots$	$n_{.j}$	$\cdots$	$n_{rs}$	$n$

Sob a hipótese de não-associação entre $X$ e $Y$ teremos que:

$\frac{n_{i1}}{n_{.1}} = \frac{n_{i2}}{n_{.2}} = \cdots = \frac{n_{is}}{n_{.s}} = \frac{n_{i.}}{n}$

e assim:

$\frac{n_{ij}}{n_{.j}} = \frac{n_{i.}}{n}$

Deste modo:

$n_{ij}^{e} = \frac{n_{i.} \times n_{.j}}{n}$

Observações

A notação $n_{ij}^{e}$ está sendo utilizada para denotar que a expressão acima determina a contagem de cada célula da tabela sob a hipótese de não associação e portanto, se refere ao valor esperado de $n_{ij}$.

Tendo definido os valores esperados em uma tabela de contingência de $r \times s$, o $\chi^2$ é dado por:

\[\chi^2 = \sum_{i=1}^{r}\sum_{j=1}^{s}\frac{(n_{ij} - n_{ij}^{e})^2}{n_{ij}^{e}}\]

Retornando ao exemplo das entrevistas

A tabela de contingência contendo os dados observados do início do capítulo pode ser escrita como:

Tabela 3: Resultados das entrevistas dos 200 munícipies.

	Não-Residente	Residente	Total Opinião
A favor	81	63	144
Contra	36	20	56
Total Moradia	117	83	200

Os Valores esperados na linha $i$ e coluna $j$ são:

Linha $1$ - Coluna $1$ (Não-Residente - A favor):

$n_{ii}^{e} = \frac{n_{1.} \times n_{.1}}{n} = \frac{144 \times 117}{200} = 84.24$

Linha $1$ - Coluna $2$ (Residente - A favor):

$n_{ii}^{e} = \frac{n_{1.} \times n_{.2}}{n} = \frac{144 \times 83}{200} = 59.76$

Linha $2$ - Coluna $1$ (Não-Residente - Contra):

$n_{ii}^{e} = \frac{n_{2.} \times n_{.1}}{n} = \frac{56 \times 117}{200} = 32.76$

Linha $2$ - Coluna $2$ (Residente - Contra):

$n_{ii}^{e} = \frac{n_{2.} \times n_{.2}}{n} = \frac{56 \times 83}{200} = 23.24$

De modo que a tabela com os valores esperados será:

Tabela 4: Valores esperados na hipótese de não-associação entre Opiniao e locals de Moradia dos 200 munícipies entrevistados.

	Não-Residente	Residente	Total Opinião
A favor	84.24	59.76	144
Contra	32.76	23.24	56
Total Moradia	117	83	200

Finalmente, o valor de $\chi^2$ pode ser calculado por:

$\chi^2 = \frac{(81 - 84.24)^2}{84.24} + \frac{(36 - 32.76)^2}{84.24} + \frac{(63 - 59.76)^2}{84.24} + \frac{(20 - 23.24)^2}{84.24} = 1.072$

6 Valores de $\chi^2$ quando existe associação

O valor de $\chi^2$ será zero somente se os valores observados forem exatamente iguais aos valores esperados. Pequenas discrepâncias irão gerar valores de $\chi^2$ acima de zero, que se tornarão mais altos à medida que aumentam as diferenças entre $n_{ij}$ e $n_{ij}^e$.

Quantificando as associações

Abaixo estão diferentes exemplos em que existe associação entre Opinião e Moradia. Compare os valores e os gráficos abaixo aos que fizemos no exemplo do capítulo e veja que todos os valores de $\chi^2$ são mais elevados.

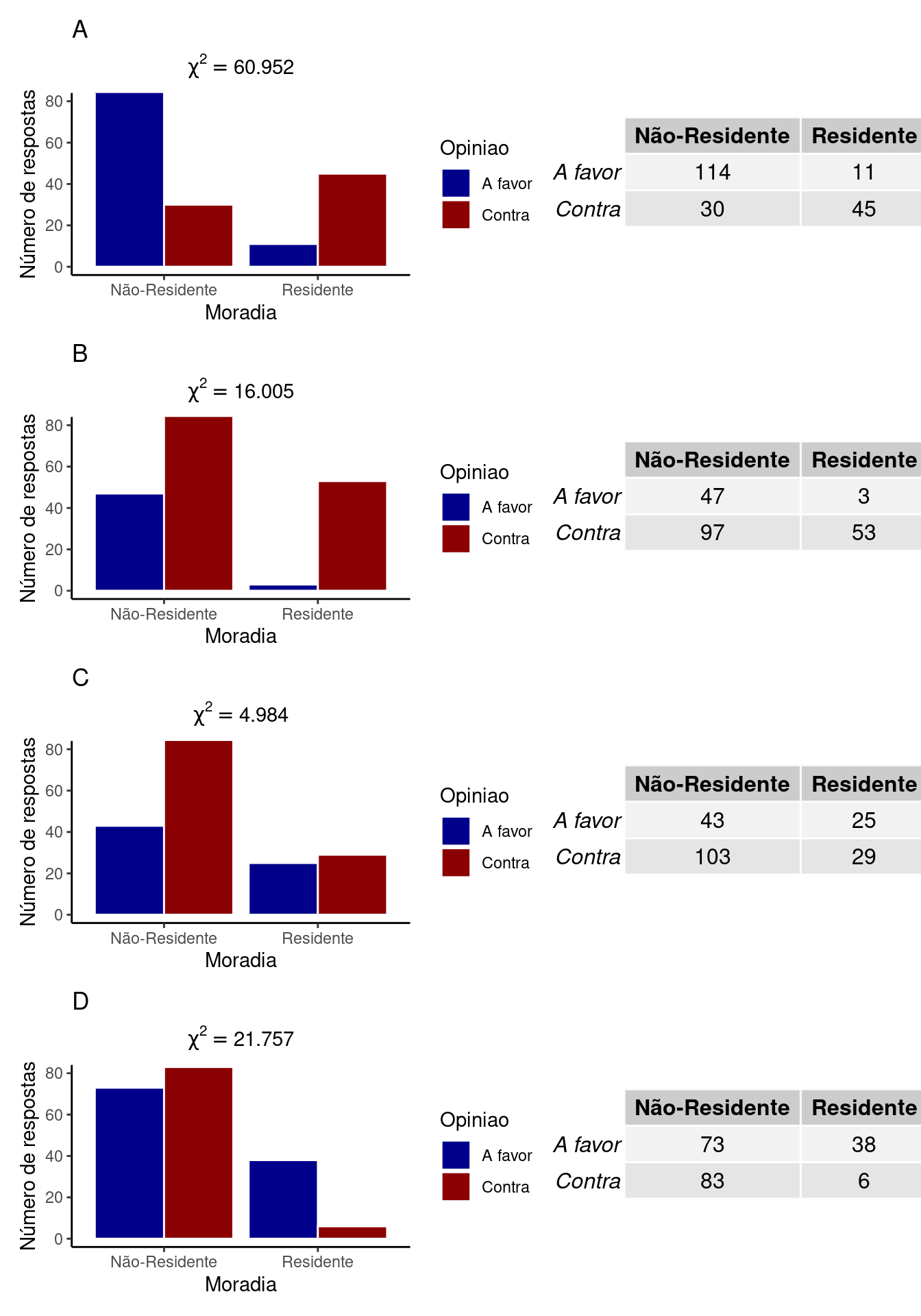
Tente aplicar a fórmula do $\chi^2$ para chegar aos resultados apresentados em cada exemplo.

7 Variações do índice de $\chi^2$

O valor de $\chi^2$ aumenta com o tamanho da amostra, o que torna difícil comparações entre diferentes estudos. Para corrigir este efeito existe o coeficiente de contigência de Pearson ($C$) que é baseado no resultado de $\chi^2$

\[C = \sqrt{\frac{\chi^2}{\chi^2 + n}}\]

em que $n$ é o tamanho da amostra.

O valor máximo de $C$ depende do número de linhas ($r$) e de colunas ($s$) na tabela de contingêcia. Podemos definir um coeficiente que esteja limitado entre $0$ e $1$:

\[T = \sqrt{\frac{\frac{\chi^2}{n}}{(r-1) \times (s-1)}}\] O valor $T = 0$ ocorre quando não há associação ($\chi^2 = 0$) e o valor máximo de $T = 1$ só será atingido se houver associação e $r = s$

8 Obtendo o índice de $\chi^2$ de uma tabela de dados

A função para o cálculo do $\chi^2$ no R é chisq.test e pode ser utilizada a partir da tabela de contigência gerada pela função table:

tcont = table(mun$Opiniao, mun$Moradia)
chisq.test(tcont)


    Pearson's Chi-squared test with Yates' continuity correction

data:  tcont
X-squared = 0.76697, df = 1, p-value = 0.3812

O resultado mostra o o valor de $\chi^2$ calculado (X-squared) e outras duas quantias denominadas de graus de liberdade (df) e valor de p (p-value), tópicos abordados em inferência estatística.

Note que o resultado é diferente do que obtivemos neste capítulo. Isto ocorre pois, por padrão, a função utiliza a correção de Yates, em que $\chi_{Yates}^{2}$ é calculado por:

\[\chi_{Yates}^{2} = \sum_{i=1}^{r}\sum_{j=1}^{s}\frac{(|n_{ij} - n_{ij}^{e}| - 0,5)^2}{n_{ij}^{e}}\]

O termo $|n_{ij} - n_{ij}^{e}|$ se refere ao módulo da distância entre os valores observados e calculados.

Se quisermos obter exatamente os resultados descritos no exemplo deste capítulo, basta fazermos:

chisq.test(tcont, correct = FALSE)


    Pearson's Chi-squared test

data:  tcont
X-squared = 1.0724, df = 1, p-value = 0.3004

X ⟍ Y	\(B_{1}\)	\(B_{2}\)	\(\cdots\)	\(B_{j}\)	\(\cdots\)	\(B_{s}\)	Totais em \(X\)
\(A_{1}\)	\(n_{11}\)	\(n_{12}\)	\(\cdots\)	\(n_{1j}\)	\(\cdots\)	\(n_{1s}\)	\(n_{1.}\)
\(A_{2}\)	\(n_{21}\)	\(n_{22}\)	\(\cdots\)	\(n_{2j}\)	\(\cdots\)	\(n_{2s}\)	\(n_{2.}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(A_{i}\)	\(n_{i1}\)	\(n_{i2}\)	\(\cdots\)	\(n_{ij}\)	\(\cdots\)	\(n_{is}\)	\(n_{i.}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\cdots\)	\(\cdots\)	\(\vdots\)	\(\vdots\)
\(A_{r}\)	\(n_{r1}\)	\(n_{r2}\)	\(\cdots\)	\(n_{rj}\)	\(\cdots\)	\(n_{rs}\)	\(n_{r.}\)
Totais em \(Y\)	\(n_{.1}\)	\(n_{.2}\)	\(\cdots\)	\(n_{.j}\)	\(\cdots\)	\(n_{rs}\)	\(n\)

Associação entre duas variáveis qualitativas

1 Tabelas de frequência e gráficos de barras

2 Tabelas de contingência

3 O gráfico de barras para duas variáveis qualitativas

4 Medindo a discrepância com o índice de \(\chi^2\) de Pearson

5 O índice de \(\chi^2\) em uma tabela de contigência

6 Valores de \(\chi^2\) quando existe associação

7 Variações do índice de \(\chi^2\)

8 Obtendo o índice de \(\chi^2\) de uma tabela de dados