Medidas de Associação e Relacionamentos entre Variáveis com Python

Análise de associações entre variáveis usando Python com Pandas, Matplotlib e Seaborn, incluindo tabelas de contingência, correlação e visualizações.

Neste tutorial, exploraremos como analisar padrões de associação entre diferentes tipos de variáveis em Python, utilizando o dataset de pinguins de Palmer.

Código em Python

Acompanha este tutorial o Medidas de associação em Python

1 Pacotes necessários

import pandas as pd
import matplotlib.pyplot as plt
from palmerpenguins import load_penguins
import seaborn as sns
import numpy as np

2 Carregando e preparando os dados

penguins = load_penguins().dropna()
penguins.shape

(333, 8)

# Visualizando as primeiras linhas
penguins.head()

	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex	year
0	Adelie	Torgersen	39.1	18.7	181.0	3750.0	male	2007
1	Adelie	Torgersen	39.5	17.4	186.0	3800.0	female	2007
2	Adelie	Torgersen	40.3	18.0	195.0	3250.0	female	2007
4	Adelie	Torgersen	36.7	19.3	193.0	3450.0	female	2007
5	Adelie	Torgersen	39.3	20.6	190.0	3650.0	male	2007

3 Associação entre Duas Variáveis Qualitativas (Categóricas)

Quando queremos analisar a relação entre duas variáveis categóricas, utilizamos tabelas de contingência.

3.1 Exemplo: Associação entre Espécie e Ilha

# Tabela de contingência (frequências observadas)
contingency_table = pd.crosstab(penguins['species'], 
                                penguins['island'])
contingency_table

island	Biscoe	Dream	Torgersen
species
Adelie	44	55	47
Chinstrap	0	68	0
Gentoo	119	0	0

3.2 Frequências Relativas

# Frequências relativas por linha (marginais)
total_row = contingency_table.sum(axis=1)
relative_row = contingency_table.div(total_row, axis=0)
print("Frequências relativas por linha (espécie):")
relative_row

Frequências relativas por linha (espécie):

island	Biscoe	Dream	Torgersen
species
Adelie	0.30137	0.376712	0.321918
Chinstrap	0.00000	1.000000	0.000000
Gentoo	1.00000	0.000000	0.000000

# Frequências relativas por coluna (marginais)
total_col = contingency_table.sum(axis=0)
relative_col = contingency_table.div(total_col, axis=1)
print("Frequências relativas por coluna (ilha):")
relative_col

Frequências relativas por coluna (ilha):

island	Biscoe	Dream	Torgersen
species
Adelie	0.269939	0.447154	1.0
Chinstrap	0.000000	0.552846	0.0
Gentoo	0.730061	0.000000	0.0

# Frequências relativas conjuntas
relative_joint = contingency_table / contingency_table.sum().sum()
print("Frequências relativas conjuntas:")
relative_joint

Frequências relativas conjuntas:

island	Biscoe	Dream	Torgersen
species
Adelie	0.132132	0.165165	0.141141
Chinstrap	0.000000	0.204204	0.000000
Gentoo	0.357357	0.000000	0.000000

3.3 Visualização: Gráfico de Barras Agrupadas

contingency_table.plot(kind='bar', stacked=False, figsize=(8, 6))
plt.title("Associação entre Espécie e Ilha")
plt.xlabel("Espécie")
plt.ylabel("Frequência")
plt.legend(title="Ilha")
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()
plt.close('all')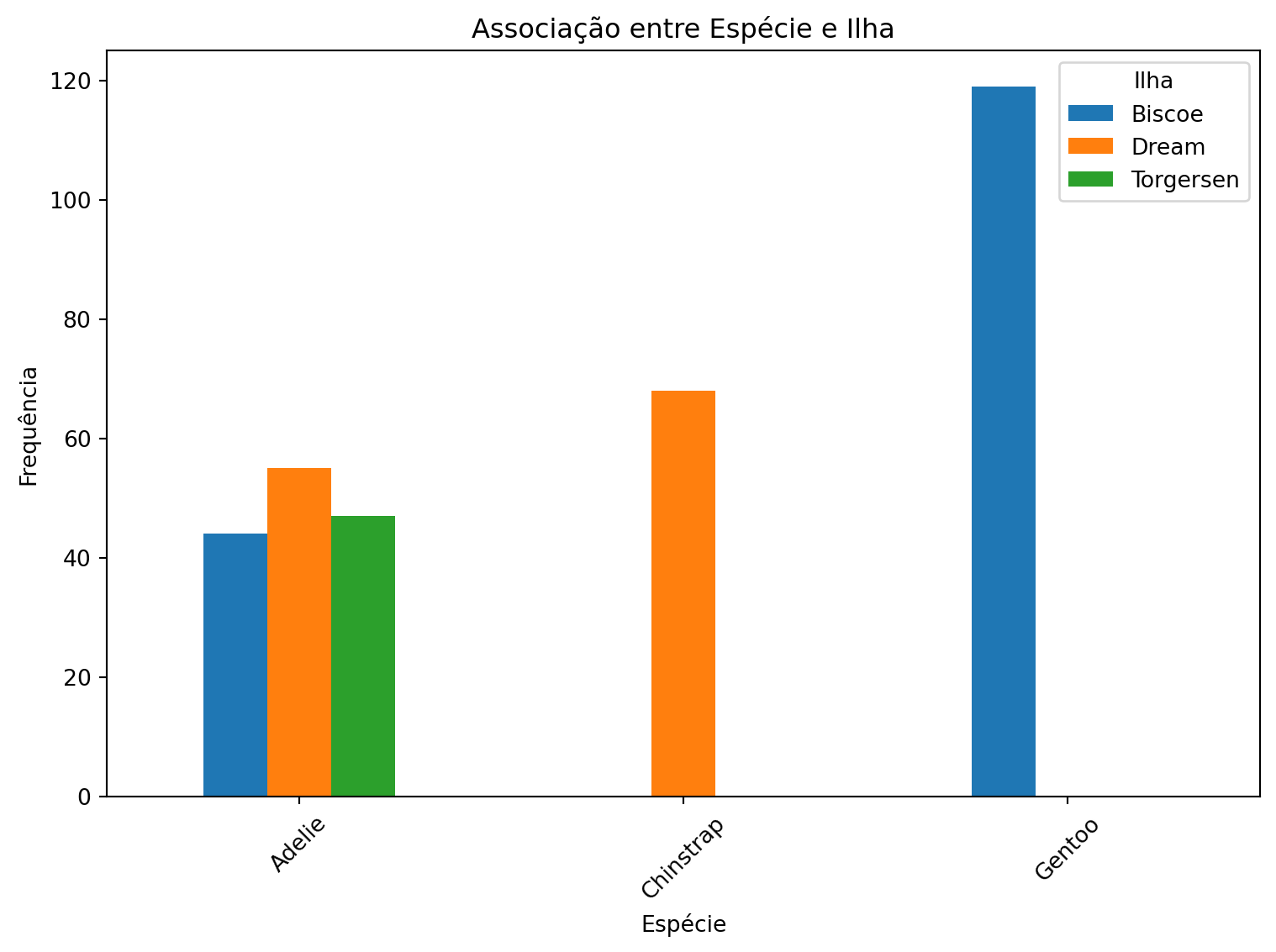

# Gráfico alternativo com Seaborn
plt.figure(figsize=(8, 6))
sns.countplot(data=penguins, x='species', hue='island')
plt.title("Distribuição de Espécies por Ilha")
plt.xlabel("Espécie")
plt.ylabel("Frequência")
plt.legend(title="Ilha")
plt.show()
plt.close('all')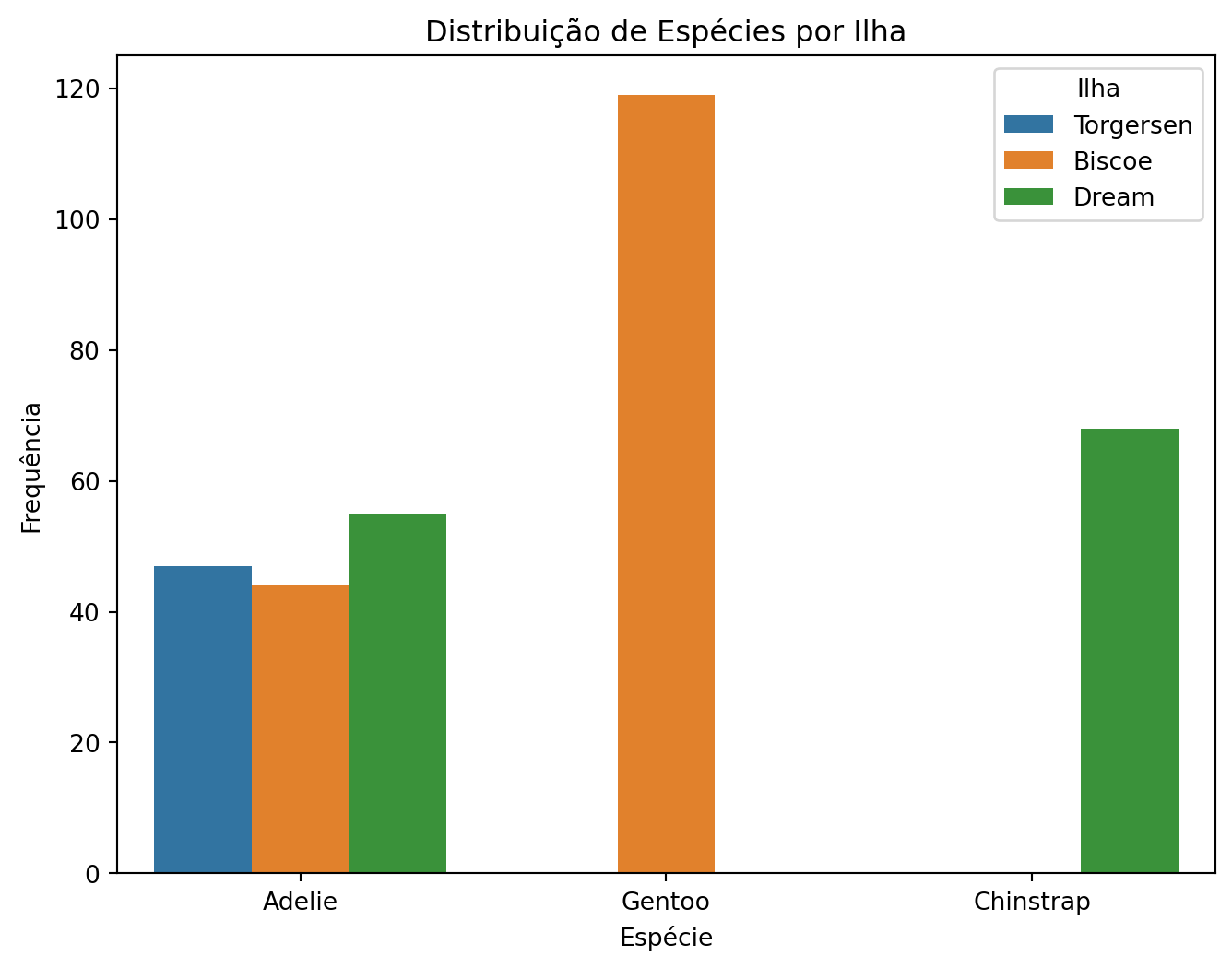

Nota

Interpretando a associação:
- Se as proporções fossem similares em todas as categorias, não haveria associação
- Diferenças significativas nas proporções indicam possível associação
- No exemplo, vemos que diferentes espécies têm distribuições distintas entre as ilhas

4 Associação entre Duas Variáveis Quantitativas

Para variáveis quantitativas, utilizamos correlação e covariância.

4.1 Exemplo: Comprimento do Bico vs Massa Corporal

# Gráfico de dispersão
plt.figure(figsize=(10, 6))
sns.scatterplot(
    data=penguins,
    x='bill_length_mm',
    y='body_mass_g',
    hue='species',
    s=60
)
plt.title("Associação entre Comprimento do Bico e Massa Corporal")
plt.xlabel("Comprimento do Bico (mm)")
plt.ylabel("Massa Corporal (g)")
plt.show()
plt.close('all')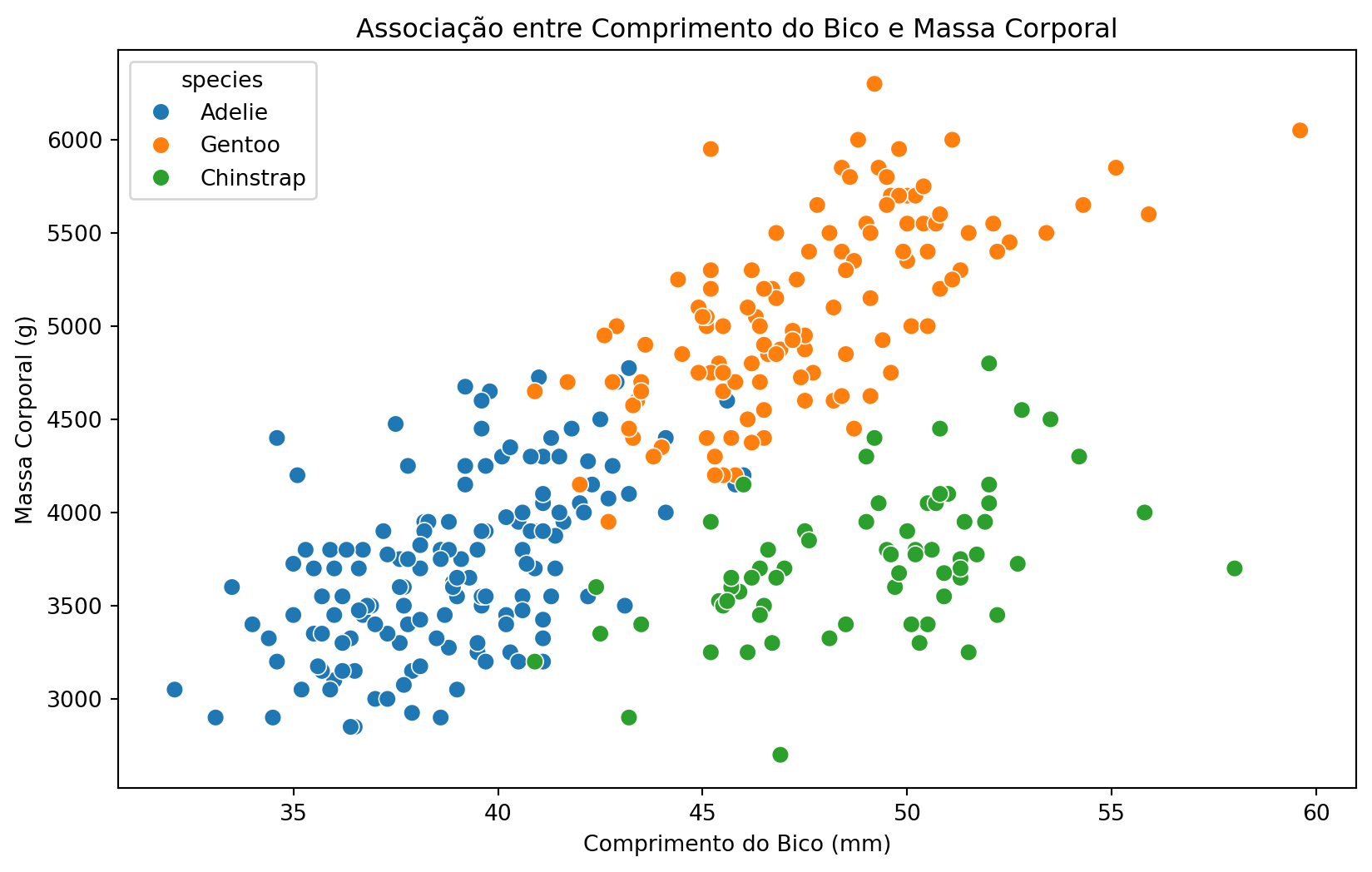

4.2 Covariância e Correlação

# Covariância
covariance = penguins[['bill_length_mm', 'body_mass_g']].cov()
print("Matriz de Covariância:")
covariance

Matriz de Covariância:

	bill_length_mm	body_mass_g
bill_length_mm	29.906333	2595.623304
body_mass_g	2595.623304	648372.487699

# Correlação de Pearson
correlation = penguins[['bill_length_mm', 'body_mass_g']].corr()
print("Matriz de Correlação:")
correlation

Matriz de Correlação:

	bill_length_mm	body_mass_g
bill_length_mm	1.000000	0.589451
body_mass_g	0.589451	1.000000

4.3 Entendendo a Correlação como Covariância Padronizada

# Padronizando as variáveis (Z-score)
penguins_padr = penguins[['bill_length_mm', 'body_mass_g']].copy()
penguins_padr = (penguins_padr - penguins_padr.mean()) / penguins_padr.std()

print("Média das variáveis padronizadas:", penguins_padr.mean().values)
print("Desvio padrão das variáveis padronizadas:", penguins_padr.std().values)

Média das variáveis padronizadas: [-9.38855266e-16 -8.53504788e-17]
Desvio padrão das variáveis padronizadas: [1. 1.]

# A covariância de variáveis padronizadas = correlação
print("Covariância das variáveis padronizadas:")
penguins_padr.cov()

Covariância das variáveis padronizadas:

	bill_length_mm	body_mass_g
bill_length_mm	1.000000	0.589451
body_mass_g	0.589451	1.000000

5 3. Associação entre Variável Quantitativa e Qualitativa

5.1 Exemplo: Massa Corporal por Espécie

# Resumo descritivo por grupo
grouped_mass = penguins.groupby('species')['body_mass_g'].describe()
grouped_mass

	count	mean	std	min	25%	50%	75%	max
species
Adelie	146.0	3706.164384	458.620135	2850.0	3362.5	3700.0	4000.0	4775.0
Chinstrap	68.0	3733.088235	384.335081	2700.0	3487.5	3700.0	3950.0	4800.0
Gentoo	119.0	5092.436975	501.476154	3950.0	4700.0	5050.0	5500.0	6300.0

# Para outra variável
grouped_bill = penguins.groupby('species')['bill_length_mm'].describe()
grouped_bill

	count	mean	std	min	25%	50%	75%	max
species
Adelie	146.0	38.823973	2.662597	32.1	36.725	38.85	40.775	46.0
Chinstrap	68.0	48.833824	3.339256	40.9	46.350	49.55	51.075	58.0
Gentoo	119.0	47.568067	3.106116	40.9	45.350	47.40	49.600	59.6

5.2 Visualização: Boxplot por Grupos

plt.figure(figsize=(10, 6))
sns.boxplot(x='species', y='body_mass_g', data=penguins)
plt.title("Distribuição da Massa Corporal por Espécie")
plt.xlabel("Espécie")
plt.ylabel("Massa Corporal (g)")
plt.show()
plt.close('all')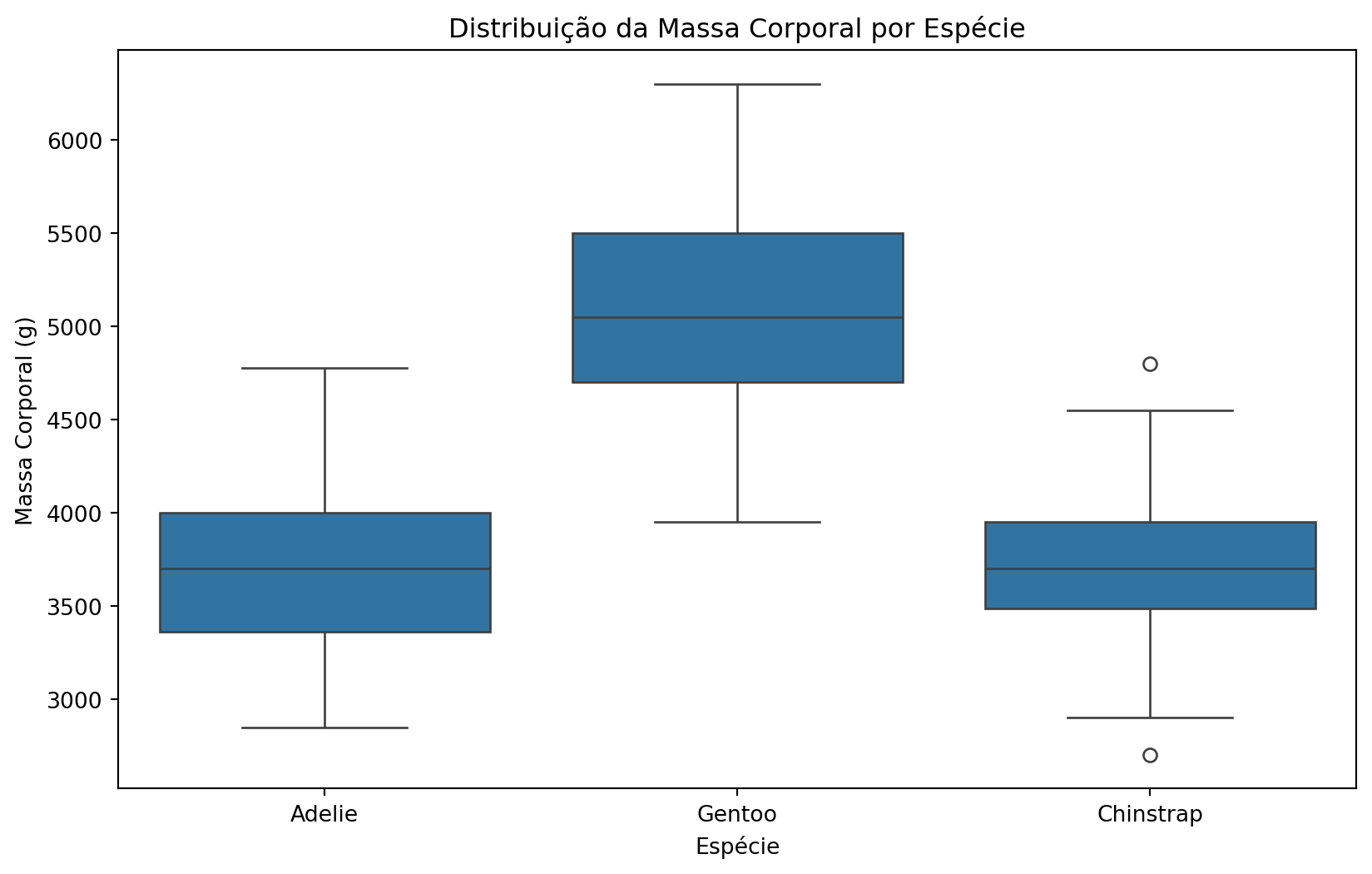

5.3 Gráfico de Médias com Barras de Erro

plt.figure(figsize=(10, 6))
sns.pointplot(
    data=penguins,
    x='species',
    y='body_mass_g',
    capsize=0.1,
    color='black',
    errorbar='sd'
)
plt.title("Média e Desvio Padrão da Massa Corporal por Espécie")
plt.xlabel("Espécie")
plt.ylabel("Massa Corporal (g)")
plt.show()
plt.close('all')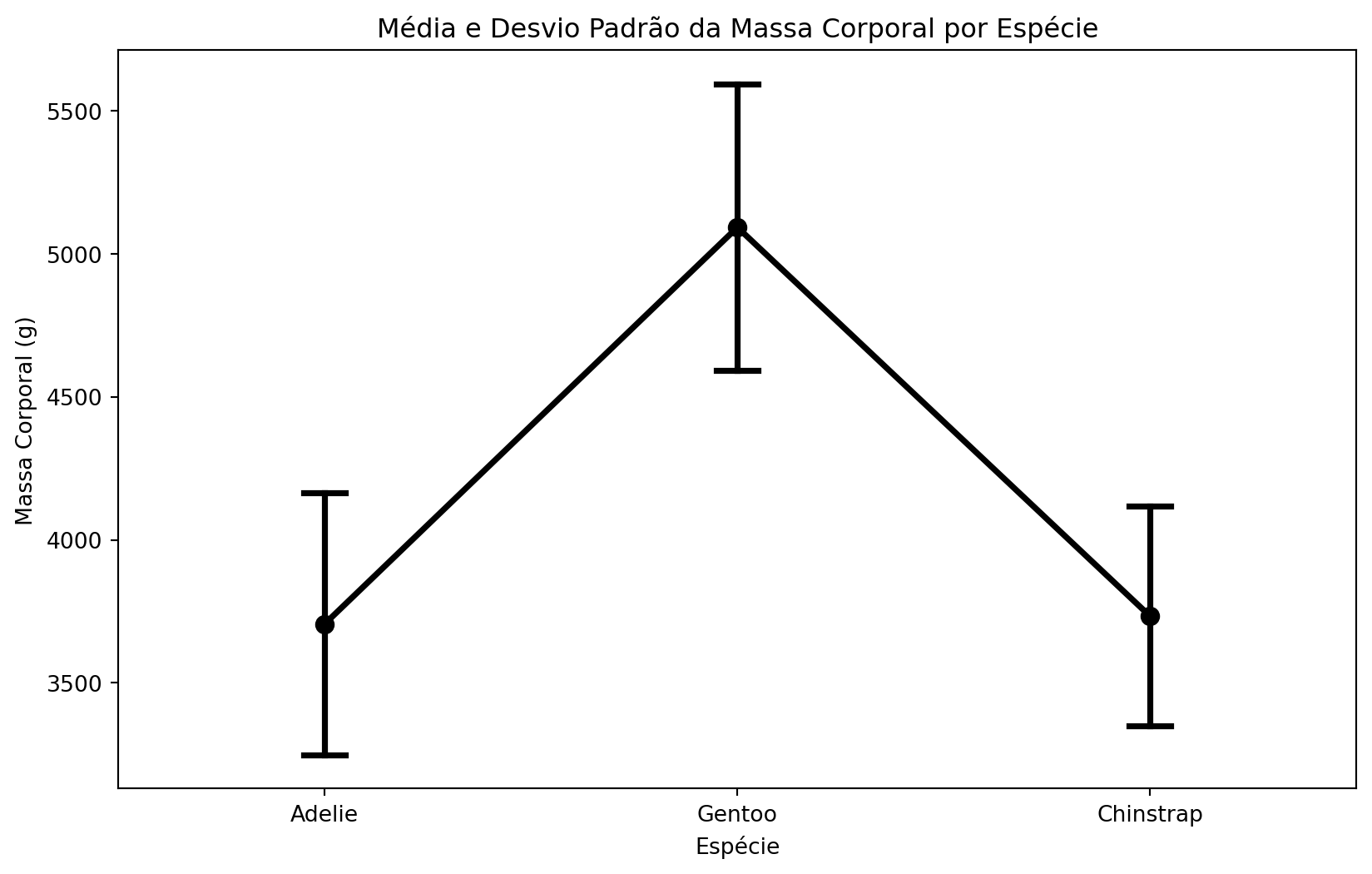

Nota

Interpretando boxplots por grupos:
- Medianas diferentes: Indica diferenças entre os grupos
- Sobreposição das caixas: Grupos com distribuições similares
- Outliers: Valores atípicos em cada grupo

6 Análises Multivariadas

6.1 Scatter Plot com Múltiplas Dimensões

plt.figure(figsize=(10, 6))
sns.scatterplot(
    data=penguins,
    x='bill_length_mm',
    y='body_mass_g',
    hue='species',
    size='flipper_length_mm',
    sizes=(50, 200)
)
plt.title("Massa Corporal vs Comprimento do Bico (tamanho = comprimento da nadadeira)")
plt.xlabel("Comprimento do Bico (mm)")
plt.ylabel("Massa Corporal (g)")
plt.show()
plt.close('all')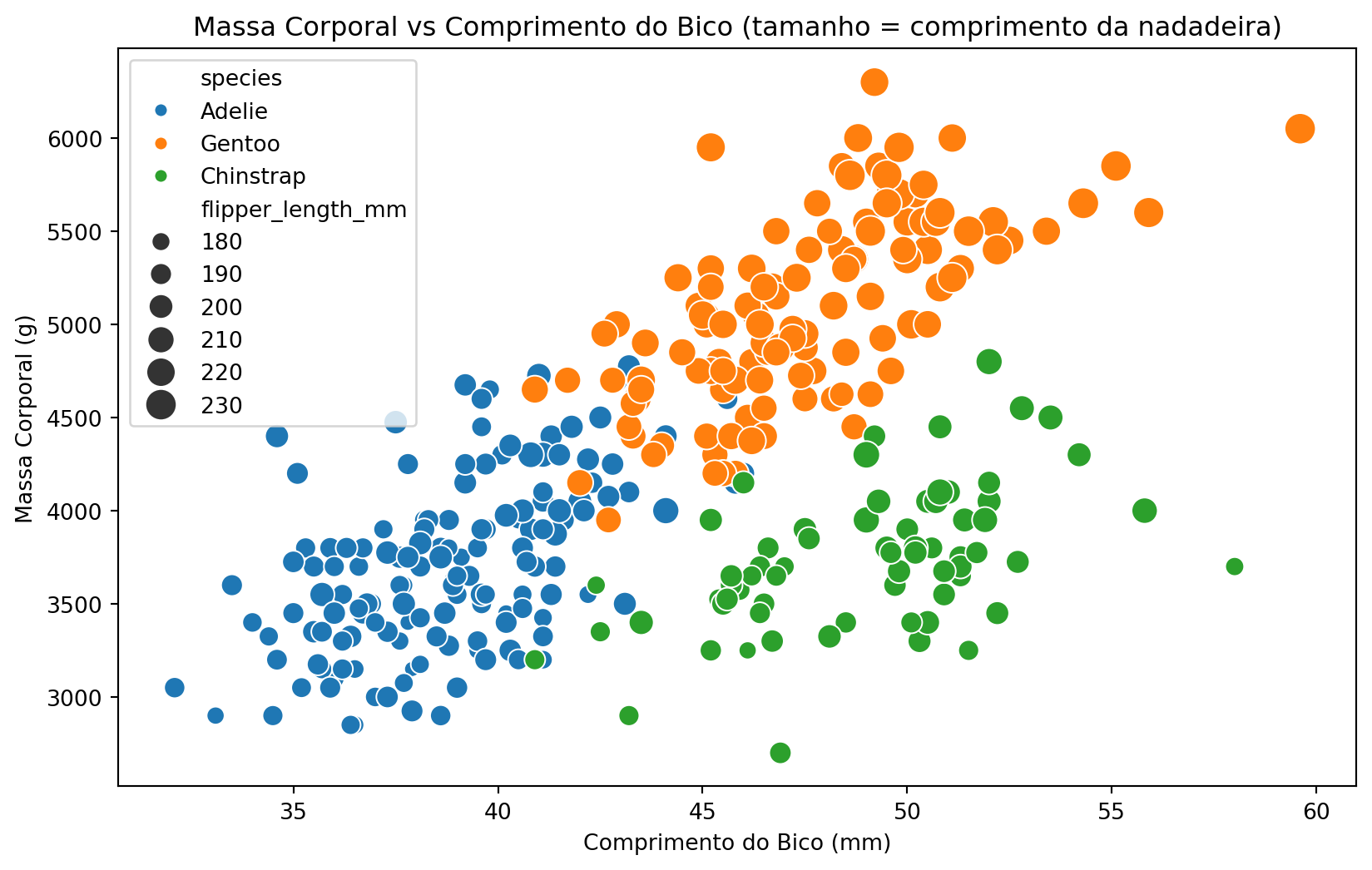

6.2 Regressão Linear por Grupos

sns.lmplot(
    data=penguins,
    x='bill_length_mm',
    y='body_mass_g',
    hue='species',
    height=6,
    aspect=1.2,
    markers=['o', 's', 'D'],
    ci=None
)
plt.title("Regressão Linear: Massa Corporal vs Comprimento do Bico por Espécie")
plt.show()
plt.close('all')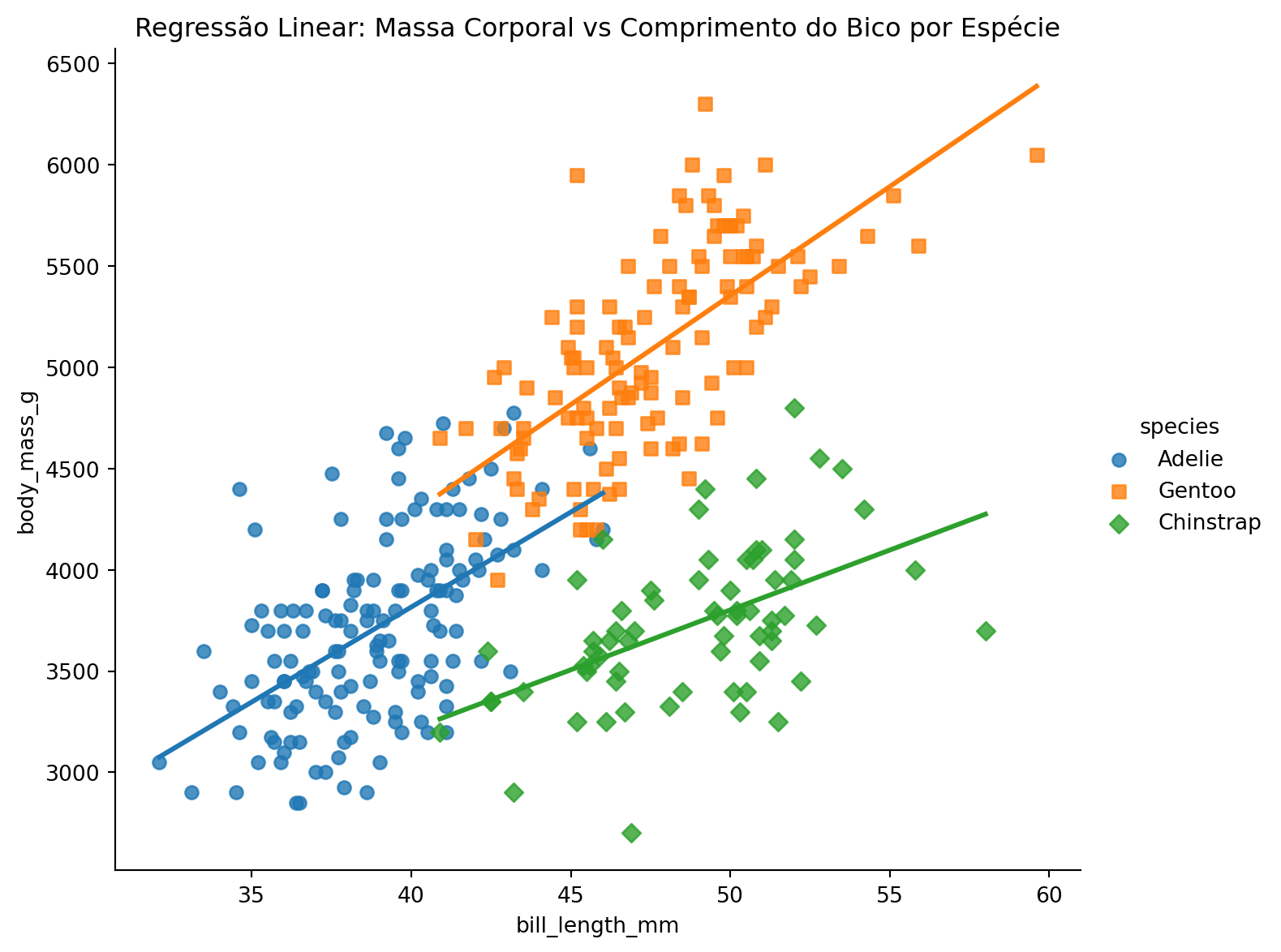

6.3 Pairplot: Todas as Combinações de Variáveis

# Matriz de gráficos de dispersão
sns.pairplot(
    data=penguins,
    vars=['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g'],
    hue='species',
    diag_kind='kde',
    height=2.5
)
plt.show()
plt.close('all')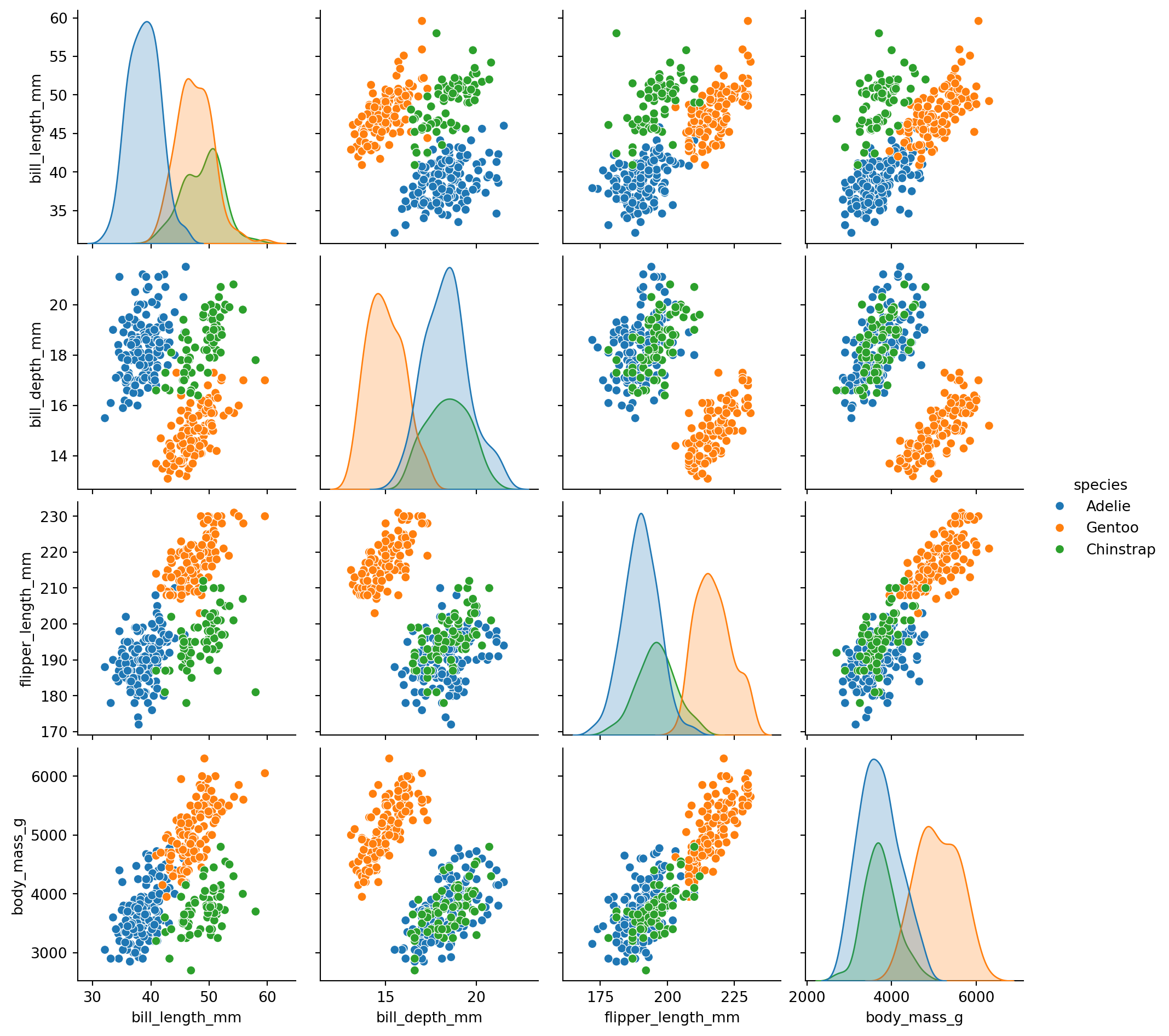

6.4 Matriz de Correlação Completa

# Calcular correlações para todas as variáveis numéricas
numeric_vars = ['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']
correlation_matrix = penguins[numeric_vars].corr()

# Heatmap da matriz de correlação
plt.figure(figsize=(8, 6))
sns.heatmap(
    correlation_matrix,
    annot=True,
    cmap='coolwarm',
    center=0,
    square=True,
    fmt='.2f'
)
plt.title("Matriz de Correlação das Variáveis Quantitativas")
plt.tight_layout()
plt.show()
plt.close('all')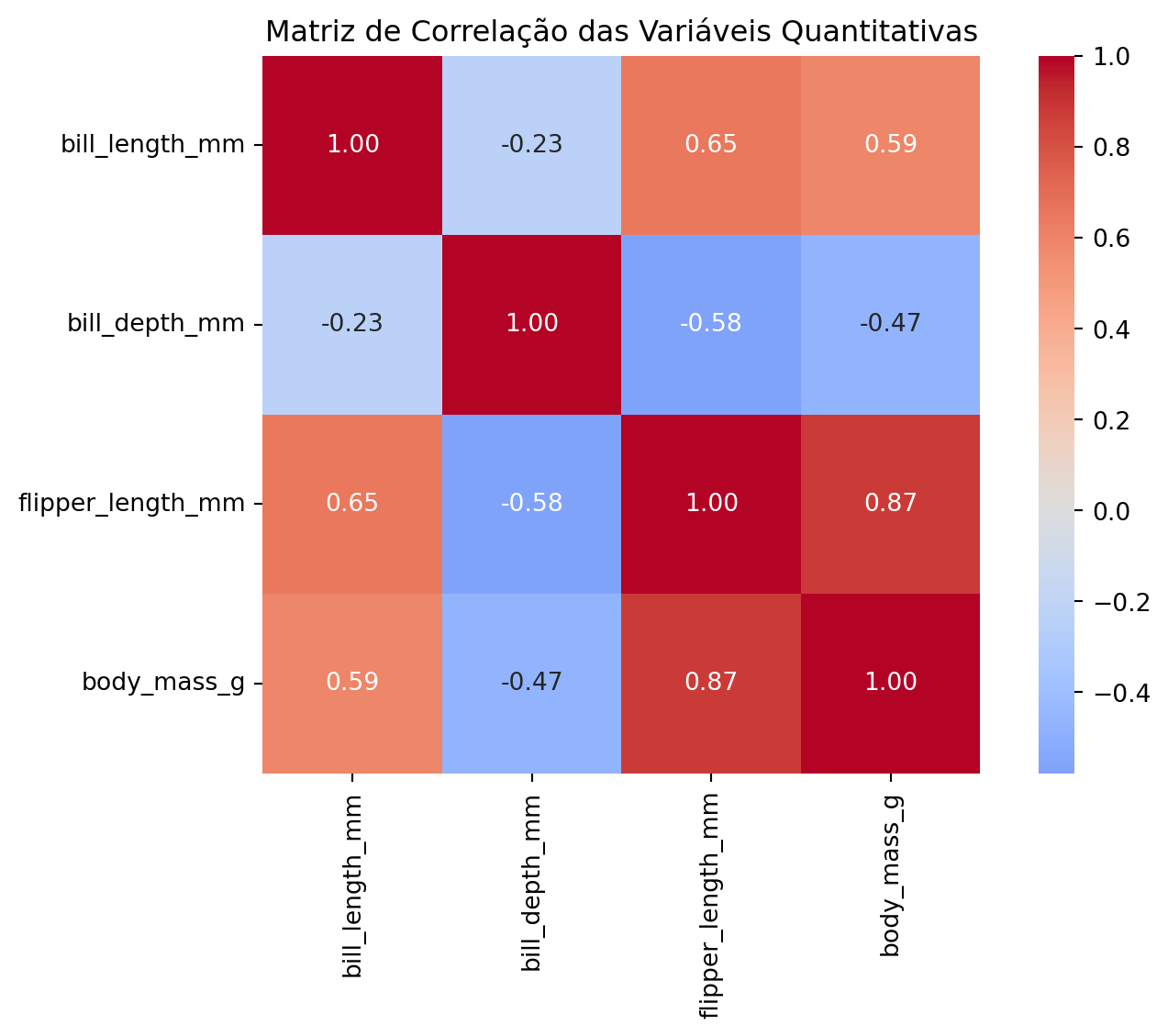

7 Exemplos Adicionais de Visualização

7.1 Comprimento da Nadadeira vs Massa Corporal

sns.lmplot(
    data=penguins,
    x='flipper_length_mm',
    y='body_mass_g',
    hue='species',
    height=6,
    aspect=1.2,
    markers=['o', 's', 'D'],
    ci=None
)
plt.title("Massa Corporal vs Comprimento da Nadadeira por Espécie")
plt.show()
plt.close('all')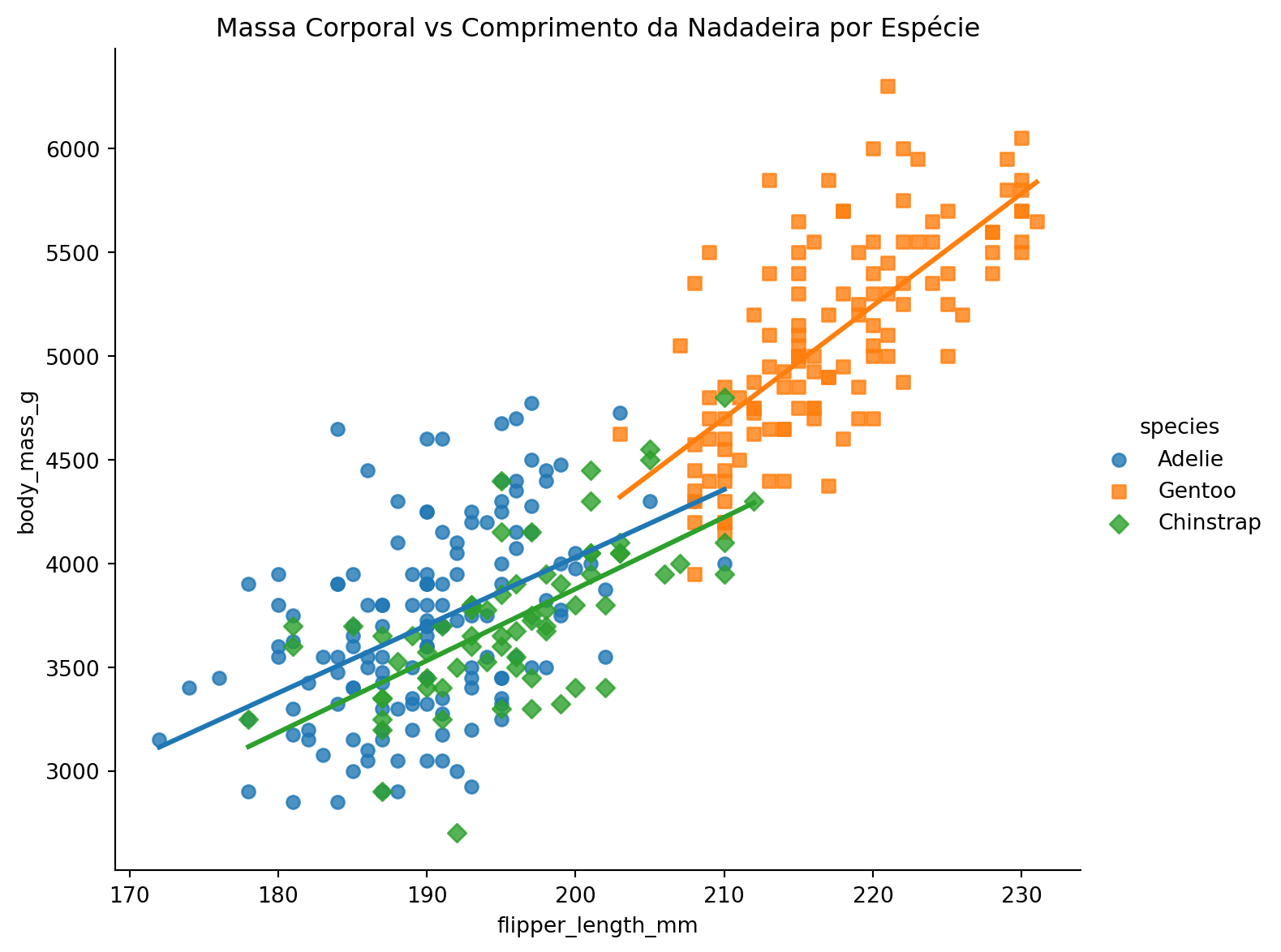

7.2 Altura vs Comprimento do Bico

sns.lmplot(
    data=penguins,
    x='bill_depth_mm',
    y='bill_length_mm',
    hue='species',
    height=6,
    aspect=1.2,
    markers=['o', 's', 'D'],
    ci=None
)
plt.title("Comprimento vs Altura do Bico por Espécie")
plt.show()
plt.close('all')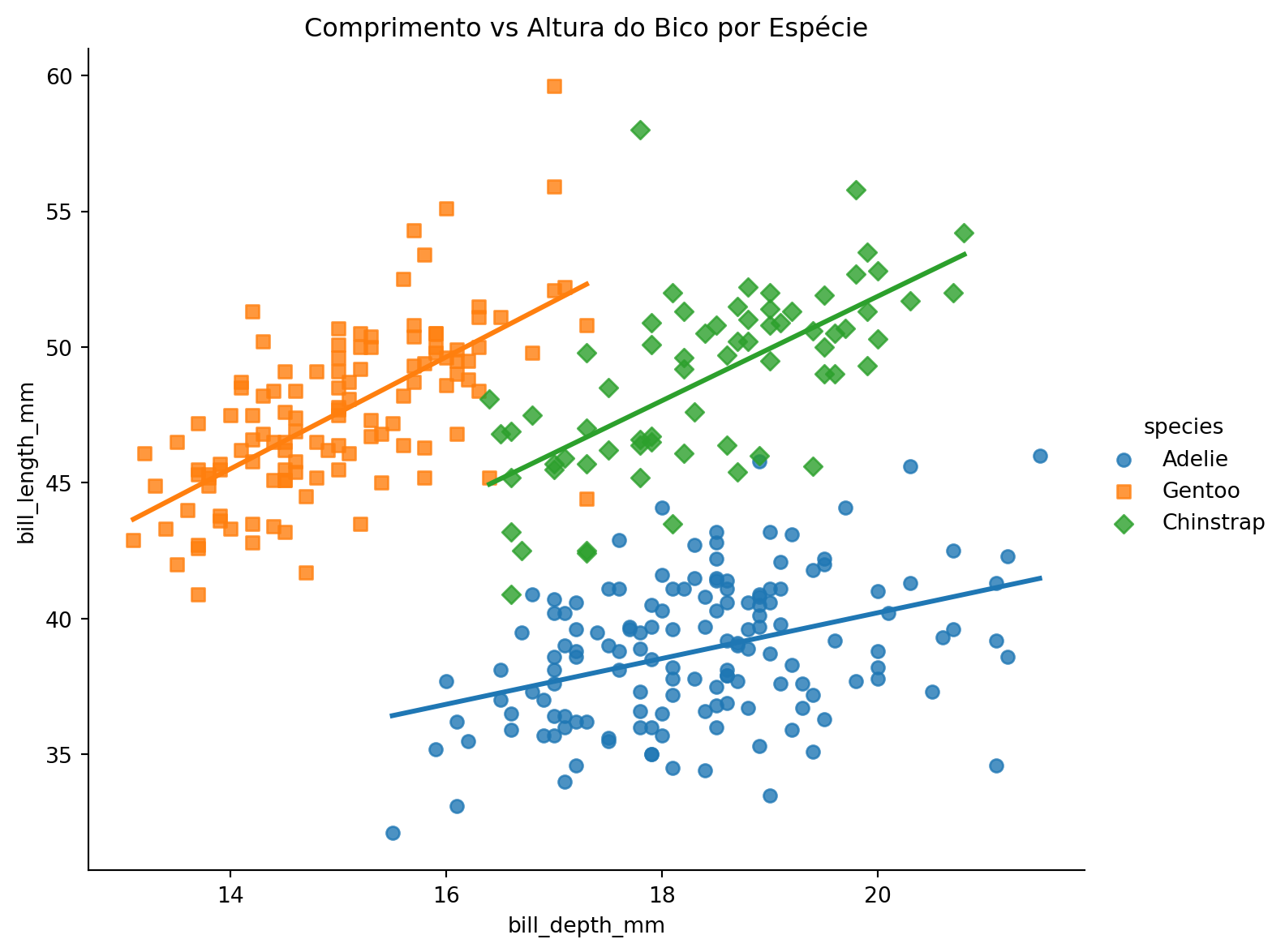

8 Resumo dos Tipos de Associação

Tipos de Variáveis	Medidas	Visualizações
Qualitativa vs Qualitativa	Tabelas de contingência, frequências relativas	Barras agrupadas, countplot
Quantitativa vs Quantitativa	Correlação, covariância	Scatter plot, pairplot
Quantitativa vs Qualitativa	Estatísticas por grupo (média, mediana)	Boxplot, pointplot
Multivariada	Correlações múltiplas	Pairplot, heatmap, lmplot

9 Dicas Práticas

9.1 Escolhendo a visualização adequada

# Para escolher o gráfico certo, considere:
print("Tipos de dados:")
print(penguins.dtypes)

Tipos de dados:
species               object
island                object
bill_length_mm       float64
bill_depth_mm        float64
flipper_length_mm    float64
body_mass_g          float64
sex                   object
year                   int64
dtype: object

9.2 Identificando correlações interessantes

# Encontrar as maiores correlações
corr_matrix = penguins[numeric_vars].corr()
# Remover a diagonal (correlação de uma variável consigo mesma)
corr_matrix_clean = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(bool))

# Empilhar e ordenar por valor absoluto
correlations = corr_matrix_clean.stack().sort_values(key=abs, ascending=False)
print("Correlações mais fortes:")
correlations.head()

Correlações mais fortes:

flipper_length_mm  body_mass_g          0.872979
bill_length_mm     flipper_length_mm    0.653096
                   body_mass_g          0.589451
bill_depth_mm      flipper_length_mm   -0.577792
                   body_mass_g         -0.472016
dtype: float64