Estatística Descritiva e Visualização com Python

Análise descritiva de dados usando Python com Pandas e Matplotlib, incluindo medidas de tendência central, dispersão e visualizações básicas.

Neste tutorial, exploraremos como realizar análise estatística descritiva em Python, utilizando o dataset de [pinguins de Palmer](https://allisonhorst.github.io/palmerpenguins/index.html}{target=“_blank”} para exemplificar conceitos fundamentais de estatística.

Código em Python

Acompanha este tutorial o Estatística descritiva em Python

1 Pacotes necessários

import pandas as pd
import numpy as np
from palmerpenguins import load_penguins
import matplotlib.pyplot as plt

2 Carregando e preparando os dados

penguins = load_penguins().dropna()  # Remove valores ausentes
penguins.shape  # Verificar dimensões

(333, 8)

3 Variáveis Qualitativas (Categóricas)

3.1 Identificando tipos de dados

penguins.dtypes

species               object
island                object
bill_length_mm       float64
bill_depth_mm        float64
flipper_length_mm    float64
body_mass_g          float64
sex                   object
year                   int64
dtype: object

3.2 Frequência absoluta

penguins['species'].value_counts()

species
Adelie       146
Gentoo       119
Chinstrap     68
Name: count, dtype: int64

3.3 Frequência relativa

penguins['species'].value_counts(normalize=True)

species
Adelie       0.438438
Gentoo       0.357357
Chinstrap    0.204204
Name: proportion, dtype: float64

3.4 Visualização: Gráfico de barras

penguins['species'].value_counts().plot(kind='bar')
plt.title("Número de Pinguins por Espécie")
plt.xlabel("Espécie")
plt.ylabel("Frequência")
plt.show()
plt.close('all')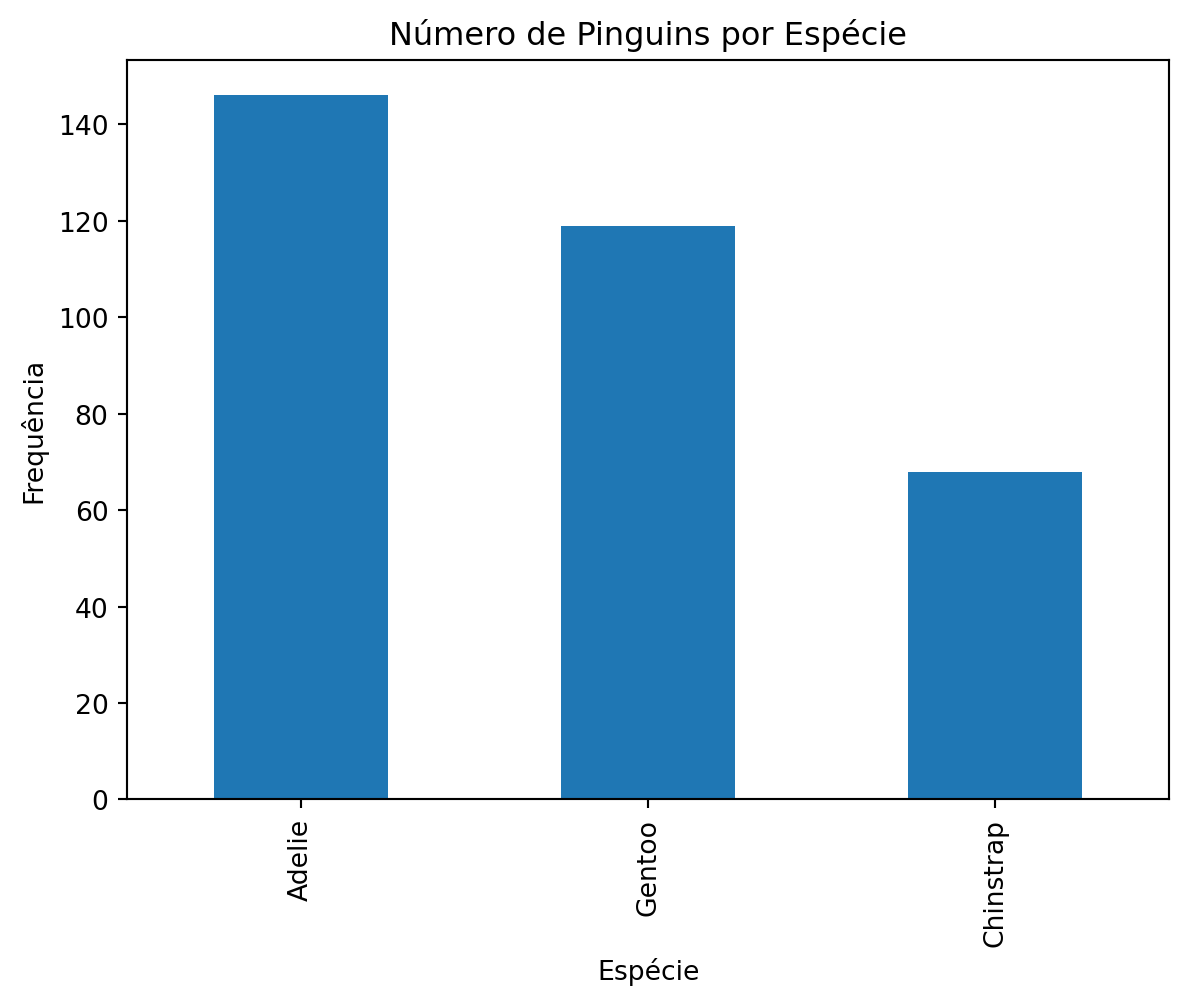

# Para outra variável categórica
penguins['island'].value_counts().plot(kind='bar')
plt.title("Distribuição de Pinguins por Ilha")
plt.xlabel("Ilha")
plt.ylabel("Frequência")
plt.show()
plt.close('all')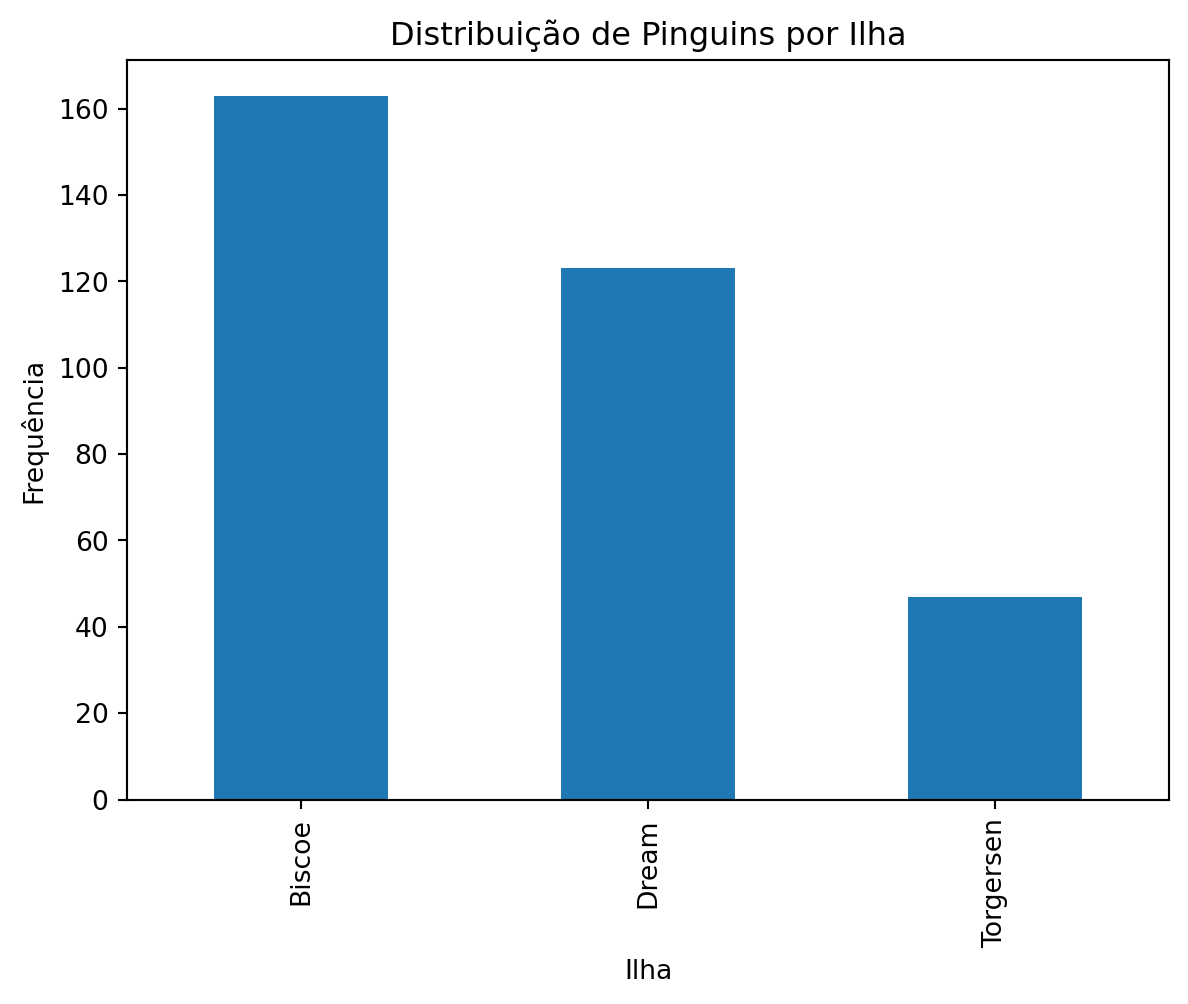

4 Variáveis Quantitativas

4.1 Resumo descritivo básico

penguins['body_mass_g'].describe()

count     333.000000
mean     4207.057057
std       805.215802
min      2700.000000
25%      3550.000000
50%      4050.000000
75%      4775.000000
max      6300.000000
Name: body_mass_g, dtype: float64

# Para todas as variáveis numéricas
penguins.describe()

	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	year
count	333.000000	333.000000	333.000000	333.000000	333.000000
mean	43.992793	17.164865	200.966967	4207.057057	2008.042042
std	5.468668	1.969235	14.015765	805.215802	0.812944
min	32.100000	13.100000	172.000000	2700.000000	2007.000000
25%	39.500000	15.600000	190.000000	3550.000000	2007.000000
50%	44.500000	17.300000	197.000000	4050.000000	2008.000000
75%	48.600000	18.700000	213.000000	4775.000000	2009.000000
max	59.600000	21.500000	231.000000	6300.000000	2009.000000

4.2 Visualização: Histograma

penguins['body_mass_g'].plot(kind='hist', 
                            bins=5, 
                            edgecolor="white")
plt.title("Histograma da Massa Corporal")
plt.xlabel("Massa (g)")
plt.ylabel("Frequência")
plt.show()
plt.close('all')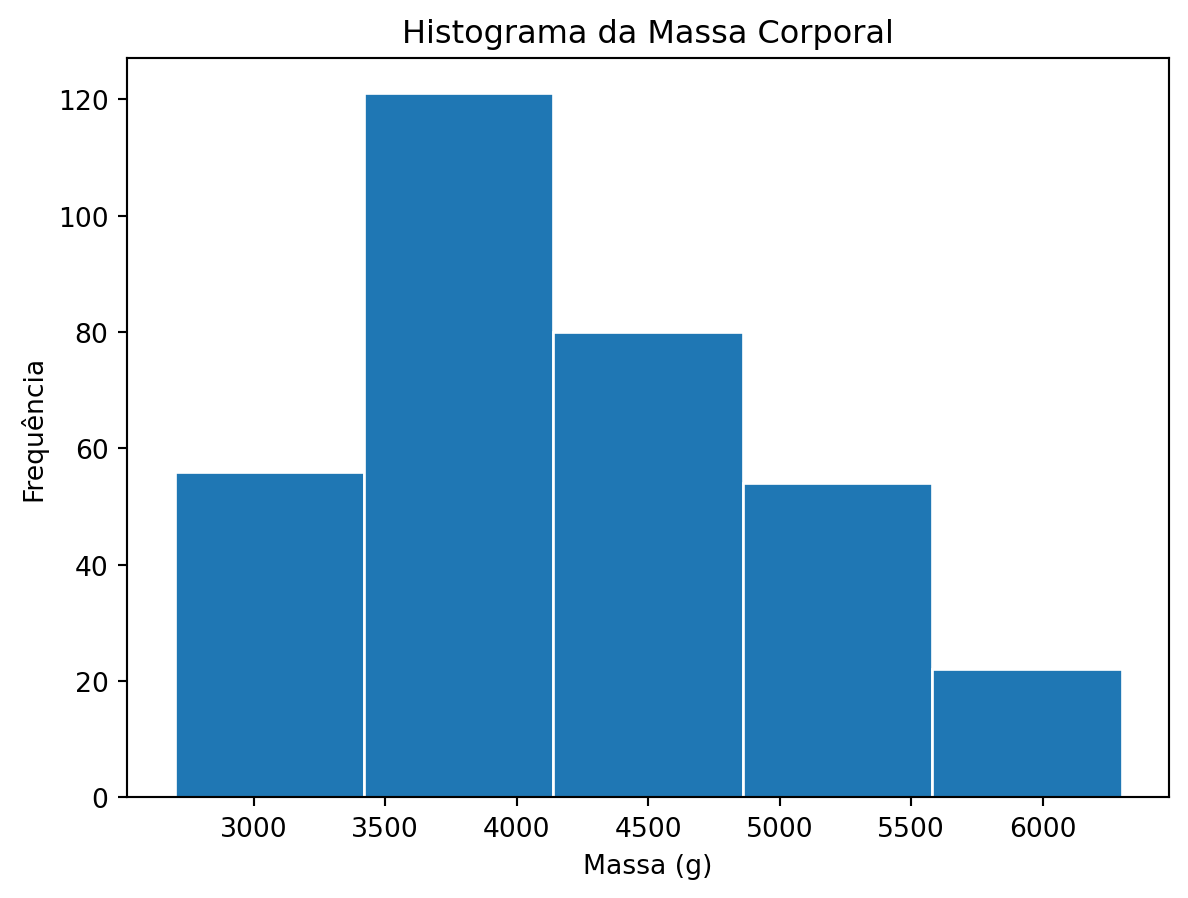

Dica

Interpretando histogramas:
- Forma: simétrica, assimétrica à esquerda/direita
- Tendência central: onde se concentram os dados
- Dispersão: quão espalhados estão os valores

5 Quartis e Medidas de Posição

5.1 Quartis individuais

penguins['body_mass_g'].quantile(0.25)  # Q1
penguins['body_mass_g'].quantile(0.50)  # Q2 (mediana)
penguins['body_mass_g'].quantile(0.75)  # Q3

np.float64(4775.0)

5.2 Múltiplos quantis

penguins['body_mass_g'].quantile([0.25, 0.5, 0.75])

0.25    3550.0
0.50    4050.0
0.75    4775.0
Name: body_mass_g, dtype: float64

5.3 Visualização: Boxplot

penguins['body_mass_g'].plot(kind='box')
plt.title("Boxplot da Massa Corporal")
plt.ylabel("Massa (g)")
plt.show()
plt.close('all')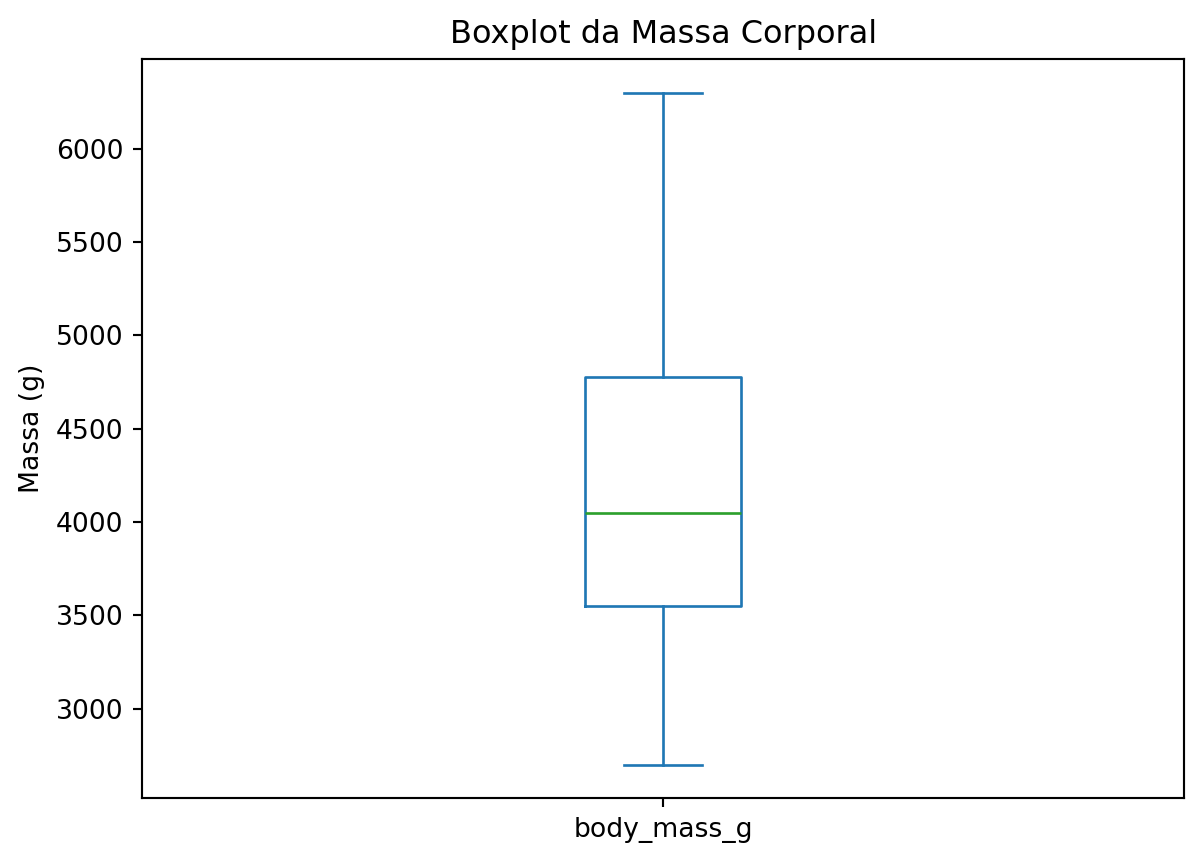

Nota

Interpretando boxplots:
- Linha central: mediana (Q2)
- Caixa: do Q1 ao Q3 (50% dos dados centrais)
- Whiskers: extensão até ~1.5 × IQR
- Pontos isolados: possíveis outliers

6 Medidas de Tendência Central

penguins['body_mass_g'].mean()    # Média aritmética
penguins['body_mass_g'].median()  # Mediana

np.float64(4050.0)

Dica

Quando usar cada medida:
- Média: dados simétricos, sem outliers extremos
- Mediana: dados assimétricos ou com outliers

7 Medidas de Variação

penguins['body_mass_g'].std()   # Desvio padrão
penguins['body_mass_g'].var()   # Variância

np.float64(648372.4876985418)

7.1 Cálculo manual da variância

x = penguins['body_mass_g']
# Fórmula: Σ(xi - x̄)² / (n-1)
variancia_manual = np.sum((x - x.mean())**2) / (len(x) - 1)
print(f"Variância manual: {variancia_manual}")
print(f"Variância pandas: {x.var()}")

Variância manual: 648372.4876985418
Variância pandas: 648372.4876985418

8 Escore-Z (Padronização)

A padronização transforma os dados para média = 0 e desvio padrão = 1:

\[Z = \frac{(X - \mu)}{\sigma}\]

media = penguins['body_mass_g'].mean()
desvio_padrao = penguins['body_mass_g'].std()

penguins['zscore_massa'] = (penguins['body_mass_g'] - media) / desvio_padrao

8.1 Verificando a padronização

penguins[['body_mass_g', 'zscore_massa']].head()

	body_mass_g	zscore_massa
0	3750.0	-0.567621
1	3800.0	-0.505525
2	3250.0	-1.188572
4	3450.0	-0.940192
5	3650.0	-0.691811

penguins[['body_mass_g', 'zscore_massa']].describe()

	body_mass_g	zscore_massa
count	333.000000	3.330000e+02
mean	4207.057057	-8.535048e-17
std	805.215802	1.000000e+00
min	2700.000000	-1.871619e+00
25%	3550.000000	-8.160012e-01
50%	4050.000000	-1.950496e-01
75%	4775.000000	7.053301e-01
max	6300.000000	2.599232e+00

Nota

Interpretação do Z-score:
- Z = 0: valor igual à média
- Z = 1: um desvio padrão acima da média
- Z = -1: um desvio padrão abaixo da média
- |Z| > 2: valor considerado incomum

9 Comparação Visual: Original vs Padronizado

fig, axes = plt.subplots(2, 1, figsize=(8, 6))

# Histograma da variável original
axes[0].hist(penguins['body_mass_g'], bins=20, color='skyblue', edgecolor='black')
axes[0].set_title("Massa Corporal (g) - Original")
axes[0].set_xlabel("Massa (g)")
axes[0].set_ylabel("Frequência")

# Histograma da variável padronizada
axes[1].hist(penguins['zscore_massa'], bins=20, color='lightgreen', edgecolor='black')
axes[1].set_title("Massa Corporal - Z-Score")
axes[1].set_xlabel("Escore-Z")
axes[1].set_ylabel("Frequência")

plt.tight_layout()
plt.show()
plt.close('all')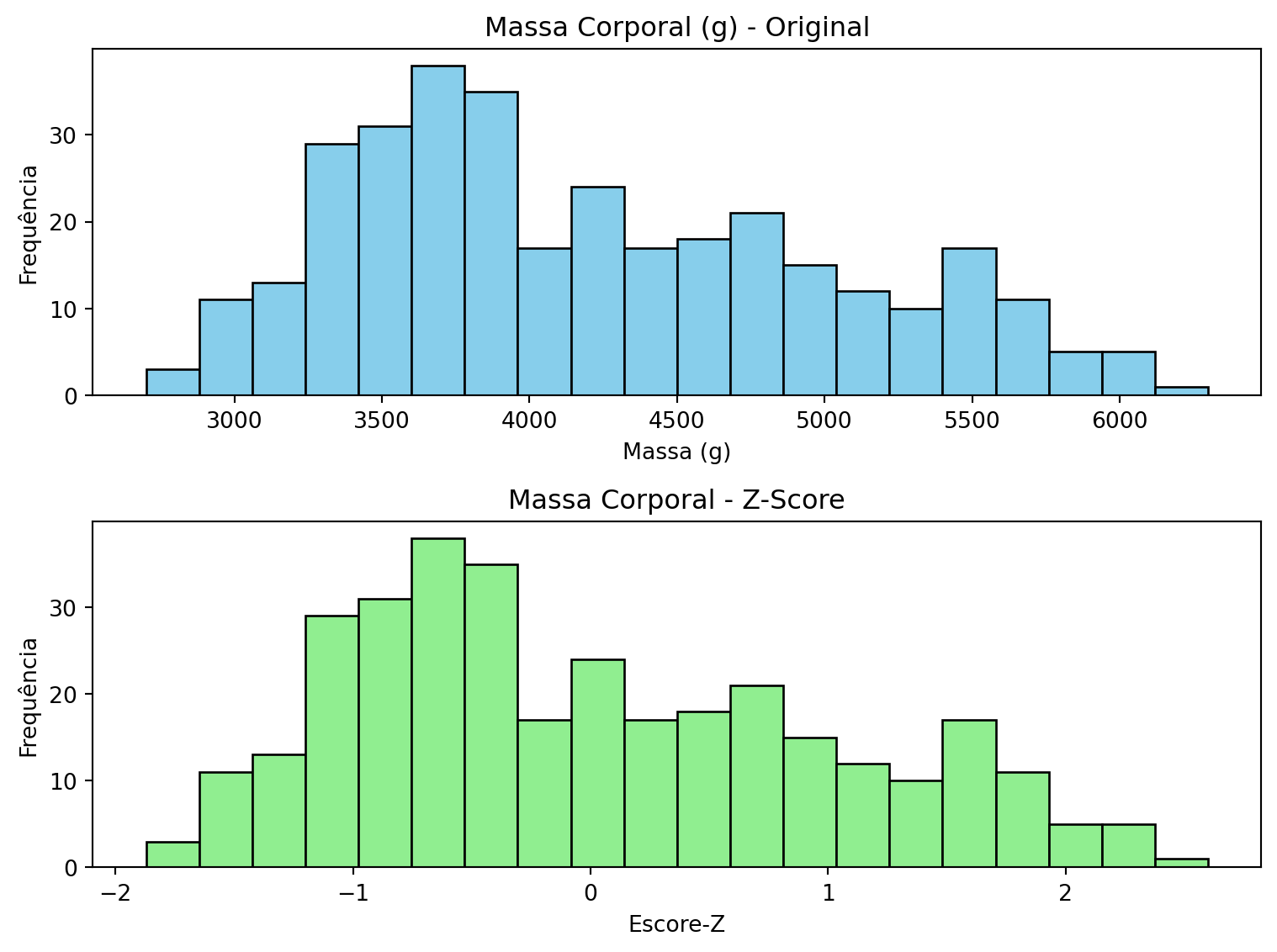

10 Resumo das Medidas

Medida	Função Python	Interpretação
Média	`.mean()`	Valor central (sensível a outliers)
Mediana	`.median()`	Valor central (robusta a outliers)
Desvio Padrão	`.std()`	Dispersão dos dados
Variância	`.var()`	Dispersão ao quadrado
Q1, Q3	`.quantile(0.25)`, `.quantile(0.75)`	Quartis
Mínimo/Máximo	`.min()`, `.max()`	Valores extremos

11 Aplicações Práticas

11.1 Identificando outliers com Z-score

# Valores com |Z| > 2 são considerados incomuns
outliers = penguins[np.abs(penguins['zscore_massa']) > 2]
print(f"Encontrados {len(outliers)} possíveis outliers")
outliers[['species', 'body_mass_g', 'zscore_massa']]

Encontrados 9 possíveis outliers

	species	body_mass_g	zscore_massa
165	Gentoo	5850.0	2.040376
167	Gentoo	5850.0	2.040376
169	Gentoo	6300.0	2.599232
185	Gentoo	6050.0	2.288757
229	Gentoo	6000.0	2.226661
231	Gentoo	5950.0	2.164566
263	Gentoo	5950.0	2.164566
267	Gentoo	5850.0	2.040376
269	Gentoo	6000.0	2.226661

11.2 Comparação rápida entre variáveis

# Estatísticas descritivas para múltiplas variáveis
colunas_numericas = ['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']
penguins[colunas_numericas].describe()

	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g
count	333.000000	333.000000	333.000000	333.000000
mean	43.992793	17.164865	200.966967	4207.057057
std	5.468668	1.969235	14.015765	805.215802
min	32.100000	13.100000	172.000000	2700.000000
25%	39.500000	15.600000	190.000000	3550.000000
50%	44.500000	17.300000	197.000000	4050.000000
75%	48.600000	18.700000	213.000000	4775.000000
max	59.600000	21.500000	231.000000	6300.000000