Modelo Normal Bayesiano

Modelando Dados Contínuos no PyMC - distribuições a priori

Introdução à modelagem Bayesiana de dados contínuos, incluindo escolha das priores e checagens preditivas.

Exploraremos a inferência bayesiana, com foco na modelagem de dados contínuos por meio da distribuição normal. Nosso objetivo será desenvolver a intuição sobre como escolher distribuições a priori e como o PyMC nos auxilia a visualizar as consequências dessas escolhas sobre a distribuição preditiva a priori da variável de interesse. Para isso, utilizaremos um exemplo baseado na distribuição de altura em adultos.

Objetivos de Aprendizagem

Apresentar e compreender a distribuição normal de forma intuitiva.
Simular dados a partir de distribuições normais utilizando scipy.
Utilizar seu conhecimento subjetivo para propor e visualizar distribuições a priori para os parâmetros de um modelo normal (por exemplo, altura de adultos).
Visualizar a distribuição preditiva a priori da variável resposta com o PyMC.

# Configuração inicial e importação de bibliotecas
import pymc as pm
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats

# Configurações para plots
plt.style.use('seaborn-v0_8-darkgrid')
plt.rcParams['figure.figsize'] = (9, 6)

1 Explorando a Distribuição Normal

A Distribuição Normal, frequentemente chamada de curva de sino ou curva Gaussiana, é central em estatística. Ela é caracterizada por dois parâmetros: a média (\(\mu\)) e o desvio padrão (\(\sigma\)). A média determina o centro da distribuição, enquanto o desvio padrão determina sua dispersão ou largura. Muitos fenômenos naturais podem ser adequadamente descritos por essa distribuição.

A ideia intuitiva: Pense na altura de adultos. Há um valor central (a média) em torno do qual a maioria das alturas se agrupa. Há também uma variação: algumas pessoas são mais altas, outras mais baixas. O desvio padrão nos diz o quão espalhadas essas alturas tendem a ser em relação à média.

1.1 Curva de densidade de probabilidade

Gerando a Distribuição de Densidade Normal para diferentes valores de \(\mu\) e \(\sigma\).

# Parâmetros da distribuição
mu_1 = 20
sigma_1 = 3

mu_2 = 20
sigma_2 = 6

mu_3 = 30
sigma_3 = 5

# Limites gráficos
x_min = np.min(np.array([mu_1, mu_2, mu_3]) - 4*np.array([sigma_1, sigma_2, sigma_3]))
x_max = np.max(np.array([mu_1, mu_2, mu_3]) + 4*np.array([sigma_1, sigma_2, sigma_3]))
x = np.linspace(x_min, x_max, 1000) # Faixa de alturas para plotar

pdf_1 = stats.norm.pdf(x, loc=mu_1, scale=sigma_1)
pdf_2 = stats.norm.pdf(x, loc=mu_2, scale=sigma_2)
pdf_3 = stats.norm.pdf(x, loc=mu_3, scale=sigma_3)

Visualizando as distribuições de densidade de probabilidade

plt.plot(x, pdf_1, label=f'$\mu={mu_1}, \sigma={sigma_1}$', color='b', lw=2)
plt.plot(x, pdf_2, label=f'$\mu={mu_2}, \sigma={sigma_2}$', color='r', lw=2)
plt.plot(x, pdf_3, label=f'$\mu={mu_3}, \sigma={sigma_3}$', color='g', lw=2)
plt.xlabel('X', fontsize=12)
plt.ylabel('Densidade de Probabilidade', fontsize=12)
plt.legend()
plt.grid(True, linestyle='-', alpha=0.7)
plt.show()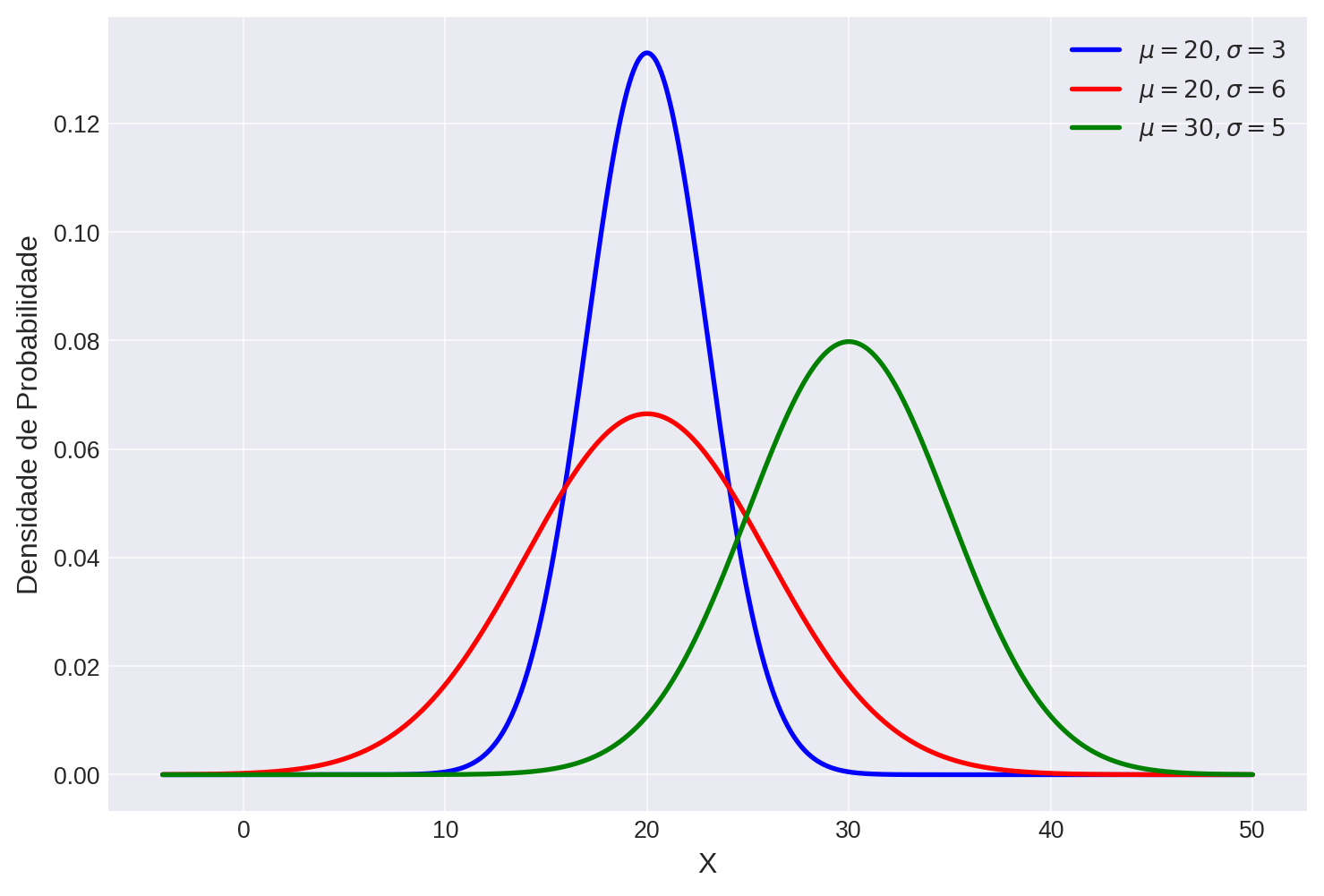

Figura 1: Desidades da distribuição normal para diferentes valores de μ e σ.

1.2 Amostrando valores de distribuição normal

Na Figura 1 vemos as curvas teóricas de densidade da distribuiçao normal. Podemos também gerar amostras valores ao acaso destas distribuições para verificar como estas amostras se parecem. Isso simula o processo de sortear alturas de uma população que segue essa distribuição.

mu = 20
sigma = 4
num_amostras = 60

Verificando o histograma dos valores sorteados.

amostras_y = stats.norm.rvs(loc=mu, scale=sigma, size=num_amostras)
x_dens = np.linspace(mu-4*sigma, mu+4*sigma, 500)

plt.hist(amostras_y, bins=30, density=True, alpha=0.8, color='lightblue', label='Amostras Geradas')
sns.kdeplot(amostras_y, color='blue', linewidth=2, label='Densidade Empírica')
plt.plot(x_dens, stats.norm.pdf(x_dens, loc=mu, scale=sigma), color='red', linewidth=2.5, label='Densidade Teórica')
plt.xlabel('X', fontsize=12)
plt.ylabel('Densidade / Frequência Normalizada', fontsize=12)
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()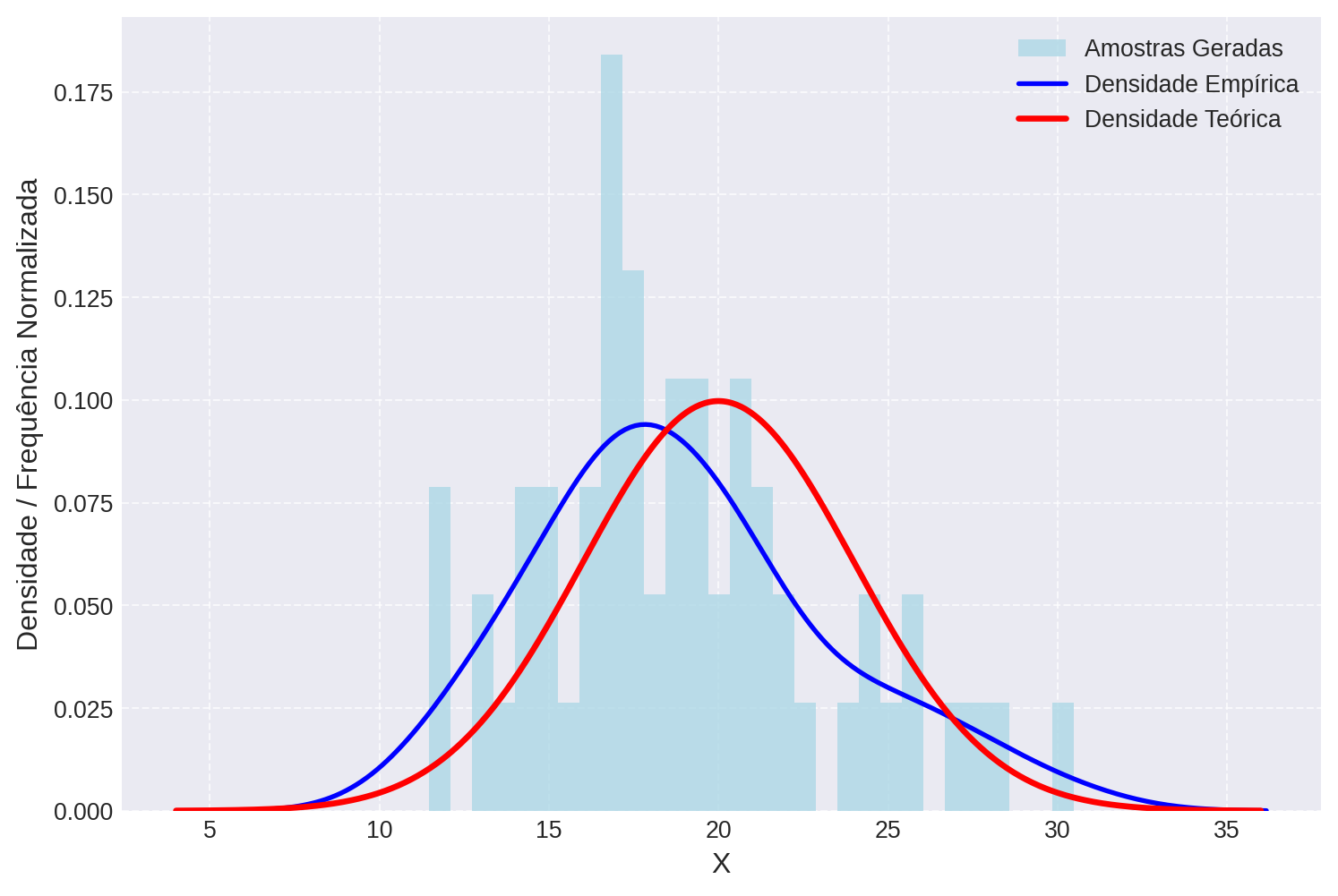

Figura 2: Histograma de amostras geradas a partir de uma distribuição normal com média \(\mu\) e desvio padrão \(\sigma\), acompanhado da densidade empírica estimada por kernel e da densidade teórica correspondente.

Atividade em laboratório

Rode este o trecho de código acima algumas vezes e observe como se dá a variação amostral.
Aumente e diminua o tamanho da amostras e verifique a variação entre as curvas enpíricas e a curva teórica.

2 Intuição Bayesiana

Em inferência Bayesiana, começamos com crenças sobre os parâmetros (a priori) e as atualizamos com dados (a posteriori). Para a altura humana (\(y\)), podemos assumir que a distribuição normal é um bom modelo preditivo.

Deste modo, escrevemos que:

\[y \sim \mathcal{N}(\mu, \sigma) \tag{1}\]

Em seguida, precisamos sugerir uma dristribuição a priori para a média \(\mu\) e o desvio padrão \(\sigma\) que traduzam de forma adequada o que esperamos sobre a distribuição de altura em adultos. Sabemos por exemplo que a média da altura de adultos não é 50 cm nem 300 cm. Qual sua intuição sobre o desvio padrão?

Atividade em laboratório

Assumindo que a distribuição de alturas em adultos segue uma dsitribuição normal proponha valores razoáveis para a média (\(\mu\)) e o desvio padrão (\(\sigma\)).
Para ajudar a decidir sobre o que seriam valores valores razoáveis, plote as curvas de densidade de probabilidade resultante de sua escolha e faça algumas simulações para verificar quais valores estremos sua escolha é capaz de gerar, utilizando os códigos da Seção 1.2.

2.1 Checagem Priori Preditiva

Assumindo que a altura de adultos segue uma distribuição (Equação 1), vamos assumir que o parâmetro \(\mu\) segue também uma distribuição normal e que \(\sigma\) segue uma distribuição log-normal

Como utilizamos estes pressupostos para escolher distribuição razoiáveis para \(\mu\) e \(\sigma\)?

Priori para \(\mu\)

mean_prior_mu =  # INSIRA SUA ESCOLHA PARA A MÉDIA DA PRIORI DE mu
sd_prior_mu =  # INSIRA SUA ESCOLHA PARA O DESVIO PADRÃO DA PRIORI DE mu

# Gere sequancia de x e calcule a PDF
xmean_prior = np.linspace(mean_prior_mu - 4*sd_prior_mu, mean_prior_mu + 4*sd_prior_mu, 1000)
pdf_mean_prior = stats.norm.pdf(x = xmean_prior, loc = mean_prior_mu, scale = sd_prior_mu)

# Plote os resultados
plt.plot(xmean_prior, pdf_mean_prior)
plt.title(f'Priori para $\mu$')
plt.show()

Priori para \(\sigma\)

lmean_prior_sigma =  # INSIRA SUA ESCOLHA PARA A MÉDIA DA PRIORI DE sigma
lsd_prior_sigma =  # INSIRA SUA ESCOLHA PARA O DESVIO PADRÃO DA PRIORI DE sigma

xsd_prior = np.linspace(0.01, 20, 1000)
pdf_sd_prior = stats.lognorm.pdf(xsd_prior, s=lsd_prior_sigma, scale=lmean_prior_sigma)

plt.close()
plt.plot(xsd_prior, pdf_sd_prior)
plt.title(f'Priori para $\sigma$')
plt.show()

Extraindo distribuição a priori preditiva de \(y\) no PyMC

# Definindo o modelo APENAS com as priores compartilhadas
with pm.Model() as prior_predictive_model:
    
    # Priori para a média
    mu = pm.Normal("mu", mu = mean_prior_mu, sigma = sd_prior_mu)

    # Priori lognormal para o desvio padrão
    sigma = pm.Lognormal("sigma", mu = np.log(lmean_prior_sigma), sigma = lsd_prior_sigma)

    # Distribuição preditiva de y
    y_pred = pm.Normal("y_pred", mu = mu, sigma = sigma)

    # Amostras da priori preditiva
    prior_predictive_samples = pm.sample_prior_predictive(samples=1000)

Agora, vamos visualizar a distribuição dessas amostras preditivas a priori:

y_pred_prior = prior_predictive_samples.prior["y_pred"].values.flatten()

plt.figure(figsize=(10, 6))
plt.hist(y_pred_prior, color='skyblue', edgecolor='black')
plt.xlabel('Alturas priori simulada (cm)', fontsize=12)
plt.ylabel('Densidade', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()

Figura 3

Discussão

Olhe para o histograma. As alturas simuladas parecem razoáveis para alturas de adultos? A distribuição faz sentido dada a sua intuição? Se sim, suas priores iniciais eram sensatas. Se não, é importante considerar um ajuste de suas priores (ex: tornar a priori de \(\sigma\) mais restrita se a dispersão for muito grande, ou ajustar a localização/escala da priori de \(\mu\)).

Checagem priori preditiva com PyMC

Podemos chegar não somente a distribuição preditiva de \(y\), mas também dos parâmetros \(\mu\) e \(\sigma\) usando o PyMC. Além disso, poderíamos testar outras distribuições a priori para algum dos parâmetros, por exemplo sigma. Teste cada uma destas e verifique os efeitos sobre as distribuições preditivas.

# Definindo o modelo APENAS com as priores compartilhadas
with pm.Model() as prior_predictive_model:
    
    # Priori para a média
    mu = pm.Normal("mu", mu=175, sigma=10)

    # Escolha uma das prioris para sigma:
    sigma = pm.Lognormal("sigma", mu=np.log(0.08), sigma=0.5)
    # sigma = pm.InverseGamma("sigma", alpha=8, beta=0.9)
    # sigma = pm.HalfNormal("sigma", sigma=0.1)
    # sigma = pm.HalfCauchy("sigma", beta=0.1)
    # sigma = pm.Exponential("sigma", lam=20)
    # sigma = pm.TruncatedNormal("sigma", mu=0.08, sigma=0.02, lower=0)
    # sigma = pm.Uniform("sigma", lower=0, upper=1)

    # Distribuição preditiva de y
    y_pred = pm.Normal("y_pred", mu=mu, sigma=sigma)

    # Amostras da priori preditiva
    prior_predictive_samples = pm.sample_prior_predictive(samples=1000)

mu_pred_prior = prior_predictive_samples.prior["mu"].values.flatten()
sigma_pred_prior = prior_predictive_samples.prior["sigma"].values.flatten()
y_pred_prior = prior_predictive_samples.prior["y_pred"].values.flatten()

fig, axes = plt.subplots(1, 3, figsize=(9, 3))

axes[0].hist(mu_pred_prior, bins=30, color='skyblue', edgecolor='black')
axes[0].set_xlabel("μ")
axes[0].set_ylabel("Frequência")

axes[1].hist(sigma_pred_prior, bins=30, color='lightgreen', edgecolor='black')
axes[1].set_xlabel("σ")
axes[1].set_ylabel("Frequência")

axes[2].hist(y_pred_prior, bins=30, color='salmon', edgecolor='black')
axes[2].set_xlabel("alturas (y)")
axes[2].set_ylabel("Frequência")

plt.tight_layout()
plt.show()

Figura 4