Construindo um modelo bayesiano
Verossimilhança e distribuição a priori
Construção de um modelo bayesiano, enfatizando a formulação de distribuições a priori e posterior. Baseado em Statistical Rethinking (McElreath 2018).
Considere um globo representando o planeta Terra, pequeno o suficiente para caber em suas mãos. Seu objetivo é estimar a fração da superfície coberta por água. Para isso, você adota a seguinte estratégia: joga o globo para cima girando e, ao pegá-lo, registra se o ponto tocado pelo seu dedo indicador direito é água (🌊) ou terra (🏜️). Você repete esse procedimento algumas vezes, obtendo uma sequência de \(n\) observações.
Você faz quatro lançamentos do globo e conta quantos deles resultam em água. Um possível resultado seria \(🌊🌊🏜️🌊\), totalizando 3 observações de água e 1 de terra. Outro resultado possível é \(🏜️🏜️🌊🌊\), com 2 observações de água e 2 de terra. Para \(n = 4\) observações, existem 16 resultados possíveis (Tabela 1).
| Nº | Dados | Nº pontos na água | Proporção de pontos na água |
|---|---|---|---|
| 1 | 🏜️ 🏜️ 🏜️ 🏜️ | 0 | 0/4 = 0.00 |
| 2 | 🏜️ 🏜️ 🏜️ 🌊 | 1 | 1/4 = 0.25 |
| 3 | 🏜️ 🏜️ 🌊 🏜️ | 1 | 1/4 = 0.25 |
| 4 | 🏜️ 🌊 🏜️ 🏜️ | 1 | 1/4 = 0.25 |
| 5 | 🌊 🏜️ 🏜️ 🏜️ | 1 | 1/4 = 0.25 |
| 6 | 🏜️ 🏜️ 🌊 🌊 | 2 | 2/4 = 0.50 |
| 7 | 🏜️ 🌊 🏜️ 🌊 | 2 | 2/4 = 0.50 |
| 8 | 🏜️ 🌊 🌊 🏜️ | 2 | 2/4 = 0.50 |
| 9 | 🌊 🏜️ 🏜️ 🌊 | 2 | 2/4 = 0.50 |
| 10 | 🌊 🏜️ 🌊 🏜️ | 2 | 2/4 = 0.50 |
| 11 | 🌊 🌊 🏜️ 🏜️ | 2 | 2/4 = 0.50 |
| 12 | 🏜️ 🌊 🌊 🌊 | 3 | 3/4 = 0.75 |
| 13 | 🌊 🏜️ 🌊 🌊 | 3 | 3/4 = 0.75 |
| 14 | 🌊 🌊 🏜️ 🌊 | 3 | 3/4 = 0.75 |
| 15 | 🌊 🌊 🌊 🏜️ | 3 | 3/4 = 0.75 |
| 16 | 🌊 🌊 🌊 🌊 | 4 | 4/4 = 1.00 |
Observe que apenas um dos resultados contém 4 observações de terra e somente um contém 4 observações de água. Os demais são variações entre esses extremos.
Podemos reorganizar a tabela para evidenciar todas as combinações que levam ao mesmo número \(y_i\) de pontos em água:
| Nº pontos na água (\(y_i\)) | Dados | Nº de combinações |
|---|---|---|
| 0 | 🏜️ 🏜️ 🏜️ 🏜️ | 1 |
| 1 | 🏜️ 🏜️ 🏜️ 🌊 🏜️ 🌊 🏜️ 🏜️ 🏜️ 🏜️ 🌊 🏜️ 🌊 🏜️ 🏜️ 🏜️ |
4 |
| 2 | 🏜️ 🏜️ 🌊 🌊 🏜️ 🌊 🏜️ 🌊 🏜️ 🌊 🌊 🏜️ 🌊 🏜️ 🏜️ 🌊 🌊 🏜️ 🌊 🏜️ 🌊 🌊 🏜️ 🏜️ |
6 |
| 3 | 🏜️ 🌊 🌊 🌊 🌊 🏜️ 🌊 🌊 🌊 🌊 🏜️ 🌊 🌊 🌊 🌊 🏜️ |
4 |
| 4 | 🌊 🌊 🌊 🌊 | 1 |
Defina \(p\) como a probabilidade de observar água e \(1 - p\) como a probabilidade de observar terra após cada lançamento do globo.
A última linha da Tabela 2 (🌊🌊🌊🌊) tem probabilidade: \[P(4) = p \times p \times p \times p.\]
Enquanto a primeira linha (🏜️🏜️🏜️🏜️) ocorre com probabilidade: \[P(0) = (1 - p) \times (1 - p) \times (1 - p) \times (1 - p).\]
As linhas correspondentes a \(P(1)\), \(P(2)\) e \(P(3)\) são combinações de \(p\) e \((1 - p)\), multiplicadas pelo número de formas pelas quais 1, 2 ou 3 registros de água podem ocorrer em 4 lançamentos.
| Nº pontos na água (\(y\)) | Dados | Nº de combinações | \(P(Y)\) |
|---|---|---|---|
| 0 | 🏜️ 🏜️ 🏜️ 🏜️ | 1 | \(1 \times (1-p) \times (1-p) \times (1-p) \times (1-p)\) |
| 1 | 🏜️ 🏜️ 🏜️ 🌊 🏜️ 🌊 🏜️ 🏜️ 🏜️ 🏜️ 🌊 🏜️ 🌊 🏜️ 🏜️ 🏜️ |
4 | \(4 \times p \times (1-p) \times (1-p) \times (1-p)\) |
| 2 | 🏜️ 🏜️ 🌊 🌊 🏜️ 🌊 🏜️ 🌊 🏜️ 🌊 🌊 🏜️ 🌊 🏜️ 🏜️ 🌊 🌊 🏜️ 🌊 🏜️ 🌊 🌊 🏜️ 🏜️ |
6 | \(6 \times p \times p \times (1-p) \times (1-p)\) |
| 3 | 🏜️ 🌊 🌊 🌊 🌊 🏜️ 🌊 🌊 🌊 🌊 🏜️ 🌊 🌊 🌊 🌊 🏜️ |
4 | \(4 \times p \times p \times p \times (1-p)\) |
| 4 | 🌊 🌊 🌊 🌊 | 1 | \(1 \times p \times p \times p \times p\) |
1 O modelo Binomial
A partir das expressões para \(P(y)\) apresentadas na Tabela 3, obtém-se uma fórmula geral que pode ser escrita como:
\[P(y \mid n, p) = \binom{n}{y} \, p^y (1 - p)^{n - y}. \tag{1}\]
Onde:
- \(y \in \{0, 1, 2, \dots, n\}\) é o número de observações de 🌊;
- \(n\) é o número total de observações;
- \(p\) é a fração de 🌊 que cobre o globo;
- \(\binom{n}{y}\) é o coeficiente binomial, calculado por \(\frac{n!}{y!(n - y)!}\), indicando de quantas maneiras a combinação \(p^y (1 - p)^{n - y}\) pode ocorrer.
A Equação 1 fornece a probabilidade de cada resultado possível (número de observações 🌊) em \(n\) tentativas, permitindo calcular a probabilidade de todos os possíveis resultados do experimento.
2 Verossimilhança: a plausibilidade de uma hipótese
A partir do modelo binomial, podemos definir a função de verossimilhança para um resultado observado. Imagine que, em \(n = 4\) lançamentos, foram observados \(y = 2\) pontos sobre a água. Não sabemos a verdadeira proporção \(p\) de água que cobre a Terra; portanto, fazemos conjecturas e avaliamos cada uma com base nas observações.
Por exemplo, se supormos que a proporção verdadeira seja 40% \((p = 0.4)\), a distribuição binomial determina que a probabilidade de observar \(y = 2\) sucessos em \(n = 4\) lançamentos seja:
\[P(y = 2 \mid n = 4, p = 0.4) = \binom{4}{2} \, 0.4^2 (1 - 0.4)^{4 - 2} = 0.35\]
Essa hipótese é apenas uma das possíveis. Para ilustrar outras conjecturas, considere:
Se \(p = 0.3\):
\(P(2 \mid 4, 0.3) = \binom{4}{2} \, 0.3^2 (1 - 0.3)^{4 - 2} = 0.26\)
Se \(p = 0.8\):
\(P(2 \mid 4, 0.8) = \binom{4}{2} \, 0.8^2 (1 - 0.8)^{4 - 2} = 0.15\)
Em cada caso, os dados observados \((y)\) e o número total de observações \((n)\) estão fixos, enquanto o parâmetro \(p\) varia conforme a hipótese considerada. Embora a forma matemática seja idêntica à da função de probabilidade binomial, seu uso é diferente. Na função de probabilidade, lemos a probabilidade de \(y\) dado \(n\) e \(p\), enquanto nos exemplos acima, avaliamos a plausibilidade de diferentes hipóteses sobre \(p\) dados valores fixos de \(y\) e \(n\).
Para evitar confusões, vamos definir a função de verossimilhança como:
\[ \mathcal{L}(p \mid n, y) = \binom{n}{y} \, p^y (1 - p)^{n - y}. \tag{2}\]
Assim, as verossimilhanças para as três conjecturas específicas sobre a proporção de água na superfície do globo serão:
- \(\mathcal{L}(p = 0.4 \mid n = 4, y = 2) = 0.35\),
- \(\mathcal{L}(p = 0.3 \mid n = 4, y = 2) = 0.26\),
- \(\mathcal{L}(p = 0.8 \mid n = 4, y = 2) = 0.15\).
Dessa forma, entre as três hipóteses levantadas, aquela em que \(p = 0.4\) recebe maior suporte das evidências, por estar associada à maior verossimilhança.
Podemos quantificar esse suporte por meio da razão de verossimilhanças:
\[RV = \frac{\mathcal{L}(p = 0.4 \mid 4, 2)}{\mathcal{L}(p = 0.3 \mid 4, 2)} = \frac{0.35}{0.26} = 1.35,\]
o que indica que, com base nos dados observados, a hipótese de \(p = 0.4\) é aproximadamente \(1.35\) vezes mais verossímil do que a hipótese de \(p = 0.3\).
AvisoResumo: A Função de Verossimilhança Binomial
- A expressão é matematicamente idêntica à função de probabilidade binomial, porém interpretada como uma função de \(p\) quando os dados \(Y\) e \(n\) são fixos.
- A verossimilhança indica a plausibilidade de diferentes valores de \(p\) à luz dos dados observados.
- Na distribuição binomial, lemos: probabilidade de \(Y\) dado \(n\) e \(p\).
- Na função de verossimilhança, interpretamos: verossimilhança de \(p\) dado \(n\) e \(Y\).
- A razão de verossimilhanças pode ser utilizada para quantificar o suporte relativo entre diferentes hipóteses.
2.1 O perfil de verossimilhança
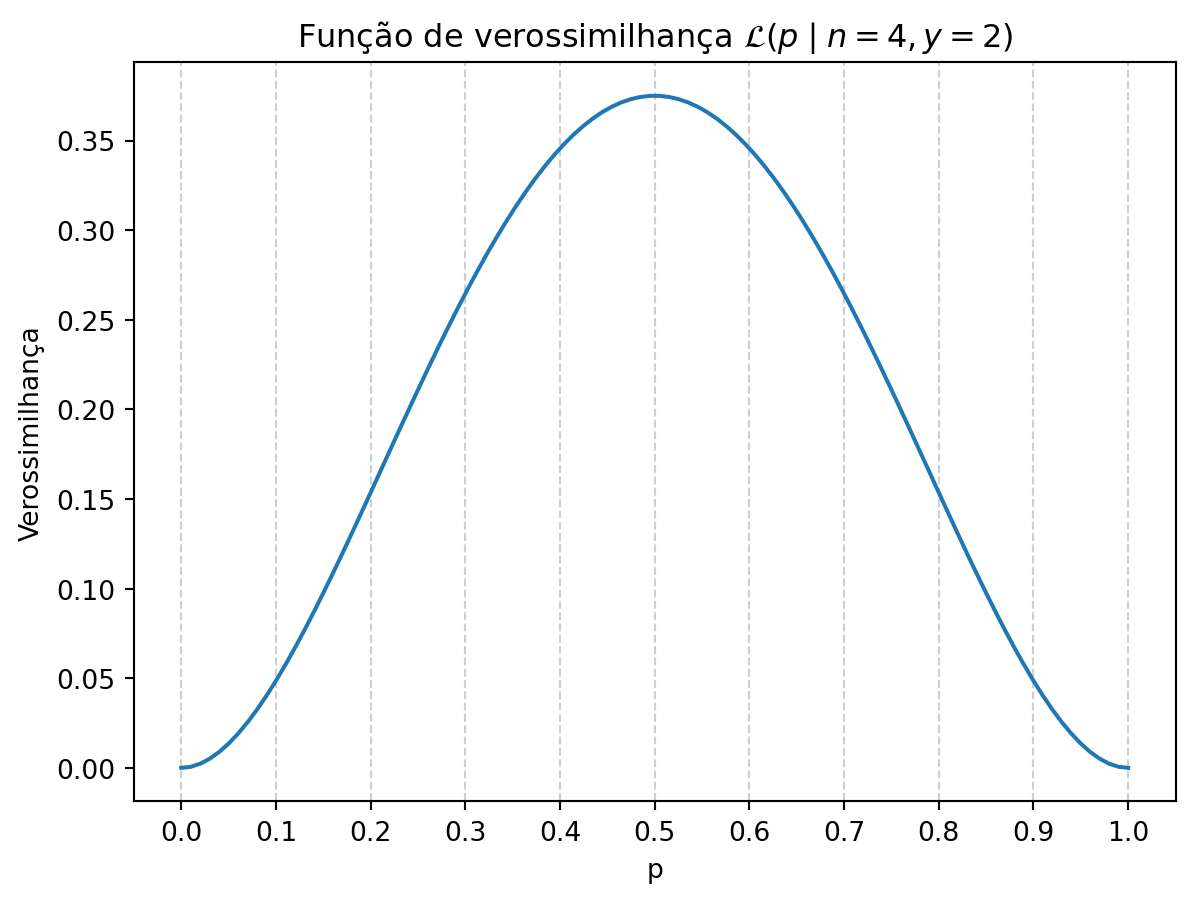
Acima, foram testadas três conjecturas específicas para a proporção de água na superfície da Terra (\(p = 0.3\), \(p = 0.4\), \(p = 0.8\)). Para uma avaliação mais completa, podemos analisar o perfil de verossimilhança para uma série de valores de \(p\) entre 0 e 1:
O perfil de verossimilhança indica que, à luz dos nossos dados \(y = 2\), a conjectura mais plausível é que a proporção de água que cobre a Terra esteja próxima de 0.5 (neste caso, a verossimilhança máxima é exatamente para \(p = 0.5\)).
3 Inferência Bayesiana: distribuições a priori e a posteriori
A inferência bayesiana utiliza o Teorema de Bayes para derivar a distribuição a posteriori dos parâmetros de interesse, \(p(\theta \mid Y)\), a partir da verossimilhança \(p(Y \mid \theta)\) e da distribuição a priori \(p(\theta)\):
\[p(\theta \mid Y) = \frac{p(Y \mid \theta) \times p(\theta)}{p(Y)} \tag{3}\]
Em que:
- \(p(\theta \mid Y)\): distribuição a posteriori de \(\theta\) dado os dados observados \(Y\);
- \(p(Y \mid \theta)\): verossimilhança dos dados \(Y\) dada \(\theta\);
- \(p(\theta)\): distribuição a priori de \(\theta\);
- \(p(Y)\): probabilidade marginal dos dados, obtida por
\[\int p(Y \mid \theta) \times p(\theta) \, d\theta\]
No contexto bayesiano, é comum substituir \(p(Y \mid \theta)\) pela função de verossimilhança \(\mathcal{L}(\theta \mid Y)\), pois ambas são matematicamente equivalentes. Assim, a fórmula da distribuição a posteriori pode ser reescrita como:
\[p(\theta \mid Y) = \frac{\mathcal{L}(\theta \mid Y) \times p(\theta)}{p(Y)} \tag{4}\]
4 Priori informativa e não informativa
Denominamos priori não informativa aquela que não acrescenta informações relevantes à distribuição a posteriori além daquelas já contidas nos dados observados. Nesses casos, a distribuição a posteriori é proporcional apenas à verossimilhança:
\[p(\theta \mid Y) \propto \mathcal{L}(\theta \mid Y) \tag{5}\]
Por outro lado, ao adotarmos uma priori informativa, atribuímos diferentes densidades de probabilidade às regiões específicas do espaço de parâmetros, refletindo o conhecimento prévio sobre o fenômeno estudado. A distribuição a posteriori, nesse caso, será proporcional ao produto entre a verossimilhança e a priori, integrando evidências anteriores com a informação contida nos dados:
\[p(\theta \mid Y) \propto \mathcal{L}(\theta \mid Y) \times p(\theta) \tag{6}\]
No modelo binomial aplicado à proporção de água na superfície oceânica, o parâmetro \(\theta\) representa a proporção de água \(p\), e sua distribuição posterior é condicional ao número de observações \(n\) e aos dados observados \(y\).
A distribuição a priori para \(p\) pode ser não informativa, como no caso da distribuição uniforme, que não favorece nenhum valor específico de \(p\). Alternativamente, pode-se adotar uma priori informativa, como a distribuição Beta, que permite ajustar a forma da densidade de probabilidade por meio dos parâmetros \(\alpha\) e \(\beta\), incorporando conhecimento prévio sobre o fenômeno de interesse.
Para ilustrar o efeito de prioris informativas e não-informativas sobre a distribuição a posteriori, siga a atividade abaixo:
DicaAtividades interativas: estimando a proporção da superfície oceânica!
Amostre pontos no globo e faça sua própria inferência bayesiana
No app abaixo, gere pontos aleatórios na superfície da Terra e verifique quantos caem em água ou em terra.👉 Estimando a Proporção da Superfície Oceânica
- Escolha quantos pontos deseja amostrar (1 a 1000).
- Clique em “Gerar Pontos Aleatórios” e observe quantos ficam sobre a água versus sobre a terra.
- Registre esses valores como \(k\) sucessos em \(N\) pontos (N observações).
- Escolha quantos pontos deseja amostrar (1 a 1000).
Utilize seus dados na inferência Bayesiana
Em seguida, abra o app abaixo para visualizar como as observações (sucessos e fracassos) combinadas a diferentes escolhas de parâmetros a priori (\(\alpha\), \(\beta\)) geram a distribuição a posteriori:Dicas de uso
- Insira o mesmo número de observações (N) e sucessos (k) obtidos no primeiro app.
- Ajuste interativamente a distribuição a priori Beta, modificando os parâmetros \(\alpha\) e \(\beta\).
- Observe como a curva azul (“posteriori”) se altera de acordo com a a priori e com os dados observados, e compare com o perfil de verossimilhança (curva verde).
- Note que ao escolher \(\alpha = 1\) e \(\beta = 1\) a distribuição assume um formato uniforme, tornando-se não-informativa.
- Insira o mesmo número de observações (N) e sucessos (k) obtidos no primeiro app.
Referências
McElreath, Richard. 2018. Statistical rethinking: A Bayesian course with examples in R and Stan. Chapman; Hall/CRC.