Contando possibilidades
Evidências sobre uma hipótese
A inferência bayesiana, em essência, é uma forma de contar e comparar as diferentes maneiras pelas quais algo pode acontecer. A seguir, vamos desenvolver os princípios da inferência bayesiana de forma simples e intuitiva utilizando o princípio da contagem.
Imagine que temos uma caixa contendo quatro bolinhas de gude, que podem ser azuis ou brancas. Sabemos que há exatamente quatro bolinhas, mas não conhecemos a distribuição entre as cores. Com base nessa informação, podemos listar cinco configurações possíveis:
- [⚪⚪⚪⚪]
- [🔵⚪⚪⚪]
- [🔵🔵⚪⚪]
- [🔵🔵🔵⚪]
- [🔵🔵🔵🔵]
Essas são todas as possibilidades compatíveis com o que sabemos sobre o conteúdo da caixa — o conhecimento a priori. Chamamos essas cinco configurações de hipóteses.
Nosso objetivo será descobrir qual dessas hipóteses é mais plausível à medida que obtivermos evidências sobre o conteúdo da caixa.
1 Um leque de possibilidades
A caixa possui um orifício pelo qual podemos ver apenas uma bolinha por vez. Assim, a única forma de obter evidências sobre o conteúdo da caixa será fazer uma observação, misturar as bolinhas, fazer outra observação e assim por diante. Antes de iniciar esse processo, vamos entender como cada observação nos ajuda a alcançar nosso objetivo, avaliando-as à luz das hipóteses sobre o conteúdo da caixa.
Vamos começar assumindo que seja verdadeira a situação (2) [🔵⚪⚪⚪]. Nesse caso, teríamos 1 possibilidade de observar a bolinha azul e 3 possibilidades de observar uma bolinha branca (Figura 1).
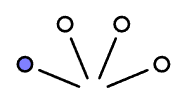
Observe que, embora as três bolinhas brancas pareçam iguais do ponto de vista dos dados (pois apenas registramos suas cores), elas são eventos diferentes. Isso é importante, pois significa que há três maneiras a mais de observar ⚪ do que 🔵.
Observamos agora uma segunda bolinha. Isso expande nosso leque de possibilidades em mais uma camada (Figura 2). Agora existem 16 caminhos possíveis (um para cada par de observações), pois, na segunda observação, cada um dos caminhos anteriores se ramifica em outros quatro caminhos possíveis.
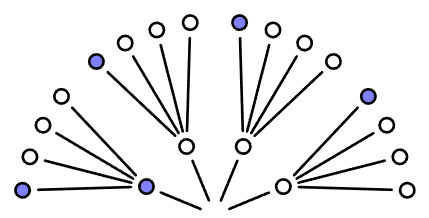
Ao observar uma terceira bolinha da caixa, a terceira camada é construída da mesma forma, e agora temos \(4^3 = 64\) caminhos possíveis para uma sequência de observações de cores em uma caixa com 4 bolinhas (Figura 3).
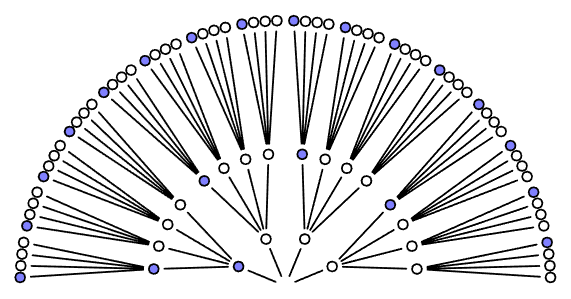
Acreditamos que, ao sacudir a caixa, cada bolinha tem a mesma chance de ser observada pelo orifício, independentemente de qual tenha saído anteriormente. Por isso, cada caminho do leque é igualmente provável de ser observado.
2 Avaliando as evidências
À medida que observamos a cor de uma nova bolinha da caixa, alguns desses caminhos são logicamente eliminados.
Suponha que a sequência de cores observada tenha sido:
1ª bolinha: 🔵
2ª bolinha: ⚪
3ª bolinha: 🔵
Após a primeira retirada resultar em 🔵, os três caminhos que levariam à observação de uma bolinha branca na primeira camada são imediatamente eliminados. Na segunda retirada, obtivemos ⚪, de modo que um dos caminhos possíveis na segunda camada foi eliminado, restando os três caminhos que se ramificam a partir do primeiro caminho azul. Após a terceira observação, cada um dos três caminhos restantes na segunda camada segue somente para a bolinha azul na terceira camada. Assim, assumindo que a caixa contenha [🔵⚪⚪⚪], existe um total de três maneiras para a sequência [🔵 → ⚪ → 🔵] aparecer. Todas as outras possibilidades foram descartadas à medida que as evidências surgiam.
Dos caminhos restantes na Figura 4, não podemos ter certeza de qual dos três caminhos os dados reais seguiram, pois não podemos identificar as bolinhas individualmente, apenas por sua cor. Entretanto, considerando a hipótese de que a caixa contenha [🔵⚪⚪⚪], podemos afirmar que os dados seguiram um desses três caminhos, pois são os únicos compatíveis tanto com nosso conhecimento prévio (4 bolinhas, azuis ou brancas) quanto com a sequência de dados observada ([🔵 → ⚪ → 🔵]).
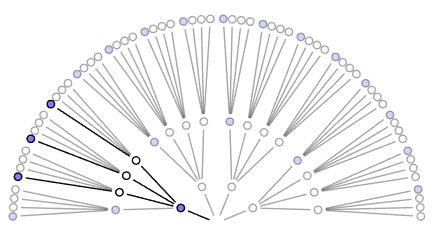
3 Avaliando as demais hipóteses
Considerando que a caixa contenha [🔵⚪⚪⚪], verificamos que apenas três dos 64 caminhos possíveis poderiam gerar a sequência [🔵 → ⚪ → 🔵]. Falta agora aplicar a mesma lógica às demais hipóteses. Por exemplo, considere [⚪⚪⚪⚪]. Há zero maneiras de essa hipótese produzir os dados observados, pois uma única 🔵 já é logicamente incompatível com ela. A hipótese [🔵🔵🔵🔵] também não pode produzir a sequência, pois há ao menos uma ⚪ observada. Assim, podemos eliminar essas duas hipóteses, pois nenhuma delas fornece sequer um único caminho consistente com os dados.
Para as hipóteses restantes, isto é, [🔵🔵⚪⚪] e [🔵🔵🔵⚪], o leque de possibilidades se abre novamente.
A Figura 5 mostra o leque completo para as três hipóteses compatíveis com os dados observados: [🔵⚪⚪⚪], [🔵🔵⚪⚪] e [🔵🔵🔵⚪].
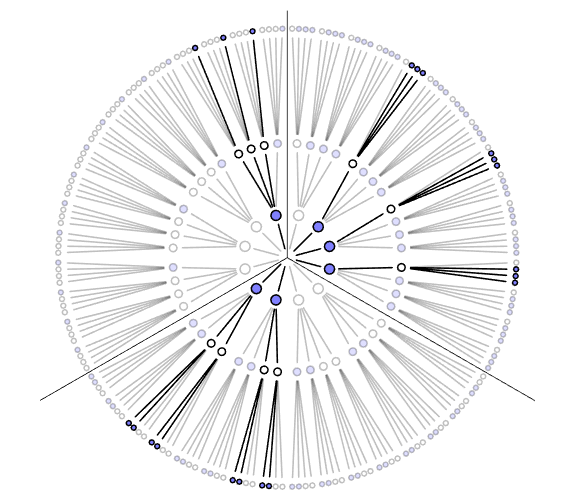
Agora, contamos todas as maneiras pelas quais cada hipótese poderia produzir os dados observados. Para uma bolinha azul e três brancas, existem três maneiras (como já contamos). Para duas bolinhas azuis e duas brancas, há oito caminhos consistentes com a sequência. Para três bolinhas azuis e uma branca, há nove caminhos que sobrevivem às observações.
Consideramos, assim, as cinco hipóteses diferentes sobre o conteúdo da caixa, variando de zero bolinhas 🔵 a quatro bolinhas 🔵 e, para cada uma dessas hipóteses, contamos quantas possibilidades (ou “caminhos”) poderiam potencialmente produzir a sequência observada.
| Hipótese | Maneiras de produzir [🔵 → ⚪ → 🔵] |
|---|---|
| 1. [⚪⚪⚪⚪] | \(0 \times 4 \times 0 = 0\) |
| 2. [🔵⚪⚪⚪] | \(1 \times 3 \times 1 = 3\) |
| 3. [🔵🔵⚪⚪] | \(2 \times 2 \times 2 = 8\) |
| 4. [🔵🔵🔵⚪] | \(3 \times 1 \times 3 = 9\) |
| 5. [🔵🔵🔵🔵] | \(4 \times 0 \times 4 = 0\) |
Observe que o número de maneiras de produzir os dados, para cada hipótese, pode ser obtido contando as ramificações em cada camada do leque de possibilidades e, em seguida, multiplicando esses valores (Tabela 1). Isso é apenas um recurso computacional. Ele nos diz a mesma coisa que a Figura 5, mas sem precisar desenhar todo o diagrama. O fato de multiplicarmos os números não altera o sentido de estarmos apenas contando caminhos logicamente possíveis.
4 Atualizando o conhecimento
Suponha que o experimento anterior, sumarizado na Tabela 1, tenha sido finalizado. Isso nos diz que, por ora, temos evidências melhores para as hipóteses 3 e 4, isto é, de que a caixa contenha 2 ou 3 bolinhas azuis. Para ajudar a diferenciar essas duas possibilidades ainda mais, resolvemos continuar o experimento e amostrar outra bolinha, o que resultou na observação de uma bolinha azul. Como se trata de um novo experimento, poderíamos recomeçar todo o processo. No entanto, há uma forma melhor de aproveitar o conhecimento adquirido a priori — para cada hipótese, listamos as maneiras anteriores de produzir as observações (o prior) e multiplicamos pelo número de maneiras de produzir a nova evidência 🔵:
| Hipótese | Contagem anterior (prior) | Maneiras de produzir a nova observação 🔵 | Contagem posterior |
|---|---|---|---|
| 1. [⚪⚪⚪⚪] | 0 | 0 | \(0 \times 0 = 0\) |
| 2. [🔵⚪⚪⚪] | 3 | 1 | \(3 \times 1 = 3\) |
| 3. [🔵🔵⚪⚪] | 8 | 2 | \(8 \times 2 = 16\) |
| 4. [🔵🔵🔵⚪] | 9 | 3 | \(9 \times 3 = 27\) |
| 5. [🔵🔵🔵🔵] | 0 | 4 | \(0 \times 4 = 0\) |
A nova contagem na coluna da direita da Tabela 2 resume as evidências a favor de cada hipótese, de modo que sejam compatíveis tanto com as observações anteriores quanto com a nova observação. Portanto, à medida que novos dados chegam e, desde que sejam independentes dos anteriores, o total de caminhos logicamente possíveis para explicar tanto as observações antigas quanto as novas pode ser calculado pela multiplicação das contagens anteriores pelas novas.
Em outras palavras, sempre que temos \(W_\text{prior}\) maneiras de uma hipótese produzir observações anteriores (\(D_\text{prior}\)) e, em seguida, obtemos novas observações (\(D_\text{novo}\)) que essa mesma hipótese pode produzir de \(W_\text{novo}\) maneiras, a quantidade total de formas possíveis para essa hipótese explicar tanto os dados antigos quanto os novos é dada simplesmente por \(W_\text{prior} \times W_\text{novo}\). Por exemplo, na Tabela 2, a hipótese [🔵🔵⚪⚪] apresenta \(W_\text{prior} = 8\) maneiras de gerar as observações anteriores [🔵 → ⚪ → 🔵] e \(W_\text{novo} = 2\) maneiras de gerar a nova observação [🔵]. Logo, \(8 \times 2 = 16\) caminhos possíveis para explicar tanto os dados antigos quanto os novos.
No exemplo acima, os dados antigos e os novos são do mesmo tipo (bolinhas observadas na caixa). Entretanto, não há motivo para excluir a situação em que os dados antigos e os novos tenham sido obtidos de forma diferente. Suponha, por exemplo, que alguém da fábrica de bolinhas informe que as azuis são raras. Para cada caixa contendo [🔵🔵🔵⚪], a fábrica produz duas caixas contendo [🔵🔵⚪⚪] e três caixas contendo [🔵⚪⚪⚪]. Também garante que cada caixa contenha pelo menos uma bolinha azul e uma bolinha branca. Com essa nova informação, podemos atualizar nossas contagens novamente (Tabela 3).
| Hipótese | Contagem anterior (prior) | Maneiras de produzir 🔵 informadas pela fábrica | Nova contagem |
|---|---|---|---|
| 1. [⚪⚪⚪⚪] | 0 | 0 | \(0 \times 0 = 0\) |
| 2. [🔵⚪⚪⚪] | 3 | 3 | \(3 \times 3 = 9\) |
| 3. [🔵🔵⚪⚪] | 16 | 2 | \(16 \times 2 = 32\) |
| 4. [🔵🔵🔵⚪] | 27 | 1 | \(27 \times 1 = 27\) |
| 5. [🔵🔵🔵🔵] | 0 | 0 | \(0 \times 0 = 0\) |
Agora, à luz dessa informação adicional, a hipótese [🔵🔵⚪⚪] torna-se ligeiramente mais plausível do que [🔵🔵🔵⚪].