Teorema de Bayes

Teorema de Bayes
Probabilidade condicional
Eventos dependentes
Apresentação do Teorema de Bayes e sua aplicação no cálculo de probabilidades condicionais. 
source("scripts/conditional_tree.r")

O Teorema de Bayes provém da definição de probabilidade condicional:

\[P(B|A) = \frac{P(A \cap B)}{P(A)},\]

o que implica:

\[P(A \cap B) = P(A)\,P(B|A).\]

Podemos também escrever:

\[P(A|B) = \frac{P(A \cap B)}{P(B)}, \quad P(A \cap B) = P(B)\,P(A|B).\]

Como \(P(A \cap B) = P(B \cap A)\), segue:

\[P(A)\,P(B|A) = P(B)\,P(A|B),\]

resultando na forma geral do Teorema de Bayes:

\[P(B|A) = \frac{P(B)\,P(A|B)}{P(A)}.\]

1 Teorema da probabilidade total

Considere o esquema de um diagrama de árvore:

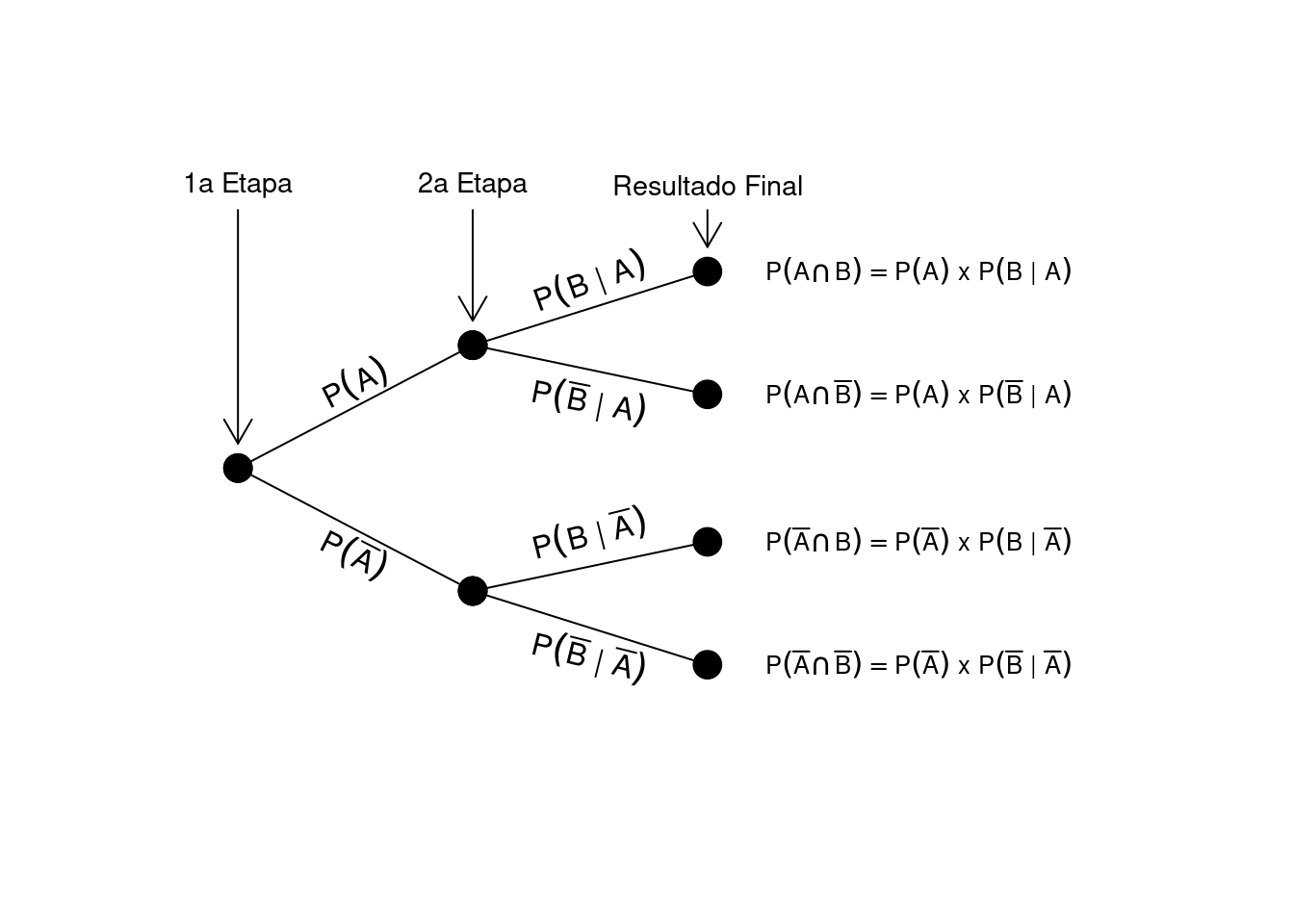
Dois caminhos podem levar à ocorrência de \(A\): um em que \(B\) ocorre \(\bigl[P(A \cap B)\bigr]\) e outro em que \(B\) não ocorre \(\bigl[P(A \cap \overline{B})\bigr]\). Por serem mutuamente exclusivos:

\[P(A) = P(A \cap B) + P(A \cap \overline{B}),\]

que pode ser reescrito como:

\[P(A) = P(B)\,P(A|B) + P(\overline{B})\,P(A|\overline{B}).\]

Este resultado é conhecido como Teorema da probabilidade total. Assim, o Teorema de Bayes pode ser expresso por:

\[ P(B|A) = \frac{P(B)\,P(A|B)}{P(B)\,P(A|B) + P(\overline{B})\,P(A|\overline{B})}. \]

2 O problema da detecção de espécies

Suponha um estudo sobre a presença de uma espécie de peixe em riachos costeiros da Mata Atlântica. Ela ocorre em 5% dos riachos \(\bigl[P(O) = 0,05\bigr]\), sendo, portanto, rara. A detecção se dá por captura e identificação taxonômica. Se a espécie está presente, a probabilidade de captura é \(0,99\), havendo \(0,01\) de falso negativo (quando a espécie não é detectada mesmo presente).

Há também a possibilidade de falso positivo: mesmo quando ausente, existe uma chance de 0,10 de a espécie ser registrada erroneamente, devido à semelhança com outra espécie presente na região.

Podemos organizar essas probabilidades em um diagrama de árvore:

Diagrama de árvore representando as probabilidades de ocorrência P(O) e detecção P(D) de uma espécie.

As ramificações mostram as bifurcações do evento “espécie presente ou ausente” e, em seguida, “detecção ou não-detecção”. Assim, são possíveis:

  • \(P(O \cap D) = 0,0495\)
  • \(P(O \cap \overline{D}) = 0,0005\)
  • \(P(\overline{O} \cap D) = 0,095\)
  • \(P(\overline{O} \cap \overline{D}) = 0,855\)

A probabilidade total de detecção \(P(D)\) é:

\[P(D) = P(O \cap D) + P(\overline{O} \cap D) = 0,0495 + 0,095 = 0,1445.\]

2.1 Razão de verossimilhança, inferência bayesiana e teste de hipóteses

Uma pergunta relevante é:

Ao sabermos de uma possível detecção, podemos ter certeza da presença dessa espécie?

Em inferência estatística, buscamos tomar decisões a respeito de um fenômeno desconhecido com base em dados observados. Aqui, exploramos duas abordagens: verossimilhança e inferência bayesiana.

2.1.1 Verossimilhança: uma medida indireta para \(P(O|D)\)

Se \(P(D|O)\) for alta, a presença da espécie se torna mais plausível, pois a chance de detectá-la quando está presente é elevada. Já \(P(D|\overline{O})\) alto indicaria que a não-ocorrência é mais provável, pois há muitos falsos positivos.

Em estatística, \(P(D|O)\) é análogo à verossimilhança de \(O\) dado \(D\). De modo simplificado, contrastamos duas hipóteses:

  • Espécie ocorre e é detectada;
  • Espécie não ocorre, mas há detecção falsa.

A razão de verossimilhança (\(RV\)) é:

\[RV = \frac{P(D|O)}{P(D|\overline{O})} = \frac{0,99}{0,10} = 9,9.\]

Interpretamos como sendo cerca de 10 vezes mais provável a hipótese “espécie ocorre” do que “espécie não ocorre” quando há detecção.

2.1.2 Inferência bayesiana: o conhecimento a priori importa?

Na abordagem bayesiana, incluímos a probabilidade a priori de ocorrência, \(P(O)\). Quando recebemos a informação de detecção, atualizamos essa probabilidade, tornando-a \(P(O|D)\).

No exemplo, conhecemos:

  1. \(P(O) = 0,05\) e \(P(\overline{O}) = 0,95\);
  2. \(P(D|O) = 0,99\) e \(P(D|\overline{O}) = 0,10\).

Pelo Teorema de Bayes:

\[P(O|D) = \frac{P(O)\,P(D|O)}{P(O)\,P(D|O) + P(\overline{O})\,P(D|\overline{O})}.\]

Substituindo valores:

\[P(O|D) = \frac{0,02 \times 0,99}{0,02 \times 0,99 + 0,98 \times 0,10} \approx 0.17.\]

E:

\[P(\overline{O}|D) = \frac{0,98 \times 0,10}{0,02 \times 0,99 + 0,98 \times 0,10} \approx 0.83.\]

Mesmo com a detecção, a chance de não-ocorrência ainda é maior, favorecendo a hipótese de falso positivo.

2.1.3 Diferenças entre as abordagens

A verossimilhança foca em \(P(D|O)\), enquanto a inferência bayesiana calcula \(P(O|D)\) diretamente, ponderada por \(P(O)\). Se \(P(O) = 0,5\), então:

\[P(O|D) = \frac{0,5 \times 0,99}{0,5 \times 0,99 + 0,5 \times 0,10} \approx 0,91,\] \[P(\overline{O}|D) \approx 0,09,\]

e a razão \(\frac{P(O|D)}{P(\overline{O}|D)}\) será igual a \(RV = 9,9\), tal como na verossimilhança. Porém, quando \(P(O)\) indica uma espécie muito rara, esse valor a priori altera o resultado final de \(P(O|D)\). Por isso, as duas abordagens só coincidem quando usamos uma priori não-informativa (probabilidades iniciais iguais para presença e ausência).