Probabilidade condicional e independência

Probabilidade condicional

Eventos dependentes

Teorema de Bayes

Diagrama de árvore

Exploração da probabilidade condicional e independência, com aplicações do Teorema de Bayes.

Pacotes e funções utilizadas

library(tidyverse)
library(gt)
library(ggVennDiagram)
source("scripts/conditional_tree.r")

1 Probabilidade Condicional

Consideremos o experimento “virar uma estrutura (folha ou galho) e contar o número de itens”:

\(\Omega = \{(F0), (F1), (F2), (F3), (F4), (F5), (F6), (G0), (G1), (G2), (G3), (G4)\}\)

Sejam definidos os eventos:

\(A\): “virar uma folha”:
\[A = \{\text{(F0), (F1), (F2), (F3), (F4), (F5), (F6)}\}.\]
\(B\): “obter 3 ou mais itens”:
\[B = \{\text{(F3), (F4), (F5), (F6), (G3), (G4)}\}.\]

Que podem ser representados no diagrama de Venn:

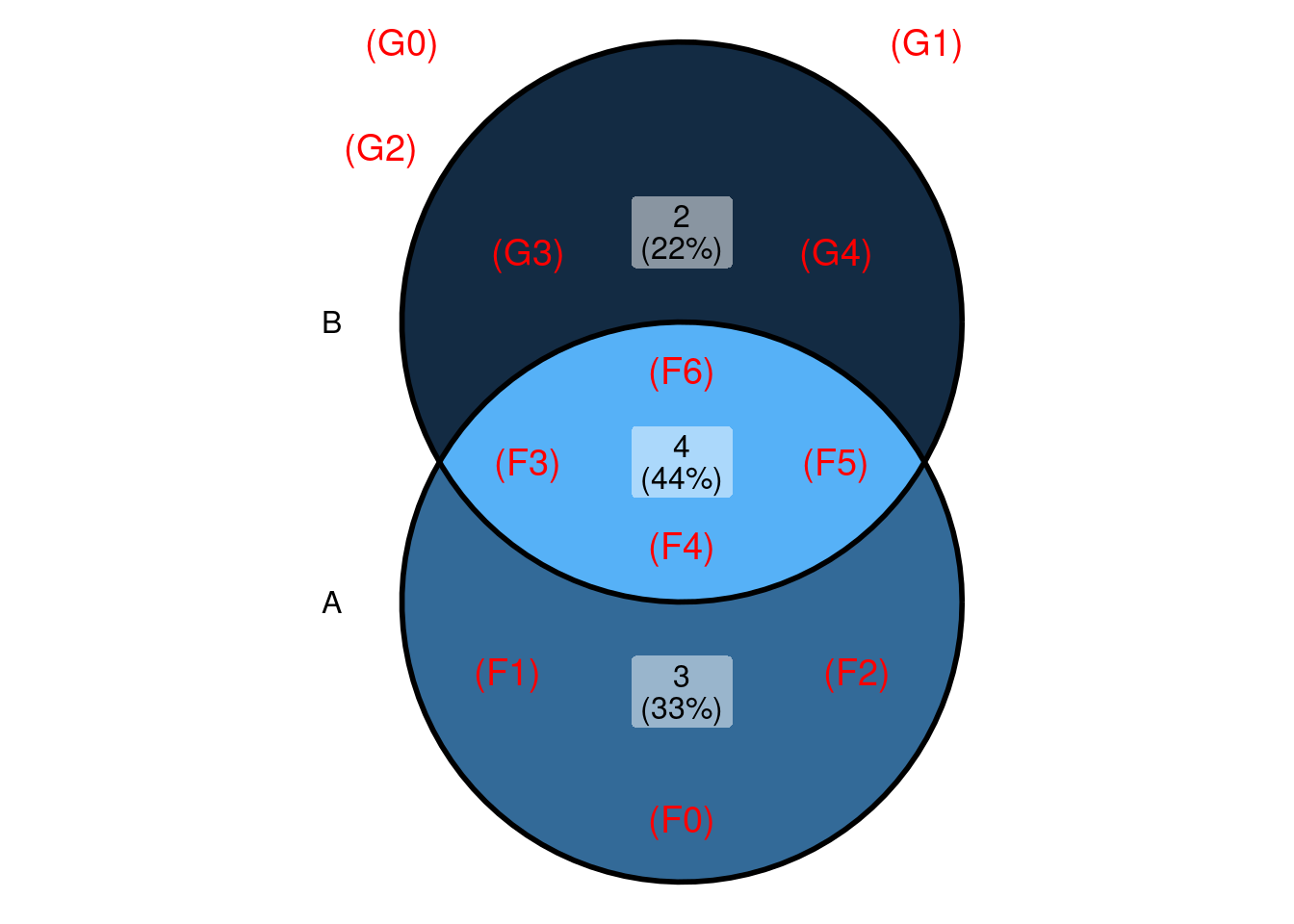
Podemos perguntar:

Considerando que tenha sido virada uma folha, qual a probabilidade de que tenham sido obtidos mais de 3 itens?

Ao informar que a estrutura era uma folha, sabemos que nem todos os eventos de \(\Omega\) podem ter ocorrido. Neste exemplo, somente as 7 observações do evento e \(A\) consistem de uma folha.

Destas, apenas 4 possuem mais de 3 itens, de modo a resposta à pergunta seria \(\frac{4}{7}\). Este resultado é conhecido como probabilidade condicional, denotada pelo símbolo (\(|\)). Neste exemplo específico estamos perguntando:

Dado que \(A\) OCORREU, qual a probabilidade de que \(B\) ocorra? Simbolicamente, esta questão é escrita como \(P(B|A)\) e lida como probabilidade de \(B\) dado \(A\).

\[P(B|A) = \frac{4}{7} = 0.57\]

Esta probabilidade condicional foi calculada pelo número de observações favoráveis à intersecção de \(A\) e \(B\) (\(A \cap B\)) relativa ao número de observações do evento \(A\). Isto significa que ao sabermos parte dos resultados, o espaço amostral inicial foi reduzido, neste caso, ao espaço coincidente com \(A\).

Deste modo, a probabilidade condicional pode ser expressacomo:

\[P(B \mid A) = \frac{P(A \cap B)}{P(A)}\]

que neste exemplo será:

\[P(B \mid A) = \frac{P(A \cap B)}{P(A)} = \frac{4}{7} = 0.57\]

2 Representação de eventos: diagrama de árvore

Quando lidamos com experimentos em etapas ou eventos sequenciais, um diagrama de árvore ajuda a visualizar cada estágio, indicando as probabilidades e as condicionais:

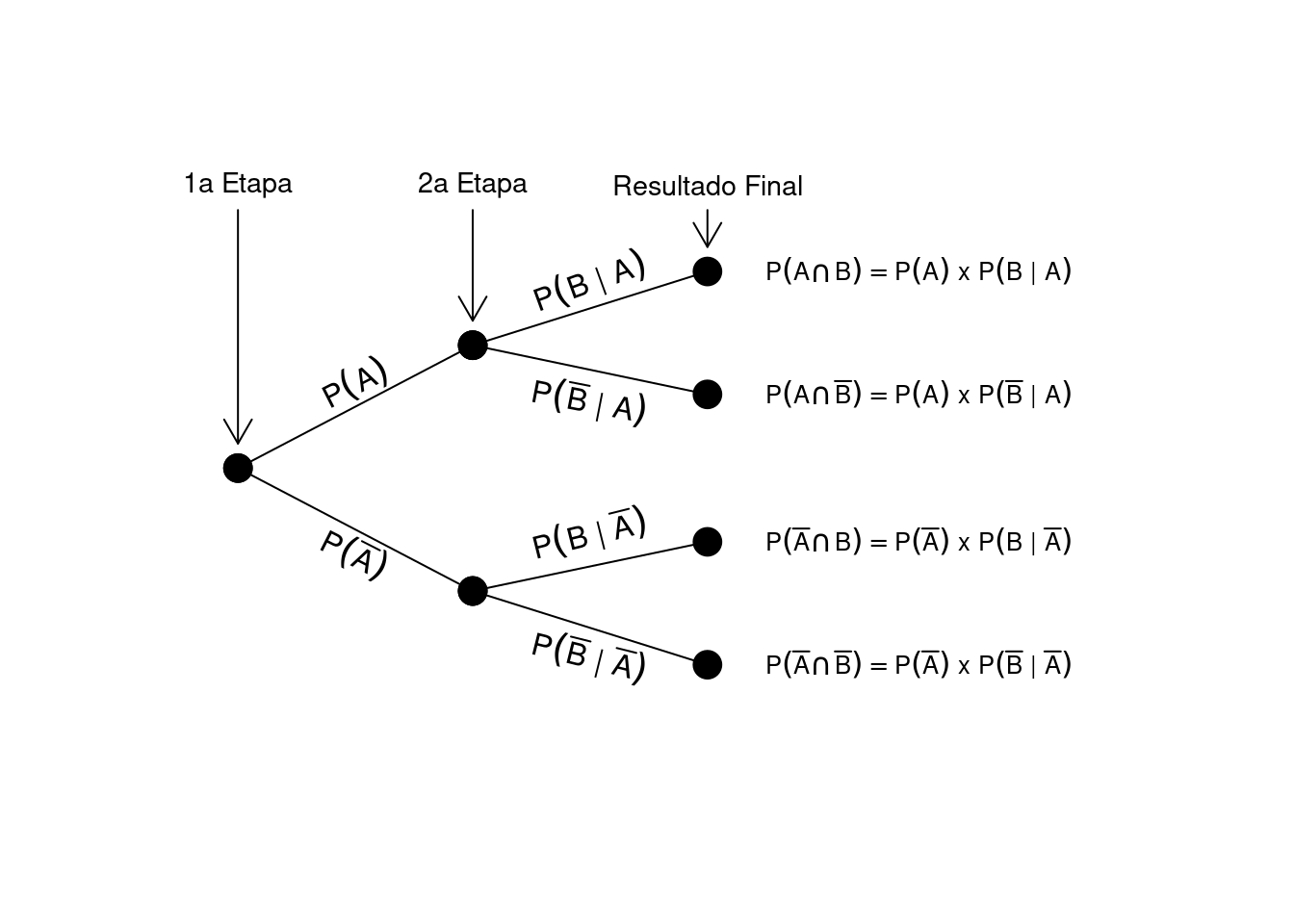
Nesse diagrama, cada ramo representa um cenário: por exemplo, ao ocorrer \(A\), \(B\) pode acontecer com \(P(B \mid A)\), resultando na intersecção \(A \cap B\). Assim, o diagrama possibilita mapear todos os cenários possíveis de maneira organizada.

3 Eventos independentes

Dois eventos \(A\) e \(B\) são independentes quando conhecer a ocorrência de um deles não altera a probabilidade do outro, ou seja, conhecer \(A\) não nos diz nada sobre a probabilidade de ocorrência de \(B\), de modo que \(P(B) = P(B \mid A)\).

No experimento “virar uma estrutura e contar o número de itens”, temos por exemplo.

\(P(B) = 0.5\)

e que

\(P(B \mid A) = 0.57\)

Portanto, ao sabermos que a estrutura virada foi uma folha, a probalidade de que tenham sido observados 3 ou mais items foi alterada.

Os eventos \(A\) e \(B\) são portanto eventos dependentes em que \(P(B) \neq P(B \mid A)\).

3.1 Exemplo de eventos independentes

Suponha que foram investigadas 600 pessoas, classificadas por idade e local de origem. Nesse contexto temos os eventos:

\(A\): ter até 20 anos; \(\overline{A}\): ter mais de 20 anos.
\(B\): ser da cidade; \(\overline{B}\): ser de fora da cidade.

Considere a matriz:

idade	Da cidade	De fora da cidade
Até 20	30	170
Mais de 20	60	340

As probabilidades são:

\(P(A) = \frac{200}{600} = 0.33\)

\(P(\overline{A}) \;=\; \frac{400}{600} = 0.67\)

\(P(B) = \frac{90}{600} = 0.15\)

\(P(\overline{B}) \;=\; \frac{510}{600} = 0.85\)

Sabendo, por exemplo, que a pessoa tem mais de 20 anos, a probabilidade de ela ser da cidade é:

\[P(B \mid A) = \frac{60}{400} = 0.15.\]

Uma vez que \(P(B) = P(B \mid A)\), então \(A\) e \(B\) são eventos independentes.

4 Eventos independentes vs mutuamente exclusivos

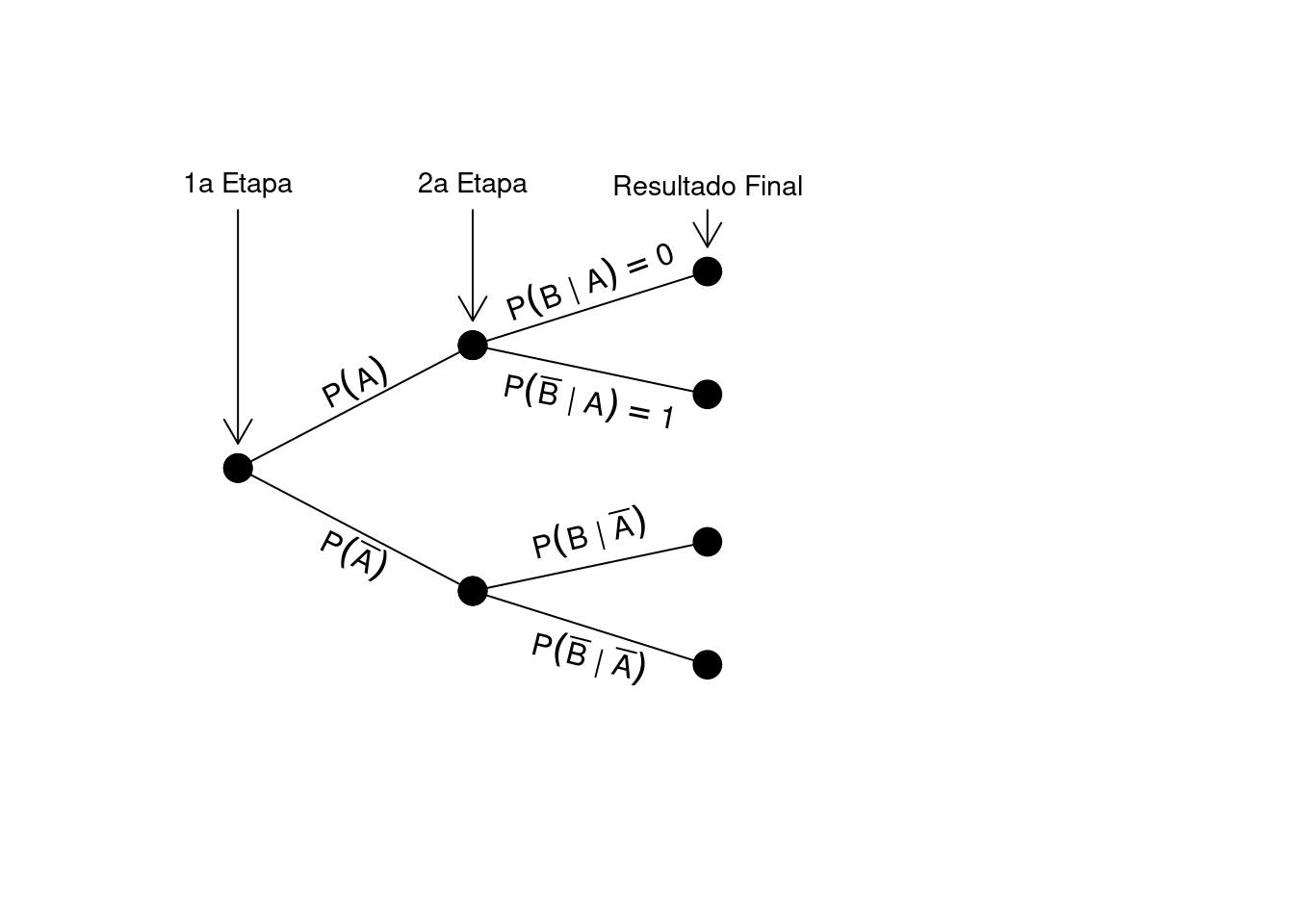
Dois eventos são mutuamente exclusivos quando \(P(A \cap B) = 0\). Se ambos ocorrerem, excluem-se mutuamente. Logo, se \(A\) ocorre, \(B\) não pode ocorrer. Nesse caso, \(P(B \mid A) = 0\), caracterizando dependência, pois a informação de \(A\) determina que \(B\) não ocorrerá.
Dois eventos são independentes se \(P(A \cap B) = P(A)\times P(B)\). Isso significa que conhecer \(A\) não altera a probabilidade de \(B\). Se \(P(A)\) e \(P(B)\) forem não nulos, então não podem ser ao mesmo tempo mutuamente exclusivos e independentes.

A representação de eventos mutuamente exclusivos no diagrama de árvore é ilustrada por \(P(B \mid A)=0\), pois, ao ocorrer \(A\), já se sabe que \(B\) não ocorrerá. Assim, eventos mutuamente exclusivos implica serem eventos dependentes. Se não há exclusividade, os eventos podem ou não ser independentes, dependendo de \(P(B)\) em relação a \(P(B \mid A)\).