Espaço de possibilidades de um experimento

Probabilidade

Espaço amostral

Eventos

Experimento aleatório

Espaço de possibilidades de um experimento aleatório, abordando a definição de evento e probabilidade.

Pacotes e funções utilizadas

library(tidyverse)
library(gt)

Considere uma pesquisa para determinar os locais de ocorrência de uma espécie de peixe endêmica de riachos costeiros de Mata Atlântica no sudeste do Brasil. A pesquisa envolve amostrar trechos de riachos em diferentes bacias hidrográficas da região. Ao amostrar um determinado riacho, o pesquisador não sabe antecipadamente se irá ou não encontrar a espécie. Em probabilidade, chamamos esse ato de experimento aleatório, pois o resultado só é conhecido após a realização.

Embora não saibamos o resultado de um experimento específico, sabemos quais são os resultados possíveis. Neste exemplo, vamos assumir que existem apenas dois resultados para o ato de amostrar um riacho: ou a espécie ocorre, ou não ocorre.

Evento: cada resultado (ocorre ou não-ocorre).
Espaço amostral: conjunto de todas as possibilidades de um experimento. Usualmente denotado por \(\Omega\).

No caso em questão:

\(\Omega = {(ocorre), (não-ocorre)}\)

Definições

Experimento aleatório: aquele cujos possíveis resultados são conhecidos, mas só observados após a realização do experimento.
Espaço amostral: o conjunto de todas as possibilidades de um experimento aleatório.
Evento: cada resultado específico do experimento.

1 Probabilidades de um evento

Mesmo sem saber o resultado de um experimento particular, podemos perguntar sobre a chance de cada evento ocorrer. Em termos probabilísticos, estamos interessados em \(P(ocorre)\). Quando \(P(ocorre) = 0\), significa que a espécie jamais ocorre nos riachos; quando \(P(ocorre) = 1\), significa que a espécie ocorre em todos os riachos. Na prática, a probabilidade ficará entre esses extremos: \(0 \le P(ocorre) \le 1\).

Podemos estimar essa probabilidade empiricamente. Suponha que planejamos amostrar um determinado número de riachos, observando quantas vezes a espécie é capturada.

Digamos que em certo dia foram amostrados 10 riachos e a espécie foi registrada em 4 deles. Nossa estimativa da probabilidade de ocorrência será:

\[P(ocorre) = \frac{\#ocorres}{\#riachos} = \frac{4}{10} = 0.4\]

Naturalmente, como os dois eventos no espaço amostral são \((ocorre)\) e \((não-ocorre)\), a probabilidade de não-ocorrência é:

\[P(não-ocorre) = 1 - \frac{\#não-ocorre}{\#riachos} = 1 - \frac{4}{10} = 0.6\]

e, sendo eventos mutuamente exclusivos e exaustivos (não podem ocorrer juntos e são as únicas possibilidades), temos:

\[P(ocorre) + P(não-ocorre) = 1 = P(\Omega)\]

A probabilidade de não-ocorrência também é conhecida como complemento de \(P(ocorre)\), frequentemente denotado por \(P(\overline{ocorre})\):

\[P(não-ocorre) = P(\overline{ocorre})\]

1.1 Estimando probabilidades

A estimativa acima descreve o resultado para um conjunto fixo de 10 riachos. No entanto, se continuarmos a amostrar novos riachos, essa estimativa pode variar, pois eventualmente encontraremos mais (ou menos) riachos com a espécie presente. Assim, com um número finito de observações, nossa estimativa não será exatamente igual à probabilidade real.

Suponha que repetimos o experimento em 30 riachos. A cada nova amostra coletada, calculamos a fração acumulada de ocorrências:

Observações	Ocorrência acumulada	P(ocorre)
1	0	0.0000000
2	0	0.0000000
3	1	0.3333333
4	1	0.2500000
5	1	0.2000000
6	2	0.3333333
7	2	0.2857143
8	3	0.3750000
9	4	0.4444444
10	4	0.4000000
11	4	0.3636364
12	4	0.3333333
13	4	0.3076923
14	4	0.2857143
15	4	0.2666667
16	5	0.3125000
17	5	0.2941176
18	5	0.2777778
19	5	0.2631579
20	5	0.2500000
21	5	0.2380952
22	5	0.2272727
23	5	0.2173913
24	5	0.2083333
25	5	0.2000000
26	6	0.2307692
27	6	0.2222222
28	6	0.2142857
29	6	0.2068966
30	7	0.2333333

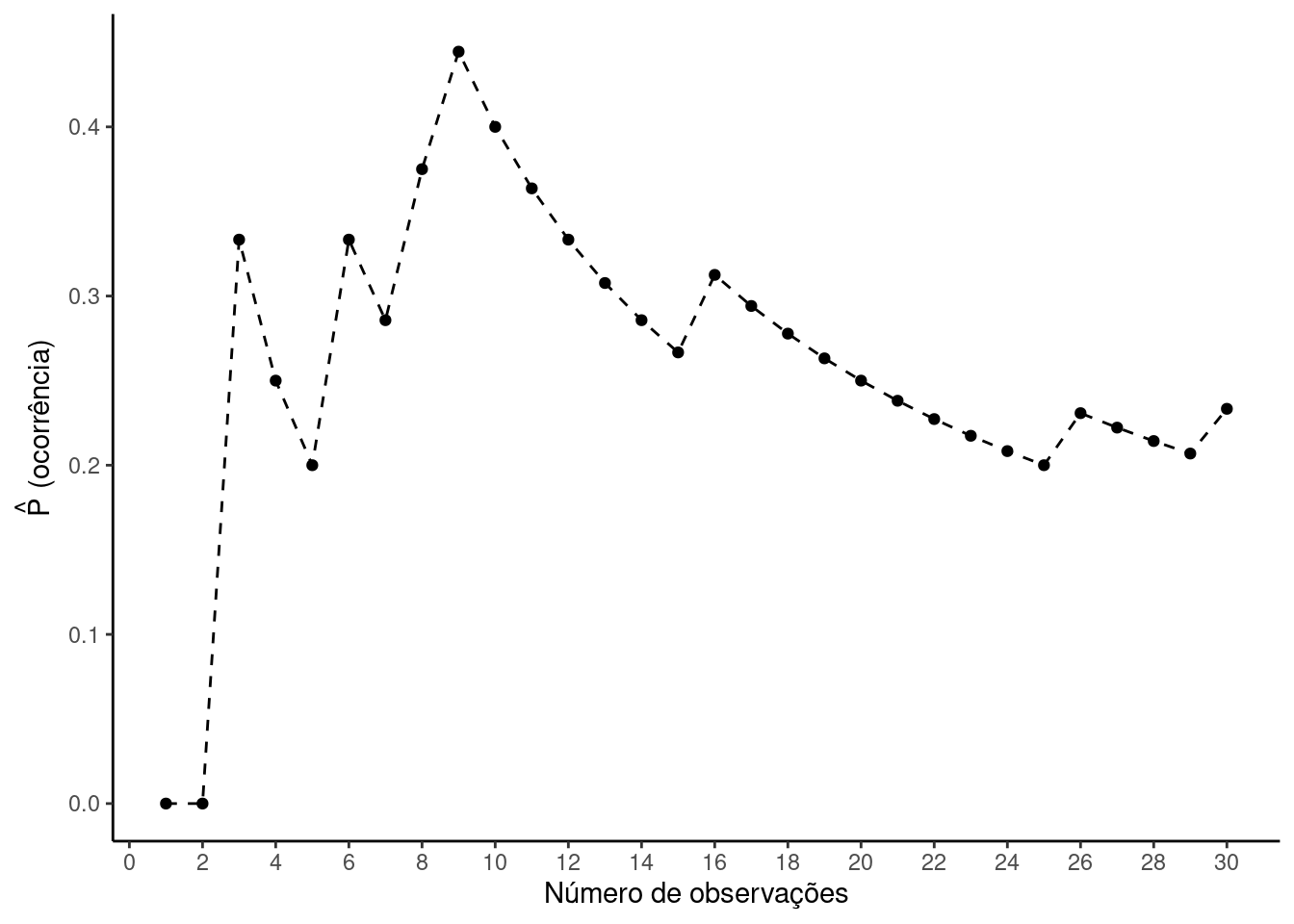
Note como a estimativa de \(P(ocorre)\) oscila. Espera-se que este valor gradualmente aproxime-se para probabilidade real à medida que o número de observações cresce.

Lei dos Grandes Números

A Lei dos Grandes Números afirma que, à medida que o número de repetições de um experimento aleatório cresce, a frequência relativa de um evento tende a se aproximar da probabilidade real desse evento. Portanto, se continuarmos amostrando mais riachos, a proporção de vezes em que a espécie ocorre deve convergir para a probabilidade verdadeira de ocorrência.