Combinando as probabilidades de eventos

Combinação de probabilidades de eventos, utilizando diagramas de Venn e árvores para representar uniões e interseções.

DicaPacotes e funções utilizadas

library(tidyverse)
library(ggVennDiagram)

1 Eventos complexos

Consideremos a seguinte situação: há dois tipos principais de estruturas nas quais um animal aquático pode procurar suas presas: folhas e galhos. As folhas podem conter entre 0 e 6 itens, enquanto os galhos podem conter entre 0 e 4 itens. Ao virar qualquer uma dessas estruturas, o predador consome todos os itens encontrados. Embora seja um exemplo altamente hipotético, ele serve para ilustrar nossa discussão. A pergunta que nos interessa é: ao virar uma dessas estruturas, de quantos itens o predador poderá se alimentar?

Vejamos as possibilidades. Denotemos por \(F\) ou \(G\) o evento de encontrar, respectivamente, uma folha ou um galho, e por \(0\) a \(n\) o número de itens presentes. O espaço amostral do experimento — virar uma estrutura e contar quantos itens há — é dado por:

\[\Omega = \{\text{(F0), (F1), (F2), (F3), (F4), (F5), (F6), (G0), (G1), (G2), (G3), (G4)}\}.\]

Note que há \(\text{12}\) eventos simples e mutuamente exclusivos.

Considere agora o evento \(A\): “virar uma folha”, que ocorre quando observamos F0 ou F1 ou F2 ou F3 ou F4 ou F5 ou F6. Em notação de conjunto:

\[A = \{\text{(F0), (F1), (F2), (F3), (F4), (F5), (F6)}\}.\]

O evento \(A\) é um evento complexo, pois consiste na união de vários eventos simples. Ou seja, podemos dizer que \(A\) acontece se a estrutura virada for uma folha com \(0\) OU \(1\) OU \(2\) OU \(3\) OU \(4\) OU \(5\) OU \(6\) itens. A palavra OU indica que basta qualquer uma dessas possibilidades para o evento ser considerado realizado, o que significa que \(A\) pode ocorrer de 7 maneiras diferentes.

Assim, podemos representar \(A\) pela expressão:

\[A = F0 \cup F1 \cup F2 \cup F3 \cup F4 \cup F5 \cup F6,\]

onde, o símbolo \(\cap\) é sendo lido como OU.

1.1 Representação de eventos: diagrama de Venn

Uma forma de visualizar o espaço amostral e seus eventos é por meio de diagramas de Venn. Para isso, vamos considerar também o evento \(B\): “encontrar mais de 3 itens”, que consiste em:

\[B = \{\text{(F3), (F4), (F5), (F6), (G3), (G4)}\}.\]

Observando \(A\) e \(B\) em um Diagrama de Venn, temos:

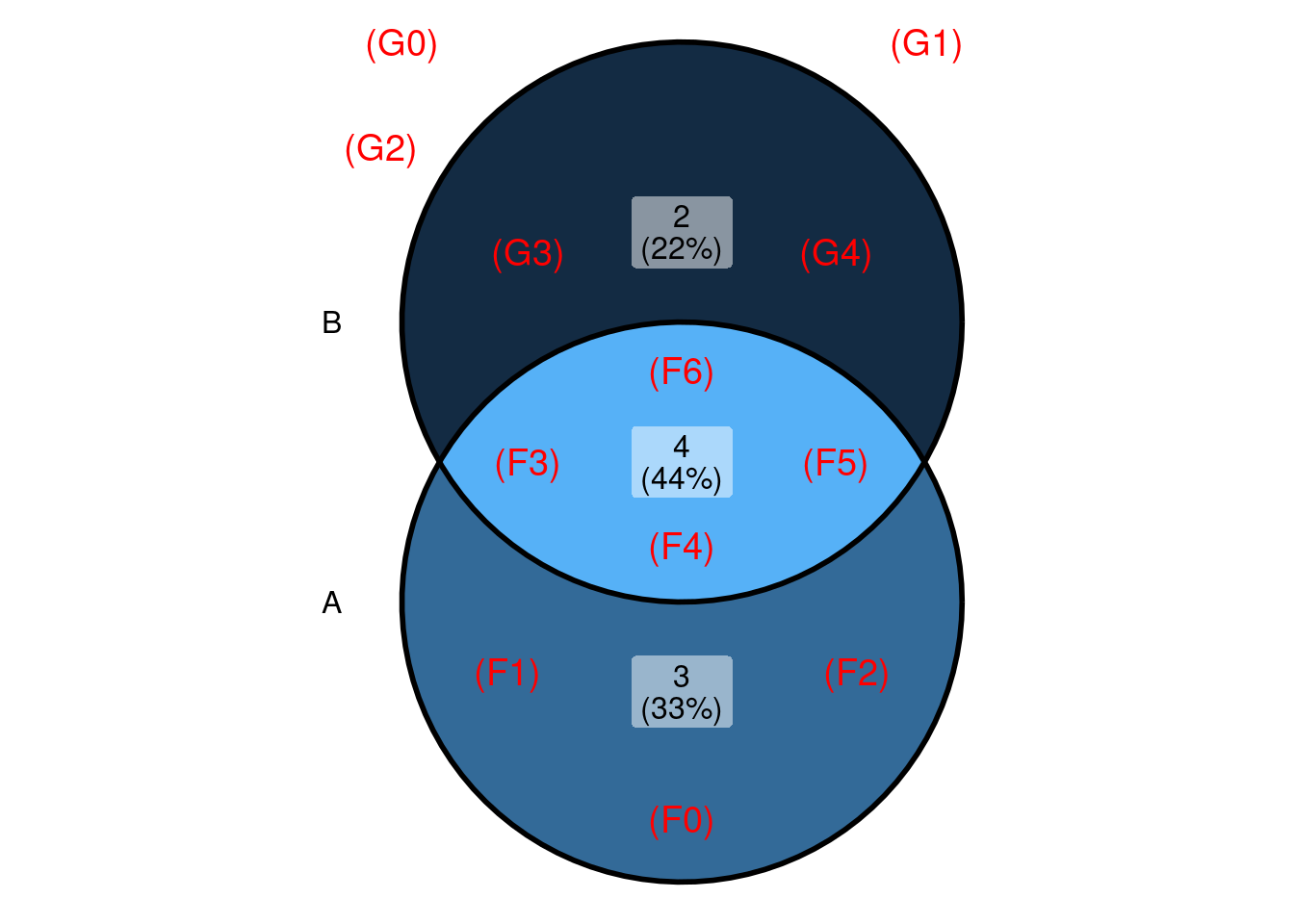
O evento \(B\) também é um evento complexo que ocorre quando se encontra uma folha OU um galho que tenham 3 ou mais itens.

Observe que as ocorrências \((G0)\), \((G1)\) e \((G2)\) não pertencem a \(A\) nem a \(B\), embora façam parte do espaço amostral \(\Omega\).

Considere agora o evento \(C\): “virar uma folha com mais de 3 itens”. Ele pode ocorrer ao observar F3 ou F4 ou F5 ou F6. No diagrama de Venn, vemos que essas possibilidades constituem a intersecção de \(A\) e \(B\) representada por \(\cap\). Portanto, podemos escrever \(C\) como:

\[C = A \cap B.\]

1.2 Probabilidade de eventos complexos

Considerando o experimento virar uma estrutura e contar o número de itens, qual seria a probabilidade de cada observação? Para isso, lembremos que:

1. O espaço amostral consiste em \(N = \text{12}\) observações.

2. Definiremos um modelo de probabilidade para cada uma dessas observações.

Neste tópico, vamos assumir um modelo de probabilidade uniforme, ou seja, cada observação tem a mesma probabilidade \(\frac{1}{N}\).

Dessa forma, a probabilidade do evento \(A\) ocorrer é dada pelo número de resultados favoráveis a \(A\) dividido pelo número total de resultados no espaço amostral. Como \(A\) consiste de 7 observações:

\[P(A) = \frac{7}{12} = 0.58\]

Naturalmente, a probabilidade de \(A\) não ocorrer é:

\[P(\overline{A}) = 1 - \frac{7}{12} = 1 - 0.58 = 0.42\]

O símbolo \(\overline{A}\) representa todas as observações que não pertencem a \(A\).

Considere também a probabilidade de \(B\) que consiste de 6 observações:

\[P(B) = \frac{6}{12} = 0.5\]

Vemos também que o evento \(C = A \cap B\), consiste de 4 observações e portanto:

\[P(C) = P(A \cap B) = \frac{4}{12} = 0.33\]

1.3 Probabilidade da união de eventos

O evento \(A \cup B\) consiste em todas as observações que estejam em \(A\) ou \(B\):

\(A \cup B = \{(F0),(F1),(F2),(F3),(F4),(F5),(F6),(G3),(G4) \}\)

Há 9 ocorrências em \(A \cup B\), de modo que:

\[P(A \cup B) = \frac{9}{12} = 0.75\]

Do diagrama de Venn, fica fácil verificar que o número de eventos em \(A \cup B\) pode ser obtido pelo número de eventos em \(A\) somados ao número de eventos em \(B\) e subtraído pelo número de evendos que ocorrem em ambos (\(A \cap B\)).

Assim:

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

\[P(A \cup B) = 0.58 + 0.5 - 0.33 = 0.75\]