Medidas de posição: quartis

R
Análise de dados
Estatística descritiva
Variabilidade de dados
Análise de dispersão
Cálculo e interpretação de quartis para análise de distribuição, ressaltando faixas de variação e valores atípicos. 
library(tidyverse)
library(gt)
library(patchwork)
source('scripts/assimetria_ggplot.r')

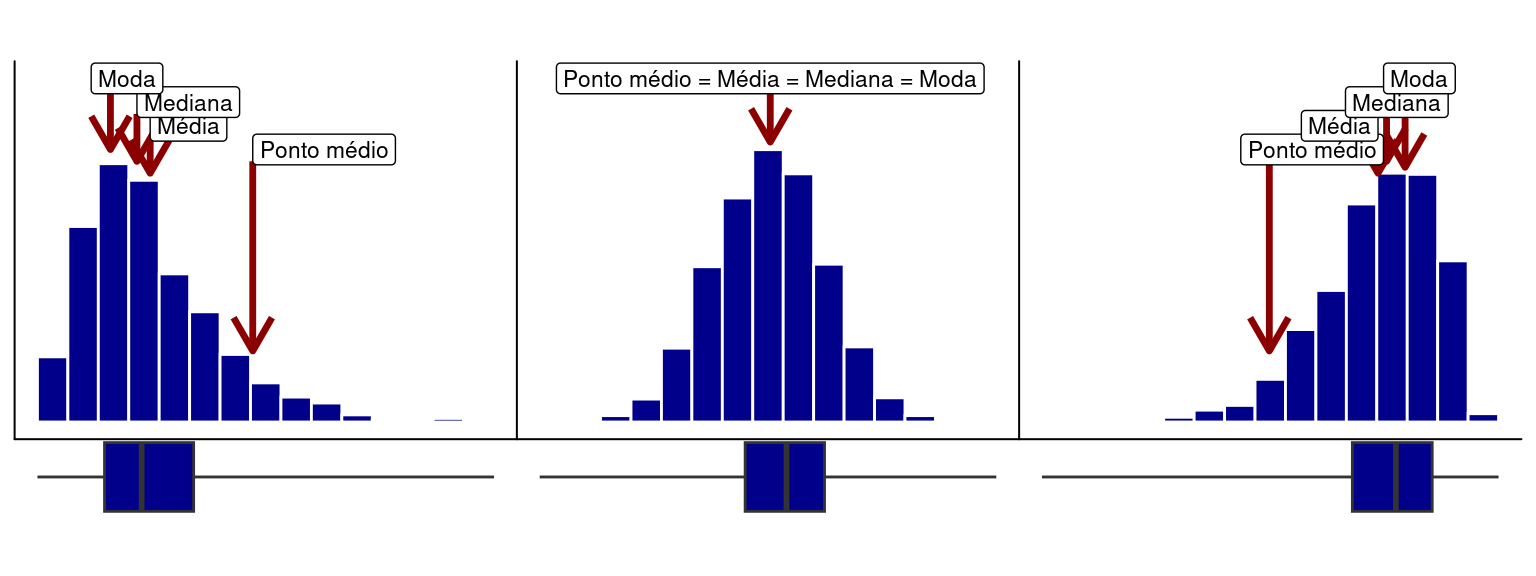
A média, mediana, moda e ponto médio são um tipo de medidas de posição que indicam uma posição particular, isto é, a posição central ao redor da qual os dados estão dispersos. Existem, no entanto, outras medidas de posição como quartis, comumente utilizadas na descrição, análise e interpretação de dados.

Os quartis de uma distribuição de valores são obtidos após ordenarmos os dados em ordem crescente e, em seguida, agrupá-los em partes iguais, contendo cada uma 25% do número total de observações. Se temos 20 observações, cada parte conterá, portanto, cinco observações, \(20 \times 0.25 = 5\). Os quartis são as posições numéricas que dividem estas partes.

Os quartis podem ser indicados por \(Q_1\), \(Q_2\) e \(Q_3\), conforme a figura abaixo.

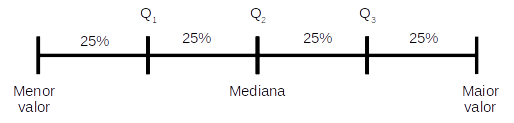
Figura 1: Divisão de uma distribuição de valores em quartis.
NotaQuartis

\(Q_{1}\): O ponto que separa os 25% menores valores do restante da distribuição.

\(Q_{2}\): O ponto que separa os 50% menores valores dos 50% maiores. Este coincide com a Mediana apresentada anteriormente.

\(Q_{3}\): O ponto que separa os 25% maiores valores do restante da distribuição.

Os quartis que veremos aqui são medidas empíricas dos limites indicados na figura acima. Calculamos estes limites a partir de uma amostra de tamanho \(n\).

1 Cálculo dos quartis na posição \(j\)

Existem diferentes algoritmos possíveis para o cálculo dos quartis. Veremos um deles. Para isso, siga os passos abaixo:

  1. Reorganize \(X\) em ordem crescente de \(k = 1\) a \(k = n\). Seja \(n\) o número de observações em \(X\), teremos, portanto, \(X_k\) como o valor observado na posição \(k\) em ordem crescente. Deste modo, para \(k = 1\), teremos \(X_1\) como o menor valor, e para \(k = n\), teremos \(X_n\) como o maior valor.

  2. Calcule

\[L = \frac{j \times (n+1)}{4};\]

  1. Defina \(k\) como o maior número inteiro abaixo de \(L\);

  2. Calcule

\[Q_j = X_k + (L - k) \times (X_{k+1}-X_k);\]

  1. \(Q_j\) será um elemento entre \(X_k\) e \(X_{k+1}\). Se \(X_k\) for um número inteiro, \(Q_j = X_k\).

Exemplo para o cálculo de \(Q_1\)

set.seed(1)
X <- round(rnorm(20, 10, 2), 1)
nX <- length(X)

Considere a variável \(X\) com \(n =\) 20 observações.

\(X\) = 8.7, 10.4, 8.3, 13.2, 10.7, 8.4, 11, 11.5, 11.2, 9.4, 13, 10.8, 8.8, 5.6, 12.2, 9.9, 10, 11.9, 11.6, 11.2

sX <- sort(X)

j1 <- 1
L1 <- j1 * (nX + 1) / 4
k1 <- floor(L1)
Q1 <- sX[k1] + (L1 - k1) * (sX[k1+1] - sX[k1])

j2 <- 2
L2 <- j2 * (nX + 1) / 4
k2 <- floor(L2)
Q2 <- sX[k2] + (L2 - k2) * (sX[k2+1] - sX[k2])

j3 <- 3
L3 <- j3 * (nX + 1) / 4
k3 <- floor(L3)
Q3 <- sX[k3] + (L3 - k3) * (sX[k3+1] - sX[k3])
  1. Organize em ordem crescente para determinar os valores de \(X\) nas posições \(k\).
Posicao_k <- paste(1:length(X), "a Posição", sep = "")
df <- tibble(`Posição k` = Posicao_k, `X ordenado` = sX)

df |> 
  gt()
Posição k X ordenado
1a Posição 5.6
2a Posição 8.3
3a Posição 8.4
4a Posição 8.7
5a Posição 8.8
6a Posição 9.4
7a Posição 9.9
8a Posição 10.0
9a Posição 10.4
10a Posição 10.7
11a Posição 10.8
12a Posição 11.0
13a Posição 11.2
14a Posição 11.2
15a Posição 11.5
16a Posição 11.6
17a Posição 11.9
18a Posição 12.2
19a Posição 13.0
20a Posição 13.2
  1. Para \(j = 1\) (\(Q_1\)), calcule:

\(L = \frac{1 \times (20+1)}{4} = 5.25\);

  1. Defina \(k\) como o maior número inteiro abaixo de \(L\). Portanto, se \(L = 5.25\), \(k = 5\).

  2. Note que a observação correspondente à \(k = 5\) (5\(^a\) posição) é 8.8, enquanto a observação correspondente à \(k = 6\) (6\(^a\) posição) é 9.4. Deste modo, calcule

\(Q_1 = 8.8 + (5.25 - 5) \times (9.4 - 8.8) = 8.95\).

Vemos então que, para a variável \(X\) em questão, o primeiro quartil é:

\(Q_1 = 8.95\)

Exercício: Calcule agora os valores correspondentes a \(Q_2\) e \(Q_3\) e verifique que os resultados são: \(Q_2 = 10.75\) e \(Q_3 = 11.575\).

2 Cálculo dos quartis no R

Podemos programar a sequência de funções acima utilizando o R:

X <- c(8.7, 10.4, 8.3, 13.2, 10.7, 8.4, 11, 11.5, 11.2, 9.4, 
       13, 10.8, 8.8, 5.6, 12.2, 9.9, 10, 11.9, 11.6, 11.2)

# Ordenando X em ordem crescente
sX <- sort(X, decreasing = FALSE)
# Encontrando o número de observações em X
n <- length(X) 
# Encontrando os quartis (Q1, Q2 e Q3)
j <- c(1, 2, 3)
L <- j * (n + 1) / 4
k <- floor(L)
Q <- sX[k] + (L - k) * (sX[k+1] - sX[k])
names(Q) <- c('Q1', 'Q2', 'Q3')

# Visualizando os quartis
Q
    Q1     Q2     Q3 
 8.950 10.750 11.575

Entretanto, existe uma função no R denominada quantile, que pode ser utilizada da seguinte forma:

quantile(X, probs = c(0.25, 0.50, 0.75))
   25%    50%    75% 
 9.250 10.750 11.525
NotaObservações

  • Lembre que o quartil \(Q_1\) delimita a posição \(25\%\), \(Q_2\) delimita a posição \(50\%\) (\(=\) mediana) e \(Q_3\) delimita a posição \(75\%\). Por este motivo, utilizamos o argumento probs = c(0.25, 0.50, 0.75). Assim, a função quantile é mais geral que a rotina passada anteriormente, pois permite o cálculo para qualquer posição entre os quantis \(0\%\) e \(100\%\).

  • Note também que os resultados foram ligeiramente diferentes, uma vez que existem diferentes algoritmos para o cálculo dos quartis. A função quantile permite a escolha entre \(9\) algoritmos diferentes e, por padrão, utiliza o type = 7. O passo-a-passo que mostramos corresponde ao type = 6. Você pode verificar que, ao digitar o comando abaixo, os resultados serão os mesmos que calculamos manualmente.

quantile(X, probs = c(0.25, 0.50, 0.75), type = 6)
   25%    50%    75% 
 8.950 10.750 11.575

  • Essas diferenças diminuem à medida que o tamanho amostral aumenta.

  • Finalmente, os quartis discutidos aqui são casos particulares de limites mais gerais denominados quantis, que indicam uma posição específica na distribuição. Por exemplo, o limite \(Q_1\) poderia ser chamado de Quantil \(0,25\). Assim, podemos encontrar qualquer posição, como o quantil \(0,10\) que delimita os \(10\%\) menores valores.

  • No cálculo dos quantis para um limite \(p\) qualquer (\(0 \le p \le 1\)), a única mudança no algoritmo apresentado está na obtenção de \(L\) (passo 2), que é feita como:

\[L = p \times (n+1)\]

3 Obtendo os quartis a partir de uma tabela de dados

Importe a base de dados Reservatorios_Parana_parcial.csv.

res <- read_delim(
  file = "https://raw.githubusercontent.com/FCopf/datasets/refs/heads/main/Reservatorios_Parana_parcial.csv",
  delim = ",",
  locale = locale(decimal_mark = ".", encoding = "latin1")
)

Usaremos a função summarise para obter os quartis para a variável CPUE.

res |> 
  reframe(Quartis = quantile(CPUE, probs = c(0.25, 0.50, 0.75)),
          Limites = c('25%', '50%', '75%')) |> 
  gt()
Quartis Limites
7.43 25%
11.74 50%
16.30 75%

4 Boxplots: uma representação gráfica dos quartis

Os quartis de uma distribuição nos ajudam a entender o formato de uma distribuição. Uma das formas amplamente estabelecidas de representá-los graficamente é por meio de um boxplot. Para a variável acima, o boxplot será:

Código 
df <- data.frame(X)
PX <- quantile(X, probs = c(0, 0.25, 0.50, 0.75, 1))
LegX <- c("Mínimo", "Q1", "Q2 = Mediana", "Q3", "Máximo")
ggplot(df, aes(y = X)) +
  geom_boxplot(fill = 'lightblue', coef = 10) +
  annotate(geom = 'text', x = .8, y = PX - 0.3,
           label = LegX) +
  annotate(geom = 'segment', 
           x = 0.5, xend = 1.23,
           y = PX, yend = PX,
           arrow = arrow(ends = 'first')) +
  scale_y_continuous(breaks = 5:14) +
  theme_classic() +
  theme(axis.title = element_blank(),
        axis.text.x = element_blank(),
        axis.ticks.x = element_blank())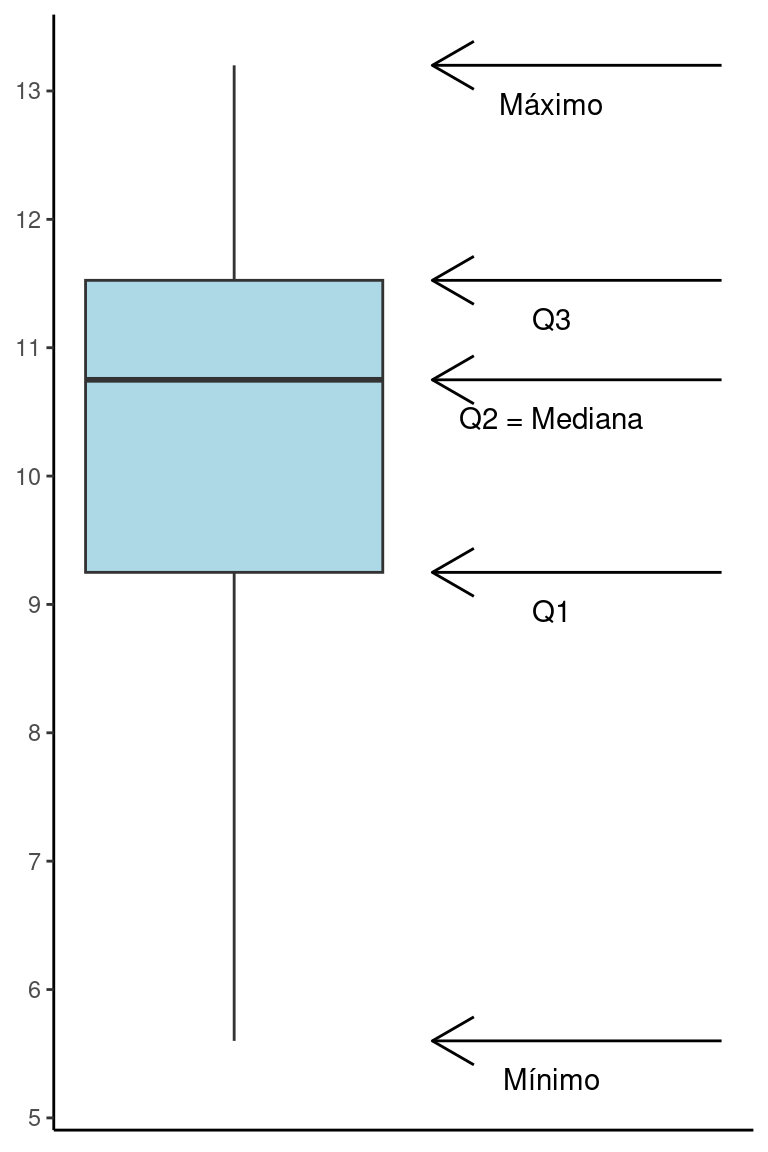
Figura 2: Divisão em quartis de um boxplot

Em um boxplot, a linha central representa a Mediana ou \(2^o\) quartil (\(Q_2\)), e os limites da caixa são o \(1^o\) e \(3^o\) quartis, respectivamente \(Q_1\) e \(Q_3\). As extremidades geralmente são os pontos máximo e mínimo da distribuição.

Existe uma relação entre os histogramas e os boxplots. Ambos podem ser utilizados para avaliar o grau de assimetria de uma distribuição, como apresentado abaixo. Em uma distribuição simétrica, a caixa do boxplot tende a se concentrar no meio da distribuição. Já em distribuições assimétricas, a caixa tende a ficar deslocada à esquerda ou à direita (Figura 3).

Código 
# Ver função completa no arquivo 'scripts/assimetria_ggplot.r'
assimetria_ggplot(fig = 'bh')
Figura 3: Padrão de assimetria representado por meio de histogramas e boxplots.