Medidas de posição: transformação Z

R
Análise de dados
Estatística descritiva
Padronização de dados
Índice Z
Transformação Z para padronizar distribuições, facilitando comparações entre diferentes escalas de medida. 
library(tidyverse)
library(gt)
library(patchwork)
source('scripts/normal_empirica_gg.r')

O índice (ou escore) \(Z\) indica a posição de uma observação particular (\(X_i\)) dentro de uma distribuição, relacionando a posição de \(X_i\) com a média e o desvio padrão da distribuição de \(X\). Suponha uma variável com média \(\overline{X}\) e desvio padrão \(s\). O índice de \(Z_i\) para uma observação \(i\) particular é calculado por:

\[Z_i = \frac{X_i - \overline{X}}{s}\]

Seja, por exemplo, a variável \(X\):

Código 
set.seed(1)
X <- round(rnorm(20, 10, 2), 1)
nX <- length(X)
sX <- sort(X)

\(X\) = 8.7, 10.4, 8.3, 13.2, 10.7, 8.4, 11, 11.5, 11.2, 9.4, 13, 10.8, 8.8, 5.6, 12.2, 9.9, 10, 11.9, 11.6, 11.2

Com média e desvio padrão \(\overline{X} = 10.39\) e \(s = 1.82\), respectivamente.

O índice \(Z_i\) para a \(3a\) observação \(X_{3} = 8.3\) pode ser obtido por:

Código 
i <- 3
Xm <- mean(X)
Xsd <- sd(X)
Zi <- (X[i] - Xm) / Xsd

\(Z_8.3 = \frac{8.3 - 10.39}{1.82} = -1.15\)

1 Interpretando o valor de \(Z\)

O cálculo do índice \(Z\) passa pela centralização e padronização da variável \(X\):

  1. Centralização: a porção \(X_i - \overline{X}\) mede o desvio de cada observação, isto é, a distância (positiva ou negativa) entre \(X_i\) e \(\overline{X}\). O termo centralização refere-se ao comportamento dos desvios estarem distribuídos ao redor de zero, isto é, a média dos desvios é zero.

\[\sum_{i=1}^{n}\frac{(X_i - \overline{X})}{n} = 0\]

  1. Padronização: ao dividirmos a quantia \(X_i - \overline{X}\) pelo desvio padrão de \(X\), obtemos a nova variável denominada \(Z\). O termo padronização refere-se ao fato de o desvio padrão de \(Z\) ser igual a \(1\).

A transformação \(Z\) consiste, portanto, em gerar uma nova variável com média \(\overline{Z} = 0\) e desvio padrão \(s_{Z} = 1\).

Deste modo, o valor de \(Z_i\) associado a uma observação \(X_i\) particular nos indica quantos desvios padrões \(X_i\) está acima ou abaixo da média de seu grupo.

NotaRelação \(Z\) e \(X\)
  • Se \(Z_i = 0\), então \(X_i = \overline{X}\);
  • Se \(Z_i > 0\), então \(X_i > \overline{X}\);
  • Se \(Z_i < 0\), então \(X_i < \overline{X}\);

Para uma distribuição com média igual a \(10\) e desvio padrão igual a \(3\), por exemplo, uma observação \(X_i = 16\) terá um valor de \(Z = \frac{16-10}{3} = 2\), indicando que está dois desvios padrões acima da média de \(X\).

2 Cálculo de \(Z\) no ambiente R

Seja:

Código 
set.seed(1)
X <- round(rnorm(20, 10, 2), 1)

\(X\) = 8.7, 10.4, 8.3, 13.2, 10.7, 8.4, 11, 11.5, 11.2, 9.4, 13, 10.8, 8.8, 5.6, 12.2, 9.9, 10, 11.9, 11.6, 11.2

\(Z\) pode ser obtido pelos comandos:

Xm <- mean(X)
Xsd <- sd(X)
Z <- (sort(X) - Xm) / Xsd

Podemos ver na Tabela 1 os valores de cada observação \(X_i\) e dos respectivos valores de \(Z_i\) em ordem crescente.

Código 
Posicao_k <- paste(1:length(X), "a Posição", sep = "")
df <- tibble(`Posicao k` = Posicao_k, `X ordenado` = sX, Z = round(Z, 2)) |>
  add_row(
    `Posicao k` = c("Média", "Desvio padrão"),
    `X ordenado` = c(round(mean(sX), 2), round(sd(sX), 2)),
    Z = c(round(mean(Z), 2), round(sd(Z), 2))
  )

df |>
  gt()
Tabela 1: Associação entre uma distribuição X e a transformação Z.
Posicao k X ordenado Z
1a Posição 5.60 -2.63
2a Posição 8.30 -1.15
3a Posição 8.40 -1.09
4a Posição 8.70 -0.93
5a Posição 8.80 -0.87
6a Posição 9.40 -0.54
7a Posição 9.90 -0.27
8a Posição 10.00 -0.21
9a Posição 10.40 0.01
10a Posição 10.70 0.17
11a Posição 10.80 0.23
12a Posição 11.00 0.34
13a Posição 11.20 0.45
14a Posição 11.20 0.45
15a Posição 11.50 0.61
16a Posição 11.60 0.66
17a Posição 11.90 0.83
18a Posição 12.20 0.99
19a Posição 13.00 1.43
20a Posição 13.20 1.54
Média 10.39 0.00
Desvio padrão 1.82 1.00

Podemos comparar graficamente as distribuições das variáveis \(X\) e \(Z\).

Código 
hX <- ggplot(df, aes(x = `X ordenado`)) +
  geom_histogram(fill = 'darkblue', color = 'white', bins = 9) +
  ylab('Frequência') +
  scale_x_continuous(n.breaks = 7) +
  theme_classic(base_size = 20)

hZ <- ggplot(df, aes(x = Z)) +
  geom_histogram(fill = 'darkblue', color = 'white', bins = 9) +
  ylab('Frequência') +
  scale_x_continuous(n.breaks = 7) +
  theme_classic(base_size = 20)

hX / hZ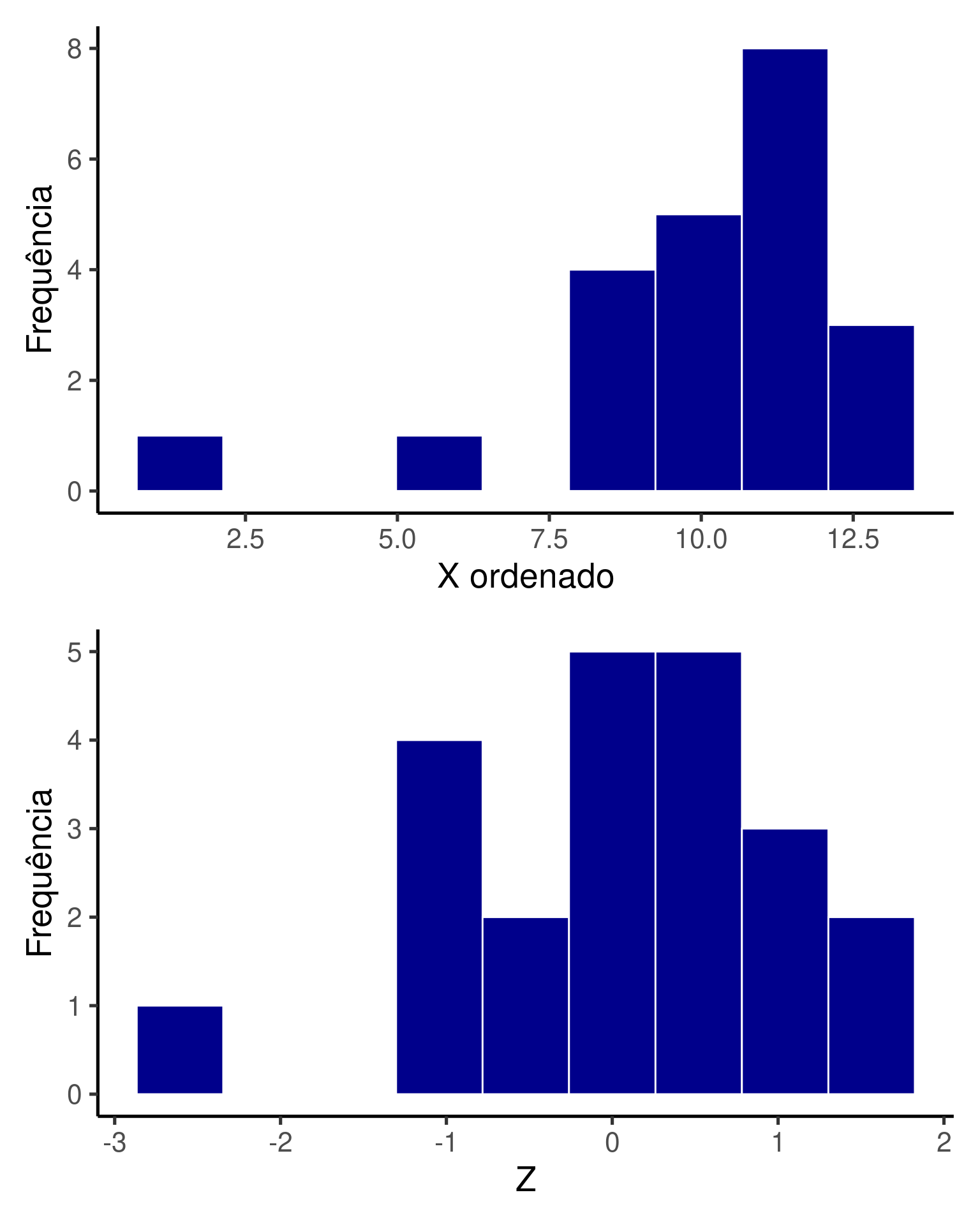
Figura 1: Histogramas representando a distribuição de X e Z.

Veja na Tabela 1 que conforme o valor de \(X_i\) se distancia da média de \(X = 10.39\), mais distante de zero será o valor de \(Z_i\). Neste exemplo, as observações mais extremas de \(X\) estão, respectivamente, a -2.63 desvios padrões abaixo e 1.54 desvios padrões acima da média. Como discutido acima, a nova variável \(Z\) tem média \(\overline{Z} = 0\) (está centralizada) e desvio padrão \(s_Z = 1\) (está padronizada).

3 Obtendo a transformação \(Z\) a partir de uma tabela de dados

Importe a base de dados Reservatorios_Parana_parcial.csv.

res <- read_delim(
  file = "https://raw.githubusercontent.com/FCopf/datasets/refs/heads/main/Reservatorios_Parana_parcial.csv",
  delim = ",",
  locale = locale(decimal_mark = ".", encoding = "latin1")
)

Utilizando a função mutate, vamos manter somente a variável CPUE e criar outra coluna denominada CPUE_z.

df_z <- res |> 
  select(CPUE) |> 
  mutate(CPUE_z = (CPUE - mean(CPUE)) / sd(CPUE)) |> 
  round(2)

df_z |> 
  gt()
CPUE CPUE_z
9.22 -0.47
28.73 2.17
11.59 -0.15
30.76 2.45
5.95 -0.92
7.75 -0.67
7.51 -0.70
4.01 -1.18
20.83 1.10
2.43 -1.39
12.55 -0.02
11.73 -0.13
13.72 0.14
16.50 0.52
4.71 -1.08
7.95 -0.64
13.12 0.06
16.10 0.46
11.74 -0.13
17.95 0.71
13.86 0.16
13.04 0.05
7.35 -0.73
20.92 1.12
13.67 0.13
21.82 1.24
6.29 -0.87
9.40 -0.45
5.60 -0.96
2.05 -1.45
24.88 1.65

Se calcularmos a média e o desvio padrão das variáveis, veremos que CPUE mantém os valores originais, enquanto CPUE_z terá média igual a \(0\) e desvio padrão igual a \(1\).

df_z |> 
  summarize(CPUE_media = mean(CPUE),
            CPUE_dp = sd(CPUE),
            CPUE_z_media = round(mean(CPUE_z), 2),
            CPUE_z_dp = round(sd(CPUE_z), 2)) |> 
  gt()
CPUE_media CPUE_dp CPUE_z_media CPUE_z_dp
12.70097 7.3701 0 1

4 Valores esperados de \(Z\) em uma distribuição normal padronizada

A interpretação de \(Z\) faz sentido quando desejamos posicionar uma determinada observação \(X_i\) como função da média e desvio padrão de seu grupo. Adicionalmente, se uma variável \(X\) puder ser descrita adequadamente por uma distribuição normal de probabilidades, existe uma regra empírica que permite determinar os percentuais das observações acima e abaixo de limites conhecidos.

Código 
# Ver função completa no arquivo 'scripts/normal_empirica_gg.r'
normal_empirica_gg()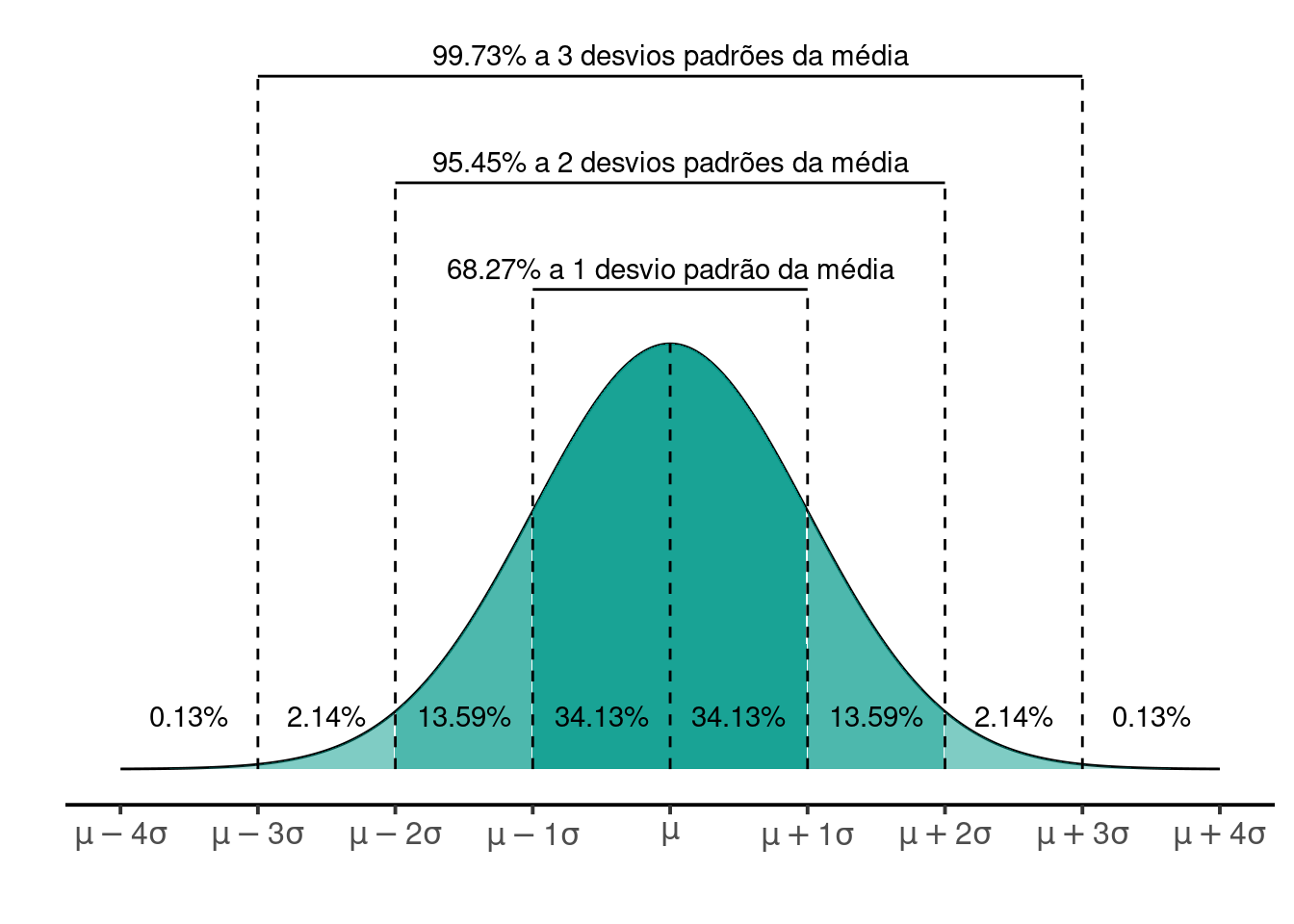
Figura 2: Áreas de probabilidade em uma distribuição normal.

Na Figura 2, vemos que existe uma probabilidade de aproximadamente \(68\%\) de que uma observação tomada ao acaso esteja entre os limites de \(-1\) e \(1\) desvios padrões da média. Existe ainda uma probabilidade de aproximadamente \(95\%\) de que uma observação esteja entre \(-2\) e \(2\) desvios padrões da média. Por outro lado, é muito improvável encontrarmos ao acaso uma observação a mais de \(3\) desvios padrões distantes da média. Isto deverá ocorrer em somente cerca de \(0,26\%\) dos casos em que sortearmos uma amostra aleatoriamente.

NotaUso da distribuição normal empírica

Suponha que a distribuição de altura de homens adultos siga uma distribuição normal com média \(\mu = 175\) cm e desvio padrão \(\sigma = 10\) cm.

Código 
mH <- 175
sdH <- 10
lim <- 2
linf <- round(mH - lim * sdH, 2)
lsup <- round(mH + lim * sdH, 2)

Neste caso, se tomarmos os limites entre \(-2\) e \(+2\) desvios padrões teremos:

\(\mu - 2 \times \sigma = 175 - 2 \times 10 = 155\) cm

e

\(\mu + 2 \times \sigma = 175 + 2 \times 10 = 195\) cm

Estes resultados sugerem que nesta população temos somente cerca de \(5\%\) dos homens adultos com mais de \(195\) cm ou menos de \(155\) cm de altura.